
Информатика
.pdf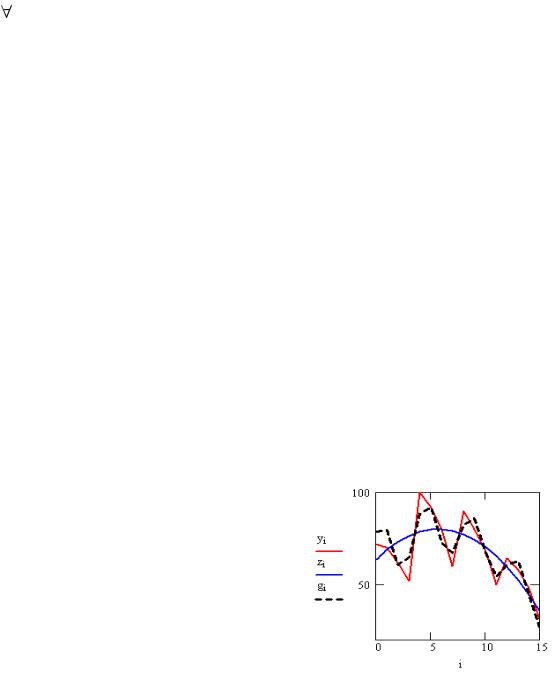
151
n
( k). Чаще рассматривают функцию φ(β) = ∑k=0(f(β, k) - yk)2 и приравнивают ее к нулю в блоке given - minerr. Рассмотрим
Пример 17. Значения некоторой величины, измеренные через равные проме-
жутки времени, имеют вид y := (72 70 62 52 100 92 80 60 90 80 68 50 64 58 48 30)T. Данные носят колебательный характер. Выясним общую тенденцию изменения данных, подобрав параболу f(a, b, c, t) := a + b∙t + c∙t2, наиболее подходящую в смысле МНК: положим n := 15, i := 0..n, определим a := 0, b := 0, c := 0 и введем блок
Given |
|
|
|
|
|
|
|
|
a |
|
a |
63.559 |
|
∑(f(a,b,c,i) - yi) |
2 |
|
:= Minerr(a,b,c) |
|
|
|
= 0 |
b |
b |
= 5.789 |
. |
||
i |
|
c |
|
c |
-0.513 |
|
Получим коэффициенты наилучшей параболы. Вычтем ее из исходных данных, полагая zi := (c∙i + b)∙i +a, ri := yi - zi. В результате останется чисто колебательный процесс с переменной амплитудой. Попробуем этот процесс представить функ-
цией φ(A, s, ω, τ, t) =A∙es∙t∙sin(ω∙t + τ). Возьмем для начала A:= 10, s := -0.5, ω :=
1.5, τ := 1 и введем блок
Given
|
A |
|
∑(φ(A,s,ω,τ,i) - ri)2 = 0 s |
:= Minerr |
|
|
ω |
|
i |
τ |
|
|
|
|
Используя полученные данные, построим окончательную модель y(t) = a + bt + ct2 +
+Aestsin(ωt + τ). Вычислим значения gi := (c∙i + b)∙i + a + A∙est∙sin(ω∙t + τ) и сравним на
графике значения yi, zi, gi (см. рис. 64).
В случае несовместной системы уравнений Minerr возвращает значение, наиболее удовлетворяющее системе (для линейных систем действие аналогично использованию обобщенной обратной матрицы).
Работа с файлами
A 18.252
s -0.043ωτ = 2.161.5 .
Рис. 64
Текстовые файлы (файлы данных)
Функции (записываются через знак присваивания, расширение файла
"prn"):
readprn("путь к файлу") – чтение данных в матрицу из текстового файла,
writeprn("путь к файлу") – запись данных в текстовый файл, appendprn("путь к файлу") – дополнение текстового файла.

152 |
|
|
|
|
1 |
3 |
-5 |
0 |
|
Пример 18. Запишем в текущий каталог матрицу С = 9 |
4 |
2 |
2 |
командой |
6 |
-1 |
4 |
0 |
|
3 |
3 |
-7 |
1 |
writeprn("data.prn"):= C, прочитаем D:= readprn("data.prn"), добавим в файл матрицы строку k := (3 7 2 1) командой appendprn("data.prn"):= k.
Графические файлы
readrgb("путь к файлу") – чтение цветного изображения, readbmp("путь к файлу") – чтение изображения в оттенках серого.
Аналогичны функции для записи изображений. MathCad позволяет редактировать графические файлы, выполнять фильтрацию.
Пример 19. Файл "Ecoinfo.bmp", находящийся в папке "Temp" диска F, содержит текстовую информацию в графическом виде. Часть этого файла представлена рисунком 65 (слева). Прочитаем содержимое файла в массив А командой A := READBMP ("F:\Temp\Ecoinfo.bmp"). Элементы матрицы суть натуральные числа из [0, 255] (0 соответствует черному цвету, 255 белому). Попрбуем сделать изобра-
жение более четким. Положим i:= 0 .. rows(A)-1, j:= 0 .. cols(A)-1, и Bi, j := if(Ai, j < 140, 0, 255). Ниже на рис. 65 приведено исходное изображение (слева) и исправленное (справа), соответствующее в результате такой "фильтрации" матрице В.
Рис. 65
Звуковые файлы (с расширением "wav")
readwav("путь к файлу") – чтение звукового файла в матрицу, writewav("путь к файлу",s,b) – запись в звуковой файл (s – скорость
сэмплов, b – разрешение звука в битах),
getwavinfo("путь к файлу") – создает вектор с информацией о звуковом файле.
В поздних версиях Mcd (13 и далее) имеется встроенный "мастер импорта данных", помогающий в работе с файлами.

153
Программная среда Mсd дает возможность пользователю работать в трех основных режимах:
1.В режиме непосредственного вычисления.
2.В режиме аналитических преобразований.
3.В режиме численного моделирования и программирования.
По поводу непосредственных вычислений сказано достаточно. Режим аналитических преобразований по сути своей не может быть универсален, поэтому так или иначе приходится прибегать к численному моделированию. К этому побуждает и то, что многие встроенные программы и функции имеют ограниченную "связь с внешним миром". Поясним это на примерах.
Пример 20. Для функции f(x) = (x0 - 2)4 +∑3k=1(xk - x 2k-1)2 при начальном значении xk = k, k = 0, ..., 3, попытка найти минимум (очевидно, равный нулю при х = (2,
4, 16, 256)Т) с помощью встроенной функции minimize приводит к результату х = minimize(f,x) = (1.409 1.844 3.362 11.296)T – ничего похожего. Воспользуемся тео-
ремой Ферма и попробуем при тех же условиях найти решение уравнения f '(x) = 0, используя оператор градиента х и блок поска решений Given – Find. Проблема с поиском – решение не найдено. Вычислим, наконец, производную (градиент) непосредственно, вернее, приближенно, кодом:
Df(x) : = ε ← 0.0000001, p ← f(x)
for i 0 .. last(x)
y ← x, yi ← xi + ε di ← (f(y) - p) −: ε
d
Теперь блок Given Df(x) = 0 Find(x)T= (1.918 3.679 13.534 183.172) возвращает результат, намного более точный. Вычисление второй производной (т.е. матрицы Гессе в данном случае) аналитически затруднительно. Но легко воспользоваться приведенным выше кодом, слегка изменив его:
D2f(x) : = ε ← 0.0000001, p ← Df(x)
for i 0 .. last(x)
y ← x, yi ← xi + ε d‹i›← (Df(y) – p) −: ε
d
Если теперь в найденой точке экстремума вычислить A:= D2f(x) и, полагая k:=0..4, вычислить все главные определители матрицы А, получим:
|submatrix(A,0,k,0,k)| = 29.515
3.196∙103
4.618∙106
1.863
154
т.е. все эти определители положительны, по критерию Сильвестра матрица А положительно определена, следовательно, найденная точка – точка минимума.
Здесь снова в целях компактности записи нарушается правило для операторов в Mcd: каждый оператор должен быть записан в отдельной строке (запятые для разделения операторов недопустимы!). В качестве знака деления (с той же целью) использован (допустимый!) символ "−: ", верхний индекс в угловых скобках обозначает столбец матрицы, функция last() возвращает индекс последнего элемента аргумента, функция submatrix(A,i,j,p,q) возвращает подматрицу матрицы А с элементами Au,v, i ≤ u ≤ j, p ≤ v ≤ q, вертикальные скобки возвращают модуль числа, длину вектора или определитель матрицы.
Пример 21. Бесконечные суммы и произведения, в общем, аналитически не вычисляются, несмотря на наличие в Mcd соответствующих операторов. В таких ситуациях требуется программирование (см. примеры 11-13 п. 1.6 и примеры следующих разделов).
6.2. НЕКОТОРЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МОДЕЛИ
Здесь будут рассмотрены некоторые простейшие методы приближенного решения популярных задач в системе Mcd, преследуя две цели:
1)на конкретных примерах научиться программированию;
2)заглянуть в "кухню" алгоритмов, используемых в пакете Mcd, чтобы пользоваться ими сознательно.
6.2.1.Системы уравнений
В общем, в простейшей ситуации здесь можно воспользоваться кнопкой "Solve", блоками Given ... Find, Given ... Minerr, а также функциями Root, Polyroot (для многочленов), Lsolve (для линейных систем уравнений), обратной матрицей, обобщенной обратной матрицей (Geninv), а в случае двух переменных функциями Slope, Intercept.
6.2.1.1.Системы линейных уравнений
Вэтом пункте будет обсуждаться задача решения системы линейных уравнений вида Ax = b, где А – прямоугольная (чаще всего квадратная) матрица, х – искомый вектор, b – вектор (или матрица) правой части. Если А – квадратная невырожденная матрица, а b – вектор,
то задача легко решается либо использованием обратной матрицы (x = A-1b), либо применением встроенной функции lsolve(A, b), возвращающей вектор решения. В противном случае следует использовать специальные методы, выбирающие решение специальным образом.

155
А. Обыкновенная квадратная хорошо обусловленная (определитель матрицы А не слишком мал по сравнению с ее элементами) система уравнений. Ее можно легко решить методом Крамера и методом исключения Гаусса. Программирование метода Крамера довольно очевидно:
Cramer(A, b) := d |A| - 1
for k 0 .. last(b)
‹ k ›
C A, C b
x k |C| ∙ d
x
Приведем также простейший вариант метода Гаусса с выбором диагональных элементов (который используется крайне редко):
Gauss(A,b) : = A ← augment(A,b)T, n ← last(b)
for i 0 .. n
A‹i›← (Ai,i)-1∙A‹i›
for j 0 .. n
A‹j›← A‹j› - Ai,j ∙A‹i› if i ≠ j submatrix(A,n+1,n+1,0,n)T
(сравните с текстом кода в п. 1.7.3 с выбором максимального элемента).
Пример 1. Проверьте, что исключения Гаусса по диагонали не ра-
1 2 3
ботают для системы уравнений с матрицей A= 1 2 4 , det(A) = 5.
4 3 2
Б. Переопределенные системы линейных уравнений полного ранга (ранг матрицы системы равен размерности пространства аргументов) легко решаются методом псевдообратной матрицы (вариант метода наименьших квадратов) с помощью встроенной функции geninv(). В старших версиях Mcd этот метод включен в функцию lsolve, возвращающую как решение, так и псевдорешение системы линейных уравнениы (см. п. 6.1, Векторы, матрицы, СЛАУ).
Если система неполного ранга, решение (или псевдорешение) следует выбирать , исходя из каких-то дополнительных условий. Часто это - требование минимальной нормы решения (близость к началу координат). В этом случае в основу поиска решения кладется комбинация метода исключения Гаусса с выбором главного элемента (см. п. 1.7.3) и метода псевдообратной матрицы: сначала выбирается подсистема полного ранга, далее, если ее ранг равен рангу исходной системы, то находится решение методом исключения, иначе если подсистема переопределена, то находится псевдорешение (geninv), в противном случае – решение с минимальной нормой (см. п. 6.1, СЛАУ).
|
|
|
|
156 |
|
|
Пример 2. Для системы уравнений Aх = b с прямоугольной мат- |
||||||
1 5 |
|
|
|
1 |
|
|
2 4 |
|
|
|
3 |
|
|
рицей A = 3 3 |
|
и правой |
частью b = 2 |
|
функция lsolve(A,b) воз- |
|
4 2 |
|
|
|
-2 |
|
|
|
|
-0.2 |
. Но с транспонированной матрицей А |
|||
вращает псевдорешение |
|
|||||
|
|
0.5 |
|
|
|
|
|
1 2 3 4 |
|
и правой |
3 |
lsolve(A,b) уже не справляется. |
= |
5 4 3 2 |
|
частью b = |
||
|
|
|
1 |
|
Минимальное по (евклидовой) норме решение можно получить, вычи-
-0.233
слив (вручную) псевдообратную матрицу: AT∙(A∙AT)-1∙b = 0.033 .
0.30.567
B. В более сложных ситуациях необходимы специальные приемы. В самом деле, как правило Крамера, так и метод Гаусса для решения системы уравнений с n неизвестными требуют порядка n3 арифметических операций. Для больших систем уравнений это довольно пессимистичная оценка (в задачах экономики решаются системы уравнений с сотнями и тысячами неизвестных). Кроме того, не всегда требуется предельная точность результата. В таких случаях может быть полезен метод итерационного уточнения решения.
Пример 3. Рассмотрим систему линейных уравнений A x=b с
доминирующей главной диагональю, |
т. е. с матрицей А такой, что |
||
|
|
0 при i = j |
|
|Ai, i | > |A i, j|. Введем матрицу Т i, j = |
|
и вектор s i = b i / |
|
|
A i, j / A i, i , i ≠ j |
||
i ≠ j |
|
|
|
A i,i. Тогда систему уравнений можно записать в виде x = s - T x .
Введем в пространстве аргумнтов норму ||x|| = max |xk|. Согласованная
k
с ней норма матрицы имеет вид: ||A|| = max ∑ |Ak,j|. Легко проверить,
k j
что в данном случае ||T|| ≤ δ < 1, так что итерационный процесс уточнения решения x (n + 1) = s - T x (n), x (0) = s, n = 0, 1, ... , будет сходиться к точному решению исходной задачи (метод простых итераций). Действительно, если рассмотреть соответствующую последователь-
ность отклонений ε(k) = x(k+1) – x(k) ( k), то она получается вследствии
итерационного поцесса: ε(n+1) = T∙ε(n) ( n). Переходя к нормам, отсюда
имеем: ||ε(n+1)|| ≤ ||T||∙||ε(n)|| ≤ δ||ε(n)|| ≤ δn||ε(1)|| → 0 (т.е. отклонения
(n→∞)
убывают со скоростью геометрической прогрессии, итерации быстро сходятся к точному решению). На каждой итерации требуется лишь порядка n2 вычислений, так что процесс достаточно экономный. Итерации можно оформить в виде функции:

157
ITER(A, b, e) := n last (b)
for i 0 . . n
r (A i, i ) -1, x i b i ∙ r s i x i , y i 0
for j 0 . . n
T i, j if (i = j, 0, A i, j ∙ r) while |x - y| > e
y x, x s - T y
x
Г. Во многих задачах матрицы линейных систем уравнений оказываются сильно разреженными (бóльшая часть элементов – нули). Эту специфику также можно "употребить во благо". Например, в слу-
чае 3-диагональных систем уравнений (А i,j = 0 при |i - j| > 1) с доминирующей диагональю (|Ai,i| > |Ai,j+1|+|Ai,j-1|) очень эффективен метод "прогонки", использующий лишь эти три диагонали (если ус-
ловие доминирования нарушено, метод может привести к большим вычислительным погрешностям). Будем считать, что система линейных уравнений имеет вид:
a0,1x0 + a0,2x1 = b0 , |
|
|||
|
+ ai,1xi + ai,2xi+1 = bi , 1 i n - 1, |
|
||
|
|
|||
ai,0xi-1 |
|
|||
an,0 xn-1 + an,1 xn = bn. |
|
|||
|
b0 |
a0,2 |
|
|
Положим u0 = |
|
|
, v0 = a0,1 . Тогда из первого уравнения имеем: |
|
a0,1 |
|
|||
x 1 = u 0 - v 0 x 1 . Если уже найдено представление (прямой ход) |
|
|||
xi-1 = ui-1 - vi-1 x i ( i ≥ 1), |
(1) |
|||
то из уравнения ai,0 (ui-1 - vi-1 xi ) + ai,1 xi + a i,2 xi+1 = b i получаем xi = ui - vi xi+1, где теперь
ui = bi - a i,0 ui-1 , vi = |
ai,2 |
|
(i = 1, 2, ...) . |
(2) |
|
ai,1 - ai,0 vi-1 |
|||||
ai,1 - ai,0 vi-1 |
|
|
|||
Тогда из последнего уравнения xn = un, и по формуле (1) получаем x i для всех i = n - 1, n - 2, ... , 1, 0 (обратный ход прогонки). Очевидно, что для хранения значений ui, vi можно использовать измененные xi , bi . Поэтому программа, реализующая процесс прогонки, может быть записана достаточно компактно и просто. С вычислительной точки зрения метод прогонки имеет много очевидных преимуществ перед методом итераций (прямой и обратный ход решают задачу полностью; например, программа легко справляется с системой уравнений с более чем 10000 неизвестных). В Mcd метод можно оформить в виде следующей функции:

158
Prog(A, b) := n Last(b)
x 0 b 0 (A 0, 1) -1, b 0 A 0, 2 (A 0, 1) -1
for i 1 .. n
p (A i, 1 - A i, 0 b i - 1) -1
x i (b i - A i, 0 x i - 1) p, b i A i, 2 p for i n - 1 .. 0
x i x i - b i x i + 1
x
Пример 4. Найдем приближенное решение линейной краевой задачи x(3x2+1)y''(x) + 2y'(x) – 6xy(x) = 4-12x2 на отрезке [1, 2] с усло-
виями у(1) = у(2) = 0. Здесь нетрудно найти точное решение f(x) = 2x - -0.75(x2+1) - 2x1 . Разобьем отрезок [1, 2] на n равных частей с шагом h =
1
n и заменим производные в точках деления приближенными равенст-
вами: y'(xi) ≈ yi+1 - yi-1, y''(xi) ≈ (yi+1 |
- 2yi + yi-1)h-2, где yi = y(xi), xi =1+ |
i |
, i. |
|
n |
||||
2h |
|
|
После приведения подобных членов дифференциальное уравнение превращается в линейную трехдиагональную систему алгебраических уравнений:
(n2xi(3xi2+1)-n) yi-1 - (2n2xi(3xi2+1)-6xi) yi + (n2xi(3xi2+1)+n) yi+1 = 4-12xi2,
i = 1, ..., n - 1, y0 = yn = 0. Несложно проверить, что диагональ матрицы системы доминирующая, поэтому удобно применить метод прогонки.
6.2.1.2. Нелинейные уравнения и системы А. Для одного уравнения на числовой прямой простые итерации
типа xn+1 = f(x n) (n = 0, 1, ... , x 0 – начальное приближение) приводят при n ∞ к решению уравнения x = f(x), если выполнено (достаточное) условие |f ′(x)| M < 1 в некоторой окрестности точного решения.
Уравнение f(x) = 0 всегда можно привести к указанному виду, записав его как x = x + k f(x) (k – параметр релаксации). Тогда итера-
ции xn+1 = xn + k f(xn) (n = 0, 1, 2, …) будут сходиться при условии |1+ k f ′(x)| M < 1 (условие можно выполнить, если в окрестности решения f ′(x) ≠ 0). Можно потребовать на каждом шаге выполнения равенства 1+ k f′(x n) = 0, откуда k=-(f′(xn)) -1 - это метод Ньютона:
xn+1 = xn - (f′(xn))-1 f(xn). Например, m a получается как решение уравнения xm - a = 0 и метод Ньютона здесь приводит к итерациям xn+1 =
(m-1) x n + a x n1 - m, х 0 = 1 (например), которые быстро сходятся к точному
m
решению для произвольного m > 1.

159
В сложных случаях производную можно заменить секущей, пола-
гая k = xn-1 - xn = - (f′( )) -1 для некоторого : (xn - ) ( - xn-1) > 0, f(xn ) - f(xn-1)
что приводит к методу (секущих, квазиньютона):
xn+1 = f(xn) xn-1 - f(xn-1) xn (n = 1, 2, ... ). f(xn) - f(xn-1)
Методы легко программируются. Можно записать реализацию методов релаксации (Relax) и секущих (QuaNew) в виде функций, возвращающих приближенное решение, значение функции на решении и число итераций (точность обоих методов одинакова).
Relax(f, x, k) := n ← 0, t ← x + 1, ε ← 0.000001
while |t - x| >
t ← x, n ← n + 1 x ← t + k f(t)
x
f(x)
n
QuaNew(f, x) := n ← 0, z ← x + 1, ε ← 0.000001
y ← x + 100 , fx ← f(x), fy ← f(y)
while |z - x| >
z ← (fy x - fx y) (fy - fx) -1 x ← y, y ← z, fx ← fy
fy ← f(z), n ← n + 1
z
f(z)
n
Пример 1. Сравним оба метода при поиске решения уравнения ln(x) = (1 + x2) -1, или (1 + x2) ln(x) - 1 = 0, т. е. f(x) = 0, где f(x) = (1 +
x2) ln(x) – |
1, |
и с |
результатом работы блока Given ... Find. Поиск |
|
начинается всюду с точки |
х = 2. Обе программы дают приближенное |
|||
решение |
х =1.4013215 и |
х =1.4013216 со значением функции в |
||
первом случае |
-2.6 10 -7, во втором 2.14 10 -12. Релаксация требует при |
|||
k = - 0.1, -0.3, -0.5 |
n = 27, 7 и 18 итераций. Метод секущих (QuaNew) |
|||
достигает результата за семь итераций. Встроенный блок Given ... Find находит значение х = 1.4013212 со значением функции - 1.169 10 -6.

160
Б. Для нелинейных систем уравнений F(x) = 0 (F: n n ), используя метод Ньютона, аналогично предыдущему получим:
x (n + 1) = x (n) - [DF(x (n))] -1 F(x (n)) , n = 0, 1, ... ,
где DF(x(n)) - матрица частных производных F в точке x (n). Здесь на каждой итерации нужно решать линейную систему уравнений
DF(x(n)) (x(n + 1) – x(n)) = - F(x(n))
относительно вектора s = x(n + 1) – x(n) . Тогда процесс уточнения решения принимает вид (здесь D(f, х) = Df(х)):
Zero(F, D, x, ) := d ← 1
while d >
s ← Lsolve(D(f,x), f(x)) x ← x – s
d ← |s|
x
f(x)
Например, для двух функций с двумя переменными имеем:
f1(x, y)
F(x, y) = ) ,
f2(x, y
|
∂f1(x,y) |
∂f1(x,y) |
|
DF(x, y) = |
∂x |
∂y |
. |
∂f2(x,y) |
∂f2(x,y) |
||
|
∂x |
∂y |
|
Здесть можно использовать меню Анализа (см. рис. 55). При большой размерности пространства проще использовать собственную программу дифференцирования (см. конец п. 6.1).
Пример 2. Рассмотрим систему трех уравнений с тремя неиз-
|
9y2 |
- 16x2 = 7, |
|
|
|
- 9y2 = 5, |
|
вестными |
4z2 |
с отправной точкой x = y = z = 2. |
|
|
|
|
|
|
xy + xz + yz = 1 |
|
|
Положим n = 3 |
i := 0 . . n - 1 x i := 2 , введем вектор-функцию |
||
9 (x1)2 - 16 (x0)2 - 7 f(x) := 4 (x2)2 - 9 (x1)2 - 5
x0 x1 + x0 x2 + x1 x2 - 1
и выполним R := Zero(f, D, x, 10 -6) . Обратим внимание на то, что ре-
зультат R является вектором, компоненты которого (их нельзя назвать "координаты") также векторы. Поэтому непосредственный вывод
{3; 1}
результата в Mсd выглядит так: R = {3; 1} (каждый элемент – мат-
