Момент инерции сплошного цилиндра равен |
|
J 1 mбr 2 . |
(5) |
2
Решая уравнения (1,2,3) находим неизвестное значение Т1, Т2, а.
Ответ: Т1 = 17,6 (Н), Т2 = 13,7 (Н), а = 3,9 м/с2.
5.Для создания «искусственной тяжести» в космическом корабле используется центрифуга с радиусом вращения r = 2 м. Сколько оборотов в минуту (n) должна делать центрифуга, чтобы космонавт испытывал силу реакции опоры в гори-
зонтальном направлении, соответствующую его весу в обычных условиях? Решение. Для выполнения условий задачи на космонавта в центрифуге должна
действовать центробежная сила инерции, равная силе тяжести:
mω2r = mg |
или |
2 |
g |
, |
(1) |
||||
r |
|||||||||
где |
2 n |
|
n |
– угловая скорость; n – число оборотов в минуту. |
|
||||
|
60 |
|
30 |
|
|
|
|
|
|
Отсюда n 30 
gr 21 миноб . Ответ: 21 об/мин.
ЭЛЕКТРОСТАТИКА
6.Два одинаковых маленьких шарика с зарядами 1,8·10-7 Кл и -8·10-8 Кл приведены в соприкосновение и вновь раздвинуты на расстояние 0,5 м. Определить силу взаимодействия между ними.
Дано: q1 =1,8·10-7 Кл q2 =-8·10-8 Кл r=0,5 м
F ?
Решение. После соприкосновения заряды шаров стали равны
между собой, но сумма заряда не изменяется: q3 q1 q2 .
2
Тогда, q3 1,8 10 7 2 8 10 8 5 10 8 Кл.
По закону Кулона сила взаимодействия равна: F |
q2 |
, |
|
3 |
|||
4 0r2 |
|||
|
|
где 0 8,85 10 12 Фм – электрическая постоянная.
41
Получаем, |
F |
|
|
5 10 8 2 |
|
9 10 5 |
H . |
|
3,14 |
8,85 10 12 |
0,5 2 |
||||
|
4 |
|
|
||||
Ответ: F 9 10 5 H .
7.Проволочная прямоугольная рамка со сторонами 20 и 30 см расположена в однородном магнитном поле перпендикулярно к силовым линиям. Опреде-
лите индукцию этого поля, если при его исчезновении за 1,2 10 2 c в рамке
наводится средняя э.д.с. 3,5 мВ. |
|
|
Дано: |
Решение. |
|
a = 0,2 м |
n |
B |
|
||
b = 0,3 м |
|
|
|
|
|
t 1,2 10 2 c |
|
a |
|
|
|
||
i 3,5 10 3 B |
|
|
|
|
|
b |
|
B ? |
|||
|
Рис. 2 |
||
|
|
Э.д.с. индукции равно: i t , где 2 1 – изменение магнитного потока.
При исчезновении поля имеем 2 0, тогда i t1 .
Магнитный поток равен: 1 BS cos , где – угол между векторами n и B ;
S ab – площадь рамки. |
|
|
|
|
|
|
Из рис. 2 видно, что 0. Значит, Bab . Тогда, |
i |
Bab |
B |
i t . |
||
|
|
1 |
t |
|
ab |
|
Получаем, B 3,5 10 3 |
1,2 10 2 |
7 10 4Тл. |
|
|
|
|
0,2 |
0,3 |
|
|
|
|
|
Ответ: B 7 10 4Тл .
42
8.Электрон, прошедший ускоряющую разность потенциалов 500 В, попал в вакууме в однородное магнитное поле и движется по окружности радиусом 10 см. Определите модуль магнитной индукции, если скорость электрона перпендикулярна силовым линиям.
Дано:
U=500B R=0,1м
B
B ?
Решение. На электрон действует сила Лоренца, которая по правилу левой руки направлена к центру окружности и является центростремительной.
Сила Лоренца равна: Fл evB . Тогда mvR2 evB B mveR ,
где e 1,6 10 19 Кл – заряд электрона; m 9,1 10 31кг– масса электрона.
|
|
|
|
|
|
|
|
|
|
|
mv2 |
2eU |
|
По закону сохранения энергии: |
eU |
|
v |
m . |
|||||||||
2 |
|||||||||||||
|
|
|
m |
|
2eU |
|
1 |
2mU . |
|
|
|
||
Значит, |
B |
|
|
|
|
m |
|
|
|
|
|||
|
|
|
eR |
|
|
|
|
||||||
|
|
|
|
|
|
R |
e |
|
|
|
|||
Получаем, B |
1 |
|
|
2 9,1 10 31 |
500 |
7,54 10 4 |
Тл . |
||||||
0,1 |
|
1,6 10 19 |
|||||||||||
|
|
|
|
|
|
|
|||||||
Ответ: B 7,54 10 4Тл.
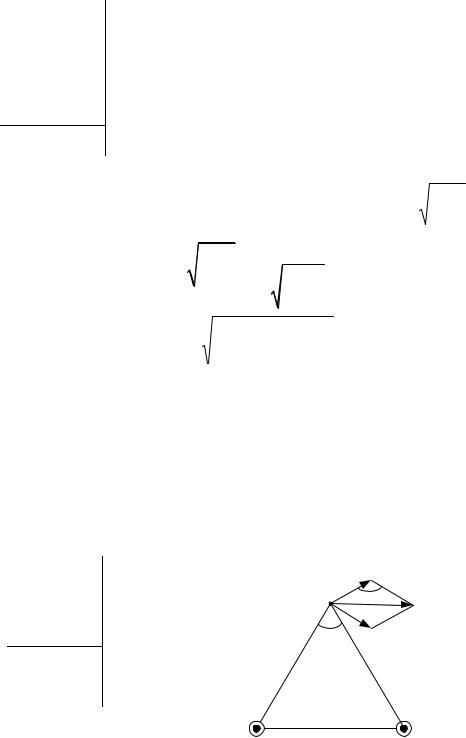
9.По двум длинным параллельным проводам, расстояние между которыми 5 см, в одинаковом направлении текут одинаковые токи 10А. Определить индукцию и напряженность магнитного поля в точке, удаленной от каждого провода на расстояние 5 см.
Дано: B2
d=0,05м |
Решение. |
|
|
I=10A |
B |
||
|
|||
|
B1 |
||
B-? |
|||
d |
d |
||
H-? |
|||
|
|
||
|
I |
I |
|
|
d |
|
Рис.3
43
Из рис. 3 видно, что 60 (равносторонний треугольник), значит, 120 . Магнитная индукция от прямого проводника равна:
B1 B2 0I ,
2 d
где o 4 10 7 Гнм – магнитная постоянная.
|
По теореме косинусов: B |
B2 B2 |
2B B cos . |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
1 |
2 |
|
|
|
|
|
|
|
Так как B B |
и cos cos120 0,5, то B B2 |
B2 |
B2 |
B 3 . |
||||||||||||||||
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
|
1 |
|
|
Значит, B |
3 0I |
. |
Напряженность магнитного поля равна: |
H |
B |
. Значит, |
||||||||||||||
|
|
|
|
2 d |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||||
H |
3I |
. |
Получаем, |
|
B |
|
3 4 10 7 |
10 |
6,93 10 5Тл, |
|
|
|
|
|
|
||||||
|
|
|
2 0,05 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
H |
3 10 |
|
55,16 |
А |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 3,14 0,05 |
м . |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Ответ: В=6,93ּ10-5Тл, |
|
Н=55,16 А/м. |
|
|
|
|
|
|
|
|
||||||||||
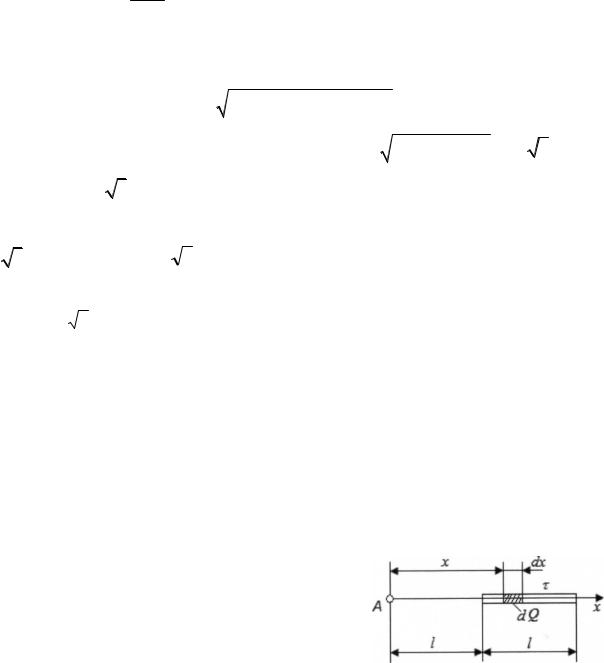
10. На тонком стержне длиной l равномерно распределен заряд с линейной плотностью τ = 10 нКл/м. Найти потенциал φ, созданный распределенным зарядом в точке А, расположенной на оси стержня и удаленной от его ближайшего конца на расстояние l.
Решение. В задаче рассматривается поле, создаваемое распределенным зарядом. В этом случае поступают следующим образом. На стержне выделяют малый участок длиной dx. Тогда на этом участке
будет сосредоточен заряд dQ = τ dx, который можно Рис. 4 считать точечным. Потенциал dφ, создаваемый этим
точечным зарядом в точке А (рис. 4), можно определить по формуле
d |
dQ |
|
dx |
|
|
|
. |
||
4 o x |
4 o x |
|||
44
Согласно принципу суперпозиции электрических полей, потенциал электрического поля, создаваемого заряженным стержнем в точке А, найдем интегрирование этого выражения:
2l |
dx |
|
|
2l dx |
l |
|
|
|
l x . |
4 o x |
4 o |
Выполним интегрирование:
4 o ln 2 .
Подставим числовые значения физических величин в СИ (τ=10ּ10-9 Кл/м, 1/(4πεo) = 9·109 м/Ф) и произведем вычисления:
φ = 9·109·10·10-9·0,693 = 62,4 В. Ответ: φ = 62,4 В.
11.На пластинах плоского конденсатора находится заряд Q = 10 нКл. Площадь S каждой пластины конденсатора равна 100 см2, диэлектрик – воздух. Определить силу F, с которой притягиваются пластины. Поле между пластинами считать однородным.
Решение. Заряд Q одной пластины находится в |
|
|
поле напряженностью E, созданной зарядом другой |
|
|
пластины конденсатора. Следовательно, на первый за- |
|
|
ряд действует сила (рис. 5) |
|
|
F = QE. |
(1) |
Рис. 5 |
Так как
Е = σ/(2ε0) = Q/(2ε0S),
где σ – поверхностная плотность заряда пластины, то формула (1) примет вид
F = Q2/(2ε0S).
Произведем вычисления:
F |
|
10 16 |
|
5,65 10 4 |
Н 565мкН . |
|
2 |
8,85 10 12 |
10 2 |
||||
|
|
|
Ответ: F=5,65ּ10-4Н.
45