1.Предмет теории вероятности. Виды событий. Действия над событиями.

Любая точная наука изучает не сами явления и процессы, а их математические модели.

Существуют задачи, когда совокупное влияние случайных факторов придающих конкретному опыту существенное влияние превышают или сравнимы с действиями основных факторов, выявленные в задачах с закономерностями, называют вероятностными или статистическими.

Теория вероятности – математическая наука, изучающая закономерности массовых случайных явлений.

Предметом теории вероятности является математические модели случайных явлений.

Под случайным явлением понимается явление, исход которого заранее предсказать нельзя.

Цель теории вероятности – осуществление прогноза в области случайных явлений, их контроль и т.п.

Результаты любого опыта можно характеризовать качественно и количественно.

Качественной характеристикой результата является событие.

События принято делить на достоверные, невозможные и случайные.

Достоверное - событие, которое обязательно произойдет при выполнении определенного комплекса условий.

Пример: «Тяжелый шарик на наклонной плоскости покатится обязательно в сторону»

Невозможное – событие, которое обязательно не произойдет при выполнении определенного комплекса условий.

Пример: «Из герметично закрытого сосуда вода не может вылиться».

Случайное – событие, которое при определенном комплексе условий, либо произойдет, либо не произойдет.

Пример: «Уроненная на пол чашка, либо разобьется, либо останется на поврежденной»

События называются несовместными, если появление в 1-ом и тот же испытании 1-ого из них полностью исключает появление других событий.

Пример: «Попадание и промах при выстреле по цели»

В противном случае – события называются совместными.

Несколько событий образуют полную группу, если появление 1-ого из них является достоверным событием.

Несколько событий называют равновозможными, если при проведении опыта могут произойти несколько событий и каждое из них не является более возможным, чем другое.

Основные операции проводятся аналогично основным операциям над множествами.

Сумма А и В называется событие С=А+В, состоящее в появлении событий А и В вместе.

Произведение А и В называется событие С=А*В, состоящее в появлении событий А и В одновременно.

Противоположное событие А происходит тогда и только тогда, когда событие А не происходит.

Разностью событий А и В называется событие С=А-В, означающее, что событие А-происходит, В – не происходит.

Множество всех элементарных событий обозначается омегой.

Достаточное событие-

Невозможное-.

2. Свойство статистической устойчивости относительной частоты событий. Статистическое определение вероятности.

Пусть в «n» повторяющихся опытах некоторое событие А наступилоn_А раз.

Число n_A называетсячастотой события А в рассматриваемой серии опытов.

Отношение n_A/n=P*(A) называетсяотносительной частотой(частотностью)события А.

(1.1)

Относительная частота события обладает следующими свойствами:

1. Частота любого события заключается между 0 и 1.

2. Частота невозможного события равна 0.

3. Частота достоверного события равна 1.

4. Частота суммы двух несовместных событий равна сумме частот этих событий.

Частота обладает еще одним свойством – свойством статистической устойчивости– с увеличением числа опытовn, она принимает значения близкие к некоторому постоянному числу. В этом случае говорят, что частота стабилизируется, приближаясь к некоторому числу.

Пример.

В опыте бросания монеты относительная частота появления герба при 4040 бросаний оказалась равна 0,5096 = 2048/4040. При 12000 и 24000 она оказалась соответственно равна 6018/12000 = 0,5015 и 12012/24000 = 0,5005. Таки образом частота приближается к числу 0,5.

Отметим, что теория вероятности изучает только те массовые случайные явления с неопределенным исходом, для которых предполагается наличие устойчивой относительной частоты.

Количественной характеристикой события является Вероятность события, т.е. число, выражающее степень возможности его появления в данном опыте. Существует несколько математических определений вероятности, дополняющих и обобщающих друг друга.

Рассмотрим определение, в основе которого лежит выражение (1.1)

Статистическая вероятность– число, около которого колеблется относительная частота события А при достаточно большом числе опытов.

(1.2)

Вероятности Р(А) приписывают свойства 1-4 относительной частоты.

Классическое определение вероятности. Свойство вероятностей. Элементы комбинаторики.

Пусть проводится опыт с n исходами, которые можно представить в виде полной группы несовместных равновозможных событий, называемых элементарным событием.

Элементарное событие, приводящее к появлению событию A, называется благоприятным, или благоприятсвующими событию А.

Вероятность события A называется отношение m – элементарное событие, благоприятсвующее к событию А, к общему числу n – равновозможные несовместных элементов событий, образу.щих полную группу.

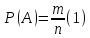
Из данного определения выполняются свойства вероятности (P):

1. 

2. вероятность достоверного события

3. вероятность невозможного события

4. вероятность случайного события

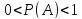5. Вероятность суммы несовместных событий

6. Вероятность суммы противоположных событий = 1

Расчет вероятностей обычно производится по формулам комбинаторики.

Комбинаторика – это раздел математики, в котором изучаются задачи выбора элемента из заданного множества и расположения их в группы по определенным правилам.

Многие комбинаторные задачи решаются с помощью двух правил: умножения и сложения.

Правило умножения: Если из некоторого известного количества конечного множества первый объект (элемент Х) можно выбрать n1 способами и после каждого (элемента Y) n2 способами, то оба объекта X и Y можно выбрать в указанном порядке n1*n2 способами.

Пример 1: Сколько 3-х значных чисел можно составить из цифр 1,2,3,4,5, если:

1. цифры не повторяются

2. Цифры могут повторяться

1. Для выбора 1 цифра имеется 5 вариантов (n1=5), для выбора 2-ой цифры - 4 варианта (n2=4), для выбора 3-ой цифры (n3=3)

2. Для выбора 1-ой цифры (n1=5), для выбора 2-ой цифры (n2=5), для выбора 3-ой цифры (n3=5)

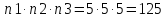
Правило суммы:

Если некоторый объект Х можно выбрать n1 способами, а второй объект Y n2 способами, при чем 1-ый и 2-ый способны пересекаться, то любой из указанных объектов логично выбрать n1+n2 способами.

Пример 2: В студенческой группе 15 девушек и 10 юношей, сколькими способами можно выбрать двух студентов одного пола.

По правилу умножения двух девушек можно выбрать: девушек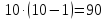юношей

Существуют две схемы выбора m элементов из исходного множества:

1. без возвращения (без повторений)

2. с возвращениями (с повторения)

Схемы выбора без возвращения. Схемы выбора с возвращением.

Рассмотрим схемы без возвращения. Пусть дано множество из n различных компонентов. Перестановками из n различных элементов и отличающимися полным порядком расположения

Размещение из n элементов по m элементам называется комбинацией по m элементам и отличающиеся друг от друга либо порядком расположения элемента, либо элементами.

Пример 3: Сколько комбинаций, отличающихся элементами и их расположением, из 10 цифр по 3.

Сочетаниями из n элементов по m элементам называется комбинации по m элементам и отличающихся друг от друга хотя бы одним знаком.

Пример 4: Сколько комбинаций можно составить из 10 частей по 3 отличающихся хотя бы одним числом.

Схема выбора с возвратом.

Пусть в множестве с n элементами есть k различных элементов, при чем 1-ый элемент повторяется n1 раз, 2-ой – n2 … k-ый – nk раз, причем n=n1+n2+…+nk.

Перестановками из n элементов данного множества называют перестановками с повторениями (с возвращениями) из n элементов, число которых вычисляется по формуле:

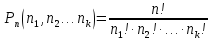
Пример 5: Сколько различных 5-значныз чисел можно составить из: 3,3,7,7,9

Если при выборе m элементов из n элементов возвращаются обратно и упорядываются, то говорят, что это размещение с повторением.

Размещение с повторением могут отличаться друг от друга элементами, их порядком и количеством. Число таких размещений.

Пример 6: Сколько 5-значных чисел можно составить из цифр 2,3,7,9:

Если при выборке m элементов из n элементов возвращаются, но не упорядываются, то говорят, что это сочетание с повторением:

Пример 7: Сколькими способами можно составить букет из 5 цветов, если в наличие есть цветы трех сортов.

m=5, n=3

Условия вероятности. Вероятность произведения событий.

Пусть А и В-события, рассматриваемые в данном опыте. Наступление одного из этих событий (А) может повлиять на появление одного из другого события (В). Для характеристики зависимости одного события из другого вводят понятие условной вероятности.

Условной вероятностью события (В) при условии, что событие (А)ужепроизошло называется отношение вероятности произведения событий А и В к вероятности события (А):

Р(В/А) = Р(АВ)/Р(А) (1)

Вероятность Р(А)в отличии от условной вероятности наз.безусловной вероятностью.

Аналогично, вероятность события (А) при условии, что событие (В) уже произошло определяют формулой:

Р(А/В) = Р(АВ)/Р(В) (2)

ПРИМЕР: В урне3белых и7черных шаров. Из них вытаскивают2шара. Какова вероятность того, что 2ой шар будет белый, при условии, что 1ый есть черный.

ПУСТЬ:А - 1ый шар черный;

В – 2ой шар белый

Р(А) = 7/10

Р(В)_А = 3/9 = 1/3.

Р(АВ) = Р(А/Р(В/А)) = Р(В)*Р(А/В) (3)

Вероятность произведений 2х событий равна произведению безусловной вероятности одного из событий на условную вероятность 2ого события, при условии, что 1ое произошло.

Выражение (3) наз. правилом условной вероятности. Для случая большого числа соб. А₁, А₂, ... , А_n. Это правило записывают в видеР(А₁, А₂, … , А_n) = Р(А₁)*Р(А₂/А₁)*Р(А₃/А₁А₂)* … *Р(А_n/А₁А₂А_n-1).

Правило условности имеет более простой вид, если рассматривать события независимыми, т. е. условная вероятность события равна его безусловной вероятности.

Р(А/В) = Р(А)

Р(АВ) = Р(А)*Р(В) или для случая nнезависимых событий имеет вид:

Р(А₁*А₂* … *А_n) = Р(А₁)*Р(А₂)* … *Р(А_n)

Из свойств вероятности известно, что вероятность суммы 2х несовместных событий равна сумме их вероятностей:

Р(А+В) = Р(А) + Р(В)

Вероятность суммы 2х совм. событий опр. выражение:

Р(А+В) = Р(А) + Р(В) – Р(АВ)

А В

АВ

Для 3х событий А, В, С: Р(А+В+С) = Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) + Р(АВС)

В

АВС

С

А

Формула полной вероятности.

Одним из следствий совместного применения теорем сложения и умножения вероятностей являются формулы полной вероятности и Байеса.

События А₁,А₂…,А_n образуют полную группу, если А_i*Аj≠ɸ, i≠j и . Систему таких событий называют разбиением

Теорема:

Пусть события Н₁,Н₂,…Н_n образуют полную группу. Тогда для любого, наблюдаемого в опыте события А имеет место формула полной вероятности.

P(A)=∑P(A∣Нi)*P(Нi).

Т.к. Н₁+Н₂+…+Н_n=Ω, то в силу свойств операций над событиями А=А*Ω=А*(Н₁+Н₂+…+Н_n)=А* Н₁+А* Н₂+…+ А* Н_n. Из того, что Н_i*Н_j=ɸ следует, что (А*Н_i)*(А* Н_j)= ɸ, i≠j, т.е. события А*Н_i и А* Н_j также несовместны. Тогда по теореме сложения вероятностей Р(А* Н₁)+Р(А* Н₂)+…+Р(А* Н_n) т.е. Р(А)=. По теореме умножения вероятностей Р(А*Н_i)= P(A∣Н_i)*P(Н_i).

События Н₁,Н₂…Н_n обычно называют гипотезами, они исчерпывают все возможные предположения(гипотезы) относительно исходов как бы первого этапа опыта, события А-один из возможных исходов второго этапа. ЖОПА.

Пример: В сборочный цех поступает 40% деталей из цеха 1 и 60% из 2 цеха. В 1 цехе производится 90% стандартных деталей, а во 2-95%. Найти вероятность того, что взятая на удачу сборщиком деталь окажется стандартной.

Решение: Взятие детали можно разбить на два этапа. Первый- выбор цеха. Имеется две гипотезы:Н₁-деталь изготовлена цехом 1, Н₂-2 цехом. Второй этап взятие детали. Событие А-взятая наудачу деталь стандартна. Очевидно, события Н₁,Н₂ образуют полную группу, Р(Н1)=0,4, Р(Н2)=0,6. Числа 0,90 и 0,95 являются условными вероятностями события А при условии гипотез Н1 и Н2 соответственно, т.е. Р(А|Н₁)=0,90 и Р(А|Н₂)=0,95. По формуле полной вероятности находим Р(А)=

Формула Байеса.

Следствием формулы полной вероятности является формула Байеса или теорема гипотез. Она позволяет переоценить вероятности гипотез Н_i, принятых до опыта и называемых априорными по результатам уже проведенного опыта, т.е. найти условные вероятности Р(Н_i|A), которые называют ЖОПА апостериорными (после опыта)

Теорема: Пусть события Н₁,Н₂,…Н_n образуют полную группу. Тогда условная вероятность события Н_k(k=1,n) при условии, что событие А произошло, задается формулой

P(H_k|A) = P(A|H_k) · P(H_k) / P(A)

Где Р(А)=Р(Н₁)*Р(А|Н₁)+…Р(Н_n)*P(A|H_n)-формула полной вероятности.

Пример:

Определим вероятность гипотезы Н₂ при условии, что событие А (взятая деталь стандартна) уже произошло, т.е. Р(Н₂|А):

Р(Н₂|А)= P(H_k|A) = P(A|H_k)* P(H_k) / P(A)= 0,6*0,95/0,93=0,613

6-ой параграф.