
2. Расчёт механической энергии в машине атвуда
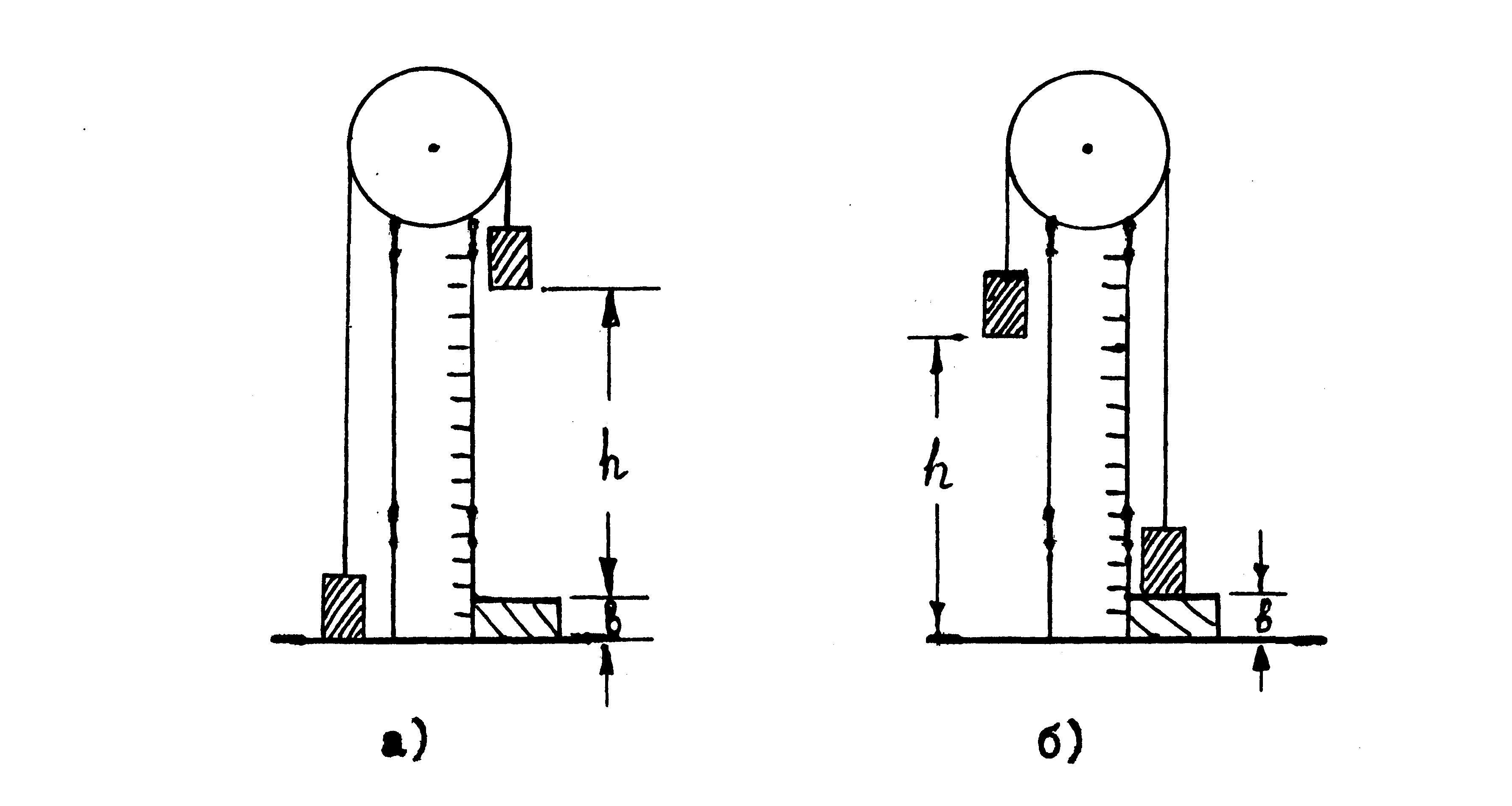
Рис. 1П
Принимаем начальный уровень потенциальной энергии левого груза П02=0 (рис. 1П-а). Тогда П01= m1 g (h + b) , где b - высота подставки, на которую опускается правый груз с массой m1 .
Учтём, когда левый груз находится внизу - система ещё покоится значит кинетическая энергия Т0 = 0.
После начала движения грузов у системы появляется кинетическая энергия:
 ,
(3П)
,
(3П)
где
 - линейные скорости грузов,
- линейные скорости грузов,
 -
угловая скорость блока,
-
угловая скорость блока,
J - момент инерции блока.
Скорости
 и
и здесь связаны простым соотношением:
здесь связаны простым соотношением:
 бл
,
(4П)
бл
,
(4П)
т. к. скорости грузов равны скорости точки схода нити с поверхности блока.
С учётом (4П) запишем формулу (ЗП) для конечного момента времени:
 ,
(5П)
,
(5П)
где
 - скорость груза в момент опускания на
подставку.
- скорость груза в момент опускания на
подставку.
Подставляя в (2П) выражения для начальной и конечной энергии, получим:
 ,
(6П)
,
(6П)
или:
 (7П)
(7П)
Расчётное задание
Скорости
грузов для каждого конечного момента
времени (т.е. времени спуска
 )
определяются простым выражением:
)
определяются простым выражением:
 ,
(8П)
,
(8П)
т. к. ускорения при движении постоянные и начальные скорости равны нулю.
Необходимо
с учётом найденного в опыте момента
инерции блока 3 выполнить расчёты
механической энергии для пяти случаев
опускания грузов с массами
 ÷
÷ .
.
Для этого вычислить разность потенциальной энергии в начальном и конечном положениях грузов:

и кинетическую энергию системы для конечного момента времени:

Определить коэффициент полезного действия (кпд):
 (9П)
(9П)
Данные расчёта привести в таблице:
Таблица
|
|
Энергия (П0-Пк), Дж |
Энергия Тк , Дж |
Разность энергий (П0 - Пк) – Тк, Дж |
КПД |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ВНИМАНИЕ: все расчёты выполнять с точностью до четвёртого знака после запятой в десятичных дробях, использовать значение g = 9,8149 м/с2.
Потери энергии (т.е. разность потенциальной и кинетической энергии) сравнить с работой момента сил трения Мтр , найденного из опыта. Работа момента сил трения определяется формулой:
 ,
(10П)
,
(10П)
где
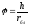 - угол поворота блока за время опускания
груза с высотыh.
- угол поворота блока за время опускания
груза с высотыh.

 Масса
Масса
 ,
кг
,
кг