6. Литература
6.1. Савельев И.В. Курс общей физики, т.1, Москва, «Наука», 1977г.
6.2. Трофимова Т.И. Курс физики, Москва, «Высшая школа», 2003г.
6.3. Терентьев А.Д. Введение в физику: основы физических измерений, Методическое пособие № 100, КГТУ, 2006г.
ПРИЛОЖЕНИЕ 1
ИССЛЕДОВАНИЕ НЕКОТОРЫХ СВОЙСТВ ДВИЖЕНИЯ НА УСТАНОВКЕ МАКСВЕЛЛА И ОПРЕДЕЛЕНИЕ СРЕДНЕЙ И МАКСИМАЛЬНОЙ СИЛ НАТЯЖЕНИЯ ПРИ РЫВКЕ НИТИ
Примечание. В приложении 1 рассматривается скатывание тел на "идеализированных", т.е. абсолютно упругих, нерастяжимых, гладких нитях при отсутствии потерь механической энергии. Получен ряд формул, характеризующих свойства механического движения при скатывании тел по отвесным нитям. Дано сравнение сил натяжения, действующих на тело во время скатывания по нити и во время рывка в нижней точке спуска..
1. На рис. 1-П1 дана схема, на которой показан цилиндр радиуса r в процессе скатывания, т. е. движения "вниз". Принимаем, что скатывание происходит по двум нитям. Цилиндр может являться осью, на которой закреплено другое симметричное тело, например, шар или диск радиуса
R > r (на схеме не показано), тогда r - это радиус намотки нити. Сила натяжения обозначена S0 и равна удвоенной силе натяжения каждой нити. Сила тяжести G приложена в центре масс. В т. P в каждый момент времени расположен мгновенный центр скоростей (м. ц. с.) и через него проходит мгновенная ось вращения. Считаем, что за время tk нити полностью разматываются, и центр масс опускается с высоты h.
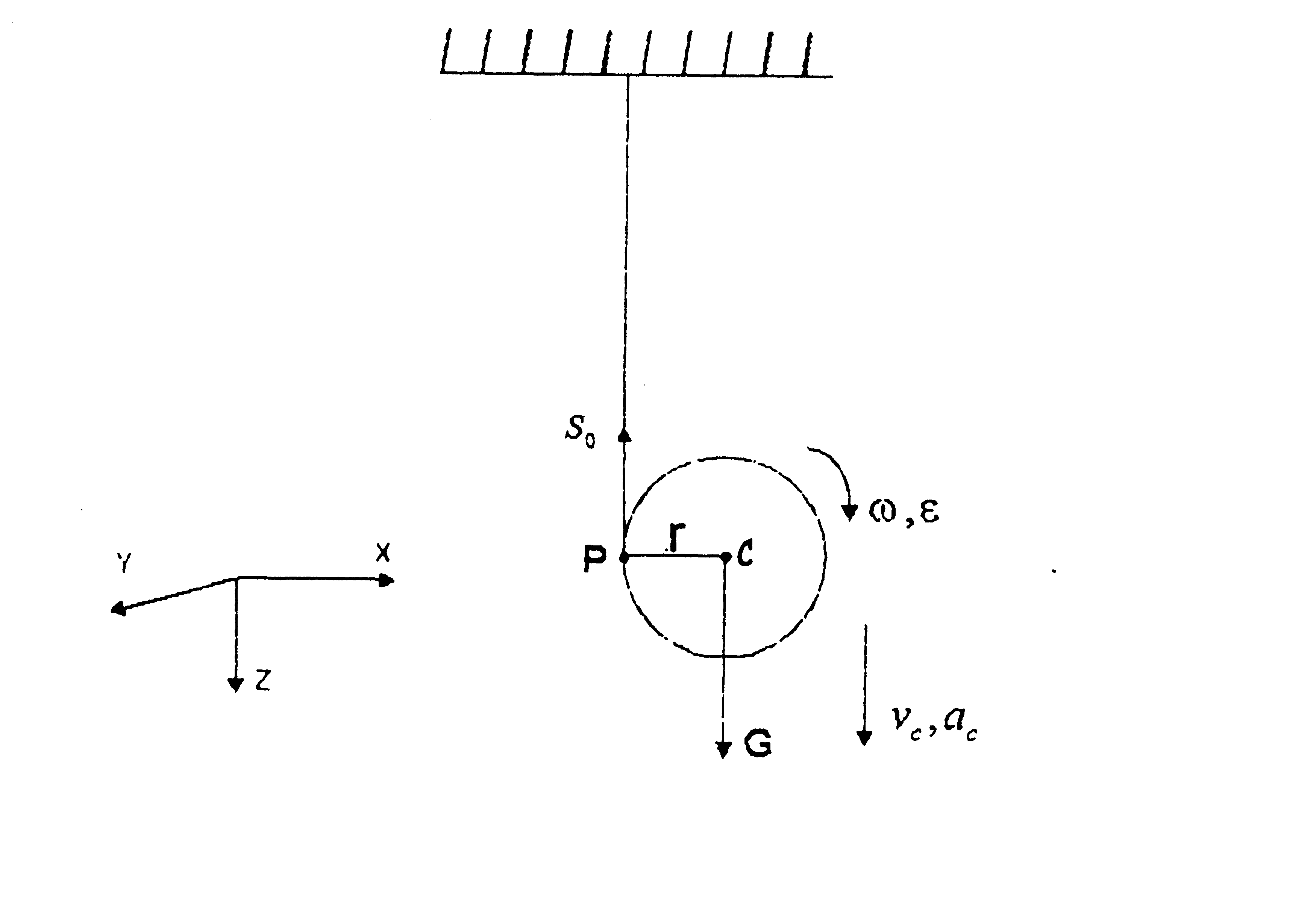
Рис. 1-П1
Для расчёта силы
S0
и скорости
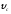 в конце спуска используем уравнения
динамики вращательного движения тела
относительно осей в точкахС
и Р,
дополненные условием кинематической
связи между ускорениями
в конце спуска используем уравнения
динамики вращательного движения тела
относительно осей в точкахС
и Р,
дополненные условием кинематической
связи между ускорениями
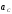 и
и и формулами для пути
и формулами для пути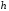 и скорости
и скорости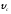 центра масс при равнопеременном,
прямолинейном движении из начального
состояния покоя:
центра масс при равнопеременном,
прямолинейном движении из начального
состояния покоя:
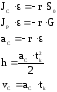 (1П-1)
(1П-1)
В уравнениях
(1П-1) полагаем известными значения:
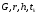 ,
,
где
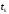 -время спуска с высоты
-время спуска с высоты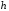 .
.
После почленного деления первого уравнения на второе,
получаем для величины (модуля) силы натяжения следующую
формулу:
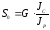 (1П-2)
(1П-2)
где
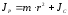 ;
;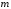 - масса;
- масса; - радиус намотки нити.
- радиус намотки нити.
Значение
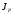 определяем из второго уравнения с
помощью
определяем из второго уравнения с
помощью
третьего и четвертого уравнений.
Величину (модуль) скорости центра масс при спуске с высоты
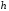 можно найти с
помощью формул, которые получаются из
системы
можно найти с
помощью формул, которые получаются из
системы
(1П-1):
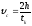
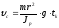
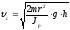 (1П-3)
(1П-3)
Общий вид выражения для ускорения центра масс тела при
скатывании определяется дифференцированием по времени второй
формулы скорости в (1П-3). В результате получаем:
 (1П-3а)
(1П-3а)
Ускорение
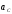 оказывается постоянным и не зависящим
от массы
оказывается постоянным и не зависящим
от массы
тел,
т.к. момент инерции
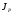 включает в себя массу в качестве сомно-
включает в себя массу в качестве сомно-
жителя.
Формулы для скорости
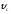 эквивалентны между собой
эквивалентны между собой
и могут применяться в зависимости от условий и цели исследования.
Например, рассмотрим, как вторая формула в (1П-3) позволяет найти
общую формулировку закона движения центра масс тела
вдоль вертикальной оси Z.
Для
этого надо учесть, что скорость![]() ,задать начальные
,задать начальные
условиядля
координаты и скорости центра масс и
выполнить интегрирование.
Помещая начало координат в точку подвеса
нити и принимая,
что при t0
=0
начальная координата т. С
равна
Zo
и
начальная скорость
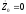 ,
запишем (для произвольного времениt):
,
запишем (для произвольного времениt):
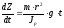 (1П-4)
(1П-4)
Разделяя в (1П-4) переменные (умножая обе части на дифференциал
dt)
и
учитывая, что величина
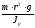 -
постоянная,
получим
-
постоянная,
получим
после интегрирования:
 (1П-5)
(1П-5)
где С - константа, определяемая из начальных условий. При подстановке
в (1П-5) начальных данных (при to = 0) получаем: C = Zo.
Окончательная формулировка для закона движения центра масс тела
при
скатывании
по отвесной нити из состояния покоя
(т. е.
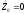 )
)
с учётом (1П-3а) имеет вид:
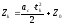 (1П-6)
(1П-6)
Из формулы (1П-6) определяется высота спуска h как разность координат
центра масс в конечный момент времени tk и начальный момент времени t0:
 (1П-7)
(1П-7)
Отметим характерную особенность при скатывании по
нитям в гравитационном поле, состоящую в том, что все кинемати-
ческие параметры,
т. е. линейные и угловые скорости и ускорения, не зависят от
массы скатывающихся тел. Однако имеется сильная зависимость от
радиуса намотки нити и пространственной конфигурации тела, определяю-
щей его момент инерции.
2. На рис. 2-П1 дана схема разворота тела в конце спуска после
полной размотки нити. В этом положении качение по нити прекратилось
и т. Р - это точка закрепления нити на поверхности, через которую проходит
ось вращения тела. По отношению к нити - в начале и в конце разворота –
тело всегда будет иметь положение, показанное на рис. 2-П1. При разворо-
те одновременно происходит переброска нити, так что в конце разворота
т. Р оказывается на другой стороне от т. С по сравнению с её положением
в начальный момент времени.
Для лучшего понимания процесса разворота рассмотрим неподвижную ось,
на
которой закреплён конец стержня (см.
рис. 3-П1). Если стержень вначале
установить в горизонтальном положении
справа и затем отпустить,
то, совершив поворот вокруг оси на угол
 ,
он окажется
в горизонтальном
положении слева. Такое же перемещение
произойдёт с телом
любой формы, в том числе с диском, если
ось поворота не совпадает с центром
масс тела.
,
он окажется
в горизонтальном
положении слева. Такое же перемещение
произойдёт с телом
любой формы, в том числе с диском, если
ось поворота не совпадает с центром
масс тела.
Примечание. Устройство, включающее в себя твёрдое тело, подвешенное в гравитационном поле на оси, не проходящей через центр масс, называется физическим маятником. В таком маятнике, если он не находится в состоянии равновесия, происходят колебания, которые могут быть линейными либо нелинейными. Рассматриваемый здесь процесс разворота тела на оси представляет собой цикл нелинейных колебаний. Следовательно, все явления в нижней точке спуска тела (после скатывания по нити) можно было бы изучать методом теории нелинейных колебаний.
Однако особенность процесса в нижней точке спуска на нити в том, что колебания завершаются на одном полупериоде (т. к. после разворота вращающееся тело начинает катиться по нити "вверх", наматывая нить на свою поверхность). Математическое описание физики явлений на этом интервале времени можно выполнить без привлечения специальных методов теории колебаний.
Вернёмся
к схеме рис. 2-П1. Здесь показано, что в
начальный момент времени разворота
скорость центра масс и угловая скорость
тела имеют значения
v0
и ω0.
Очевидно, эти значения равны
скоростям, приобретённым
телом в конце спуска с заданной высоты
h.
Пунктиром
на схеме
изображена траектория центра масс -
это дуга окружности радиусом r
и
длиной
 r
. В
процессе разворота скорости
r
. В
процессе разворота скорости
 иω
вначале растут и достигают
максимальных значений в нижнем положении
тела.
иω
вначале растут и достигают
максимальных значений в нижнем положении
тела.
В
конце разворота скорости
 иω
должны иметь такие же значения, как и
в начальный момент времени, т. к. принято
условие абсолютной упругости
и нерастяжимости нити. При развороте
тела работу выполняет только потенциаль-
иω
должны иметь такие же значения, как и
в начальный момент времени, т. к. принято
условие абсолютной упругости
и нерастяжимости нити. При развороте
тела работу выполняет только потенциаль-
ная сила тяжести. Сумма таких работ при опускании и подъёме центра масс
на одну и ту же высоту h равна нулю, что и доказывает равенство скоростей в нача-
ле и конце разворота
В ходе разворота тела вокруг оси в т. Р происходит кратковремен-
ное увеличение силы натяжения нити, называемое рывком нити. Вре-
мя
разворота
равно времени рывка. Этот интервал
времени
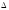 t
мож-
t
мож-
но приближённо оценить, считая, что центр масс движется по дуге длиной
 r
с
постоянной скоростью,
r
с
постоянной скоростью,
равной
начальной скорости
 :
:
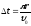 (1П-8)
(1П-8)
Используя только теорему импульсов для точки, можно также приближённо оце-
нить среднюю силу натяжения Sср за время рывка Δt. Согласно этой теоре-
ме: импульс сил
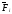 ,
приложенных к материальной точке, равенизмене-
,
приложенных к материальной точке, равенизмене-
нию (приращению) импульса самой точки:
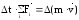 (1П-9)
(1П-9)
Принимая за материальную точку центр масс тела, к которому приложены
две противоположно направленные силы scp и G, затем учитывая, что в
проекции
на вертикаль имеем: Δ
(т·
 )
= -2 ·т·
)
= -2 ·т·
 , получим:
, получим:
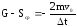 (1П-10)
(1П-10)
В формуле (1П-10) учтено, что ось Z направлена вниз, scp- это некоторая
усреднённая за время разворота проекция силы натяжения нити на ось Z, G –
сила тяжести.
Подставляя в (1П-10) значение Δt из (1П-8), имеем:
 (1П-11)
(1П-11)
Формула (1П-11) даёт несколько заниженную величину силы scp, т. к.
не учитывает ускоренное движение центра масс за время разворота тела.
Кроме того, рассмотренный приближённый метод расчёта не позволяет
найти максимальное значение силы натяжения в ходе переброски нити.
Для более точных вычислений применим уравнение динамики
вращательного движения тела вокруг оси в т. Р. Решение такого уравне-
ния позволяет найти скорость центра масс как функцию угла поворота и затем
рассчитать центростремительную силу, приложенную в т. С.
На рис. 4-П1 изображено тело в процессе разворота. Углы поворота тела φ
либо
α
связаны простымсоотношением:![]() .Мгновенные (т. е.
для дан-
.Мгновенные (т. е.
для дан-
ного
момента времени и угла поворота) значения
скоростей и сил обозначены "звездочкой".
Показано, что центростремительная сила
![]() равна и противоположна силеF*,
приложенной к т. Р
и увеличивающей натяжение
равна и противоположна силеF*,
приложенной к т. Р
и увеличивающей натяжение
нити S*, т. к. проекция Fя* суммируется с силой G.
Используя условие равновесия (покоя) для т. Р, запишем сумму проек-
ций мгновенных сил на ось Z:
G+FZ*-S*=0 (1П-12)
где FZ* =F*∙ sin a .
Применим уравнение динамики вращательного движения
для определения угловой скорости тела и затем скорости центра масс:
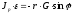 (1П-13)
(1П-13)
Умножая
в (1П-13) обе части равенства на
![]() и учитывая
и учитывая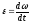 и
и ,
получим:
,
получим:
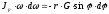 (1П-14)
(1П-14)
Интегрирование (1П-14) дает:
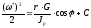 (1П-15)
(1П-15)
где
С
- константа, определяемая начальными
условиями: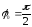 и
и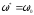
т.е.
С =
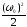 .
.
Заменяя
в (1П-15) угол
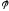 на угол
на угол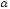 с учётом
с учётом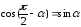 и
и
используя формулу Эйлера для скоростей точек вращающегося тела, получим:
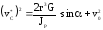 (1П-16)
(1П-16)
Далее, применяя формулу для центростремительной силы
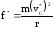 (1П-17)
(1П-17)
и
учитывая, что
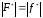 ,
получаем для проекции на ось Z мгновенного
значения силы
,
получаем для проекции на ось Z мгновенного
значения силы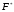 выражение:
выражение:
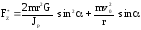 ,
(1П-18)
,
(1П-18)
где
угол
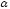 изменяется от 0 (в начале разворота) до
изменяется от 0 (в начале разворота) до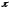 (в конце разворота) Мгновенное значение
силы натяжения нити, согласно (1П-12),
равно
(в конце разворота) Мгновенное значение
силы натяжения нити, согласно (1П-12),
равно
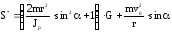 (1П-19)
(1П-19)
Из
(1П-19) следует, что максимальное значение
силы натяжения нити достигается при
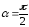 ,
т. е. в нижнем положении тела (см. рис.
2-П1). Максимальная мгновенная сила
равна:
,
т. е. в нижнем положении тела (см. рис.
2-П1). Максимальная мгновенная сила
равна:
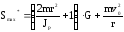 (1П-20)
(1П-20)
Для определения среднего значения силы натяжения за время рывка,
т. е. за время полного разворота тела, необходимо выполнить усреднение
по
углу поворота, равному
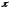 .
Процедура усреднения состоит в том,
«что вначале задаётся элементарное
значение силы
.
Процедура усреднения состоит в том,
«что вначале задаётся элементарное
значение силы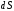 на элементарном угле поворота так, что
на элементарном угле поворота так, что ,
затем - все значения
,
затем - все значения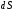 суммируются, т е. вычисляется интеграл
на промежутке углов
суммируются, т е. вычисляется интеграл
на промежутке углов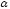 от 0 до
от 0 до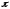 ,
и окончательное решение, т. е. среднее
значение силы, получается делением
результата суммирования (интегрирования)
на полный интервал углов, равный
,
и окончательное решение, т. е. среднее
значение силы, получается делением
результата суммирования (интегрирования)
на полный интервал углов, равный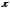 .
.
Запишем:
 (1П-21)
(1П-21)
Обозначая
среднее значение силы натяжения -
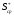 ,
получаем выражение
,
получаем выражение
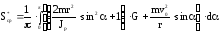 (1П-22)
(1П-22)
Несложное интегрирование в (1П-22) приводит к результату:
 (1П-23)
(1П-23)
Формула
(1П-23) показывает, что точное значение
средней силы натяжения
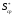 за время рывка нити больше значения
за время рывка нити больше значения ,
вычисляе-
,
вычисляе-
мого в (1П-11), на величину, равную:
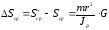 (1П-24)
(1П-24)
Например, для однородного цилиндра с радиусом, равным радиусу
намотки
нити, разница сил натяжения
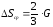 .
С уменьшением радиуса намотки нити и
с увеличением момента инерции
.
С уменьшением радиуса намотки нити и
с увеличением момента инерции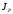 эта
эта
разница уменьшается.
Сравнение формул (1П-20) и (1П-23) показывает, что максимальное значение мгновенной силы натяжения заметно превышает среднее
значение той же силы за время рывка нити. Разность этих сил равна:
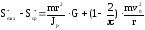 (1П-25)
(1П-25)
Для сравнения средней силы натяжения при рывке нити с силой натяжения
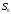 во время скатывания
тела преобразуем формулу (1П-23) к другому
виду. Учитывая:
во время скатывания
тела преобразуем формулу (1П-23) к другому
виду. Учитывая:
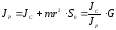 (см. формулу (1П-2)),
(см. формулу (1П-2)),
из (Ш-23) получим:
 (1П-26)
(1П-26)
Простые
расчёты показывают, что в зависимости
от высоты спуска и конфигурации
скатывающегося тела, значение
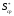 может многократно превосходить значение
может многократно превосходить значение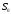 .
.
В
ряде исследований формулу для
средней силы
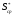 удобно представлять в виде:
удобно представлять в виде:
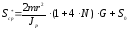 ,
(1П-27)
,
(1П-27)
где
 - число оборотов тела при скатывании с
высоты
- число оборотов тела при скатывании с
высоты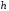 .
.
При
выводе (1П-27) использована соответствующая
(третья) формула для скорости
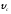 из (1П-3).
из (1П-3).
ПРИЛОЖЕНИЕ 2
ОПРЕДЕЛЕНИЕ ПОТЕРЬ ЭНЕРГИИ ПРИ РЫВКЕ НИТИ
И СКОРОСТИ ЦЕНТРА МАСС ТЕЛА В КОНЦЕ РЫВКА
НА УСТАНОВКЕ МАКСВЕЛЛА
1. Реальные нити не обладают свойствами "идеализированных"
нитей, т.е. абсолютной упругостью и отсутствием деформаций. При каждом
рывке нить получает микроскопическую неупругую деформацию.
Эти деформации, накапливаясь за несколько тысяч рывков, приводят к
Обрыву нити.
Если бы нить имела "идеальные" свойства, тогда скорости центра
масс и угловые скорости тел в начале и конце рывка были бы одинаковы-
ми по величине. Однако неупругая деформация нити приводит к потерям
части кинетической энергии тела, в результате чего скорости в конце
рывка становятся меньше скоростей в начале рывка нити. Это является основ-
ной причиной заметного уменьшения высоты подъёма центра масс тела
при движении "вверх", по сравнению с высотой начального спуска в опытах
на установке Максвелла.
2. Выполним расчёт потерь кинетической энергии за время рывка
нити, полагая известными (из опыта) высоту начального спуска центра масс
при движении тела "вниз", высоту подъёма центра масс при движении
"вверх" после рывка и кинетическую энергию тела в конце спуска (т.е. в нача-
ле рывка нити).
Обозначим: высоту
спуска -
 ,
высоту подъёма -
,
высоту подъёма - ,
кинетическую
,
кинетическую
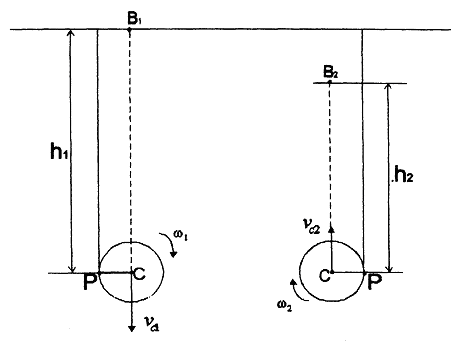
энергию в начале и конце рывка – Т1 и Т2. На рисунке 1-П2 приведена схема,
на
которой показаны: высоты
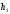 и
и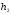 положение тела в начале и в конце рыв-
положение тела в начале и в конце рыв-
ка нити; точки В1 и В2 начального и конечного положений центра масс тела.
|
|
|
начало конец рывка нити рывка нити Рис. 1-П2. |
Запишем уравнения энергетического баланса для спуска и подъёма
тела
с учётом потерь энергии
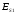 и
и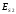 ,
сумма которых (
,
сумма которых (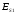 +
+ )
- равна рабо-
)
- равна рабо-
те непотенциальных сил в процессе качения по нити "вниз" и "вверх":

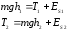 (2П-1)
(2П-1)
Здесь:
 - начальная энергия при движении "вниз";Т2
– началь-
- начальная энергия при движении "вниз";Т2
– началь-
ная
энергия при движении "вверх";
 - масса тела. Из (2П-1) получаем:
- масса тела. Из (2П-1) получаем:
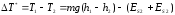 (2П-2)
(2П-2)
Здесь величина
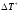 равна потерям энергии за время рывка,
т.к. из разно-
равна потерям энергии за время рывка,
т.к. из разно-
сти потенциальных энергий, определяющей полные потери энергии при движе-
нии от верхней точки В1 начала спуска до верхней точки В2 конца подъёма
центра масс тела, вычитается сумма работ непотенциальных сил в процессе
качения тела по нити.
Преобразуем формулу (2П-2) к другому виду так, чтобы величина
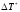 определялась
только величинами
определялась
только величинами
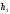 ,
,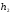 иТ1.
Для этого учтём, что поте-
иТ1.
Для этого учтём, что поте-
ри
энергии
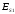 и
и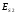 при опускании и подъёме тела должны
при опускании и подъёме тела должны
быть
пропорциональны высотам
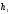 и
и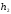 :
:
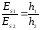 (2П-3)
(2П-3)
Согласно (2П-3), имеем:
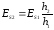 ,
(2П-4)
,
(2П-4)
где:
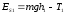 .
.
Подставляя (2П-4)
(с учётом формулы для
 )
в (2П-2), получим иско-
)
в (2П-2), получим иско-
мое выражение:
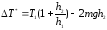 (2П-5)
(2П-5)
Значения
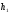 ,
,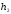 иТ1
определяются
в эксперименте на установке Максвел-
иТ1
определяются
в эксперименте на установке Максвел-
ла.
После вычисления
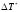 с помощью (2П-5) легко найти величину
кинетиче-
с помощью (2П-5) легко найти величину
кинетиче-
ской энергии тела Т2 в конце рывка:
Т2
=Т1
-
 (2П-6)
(2П-6)
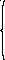 3.
Для расчёта скорости центра масс тела
в конце рывка учтём,
3.
Для расчёта скорости центра масс тела
в конце рывка учтём,
что кинетические энергии Т1 и Т2 определяются формулами:
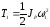 (2П-7)
(2П-7)
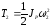 ,
,
где
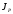 - момент инерции тела относительно оси
в т.Р,
- момент инерции тела относительно оси
в т.Р,
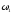 и
и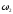 - угло-
- угло-
вые
скорости тела в начальный и конечный моменты времени рывка нити.
Из (2П-7) получаем:
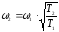 (2П-8)
(2П-8)
Используя формулу Эйлера для скоростей точек тела» вращающего-
ся вокруг оси в т. Р, получим из (2П-8) ещё одно искомое выражение –
для скорости центра масс тела в конце рывка:
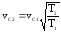 ,
(2П-9)
,
(2П-9)
где
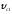 - скорость центра масс в начале рывка,
измеряемая в опыте
- скорость центра масс в начале рывка,
измеряемая в опыте
при скатывании тела из верхнего в нижнее положение.