
Фгбоу впо «калининградский государственный
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
КАФЕДРА ФИЗИКИ
ЛАБОРАТОРНАЯ РАБОТА № 4
ИЗУЧЕНИЕ И ПРИМЕНЕНИЕ ФИЗИЧЕСКОГО И
МАТЕМАТИЧЕСКОГО МАЯТНИКОВ
Методическое указание к выполнению лабораторной работы по разделу «Механика» для студентов всех форм обучения по всем специальностям
Калининград
2001
1. ЦЕЛЬ РАБОТЫ
1.1. Ознакомление с физическим и математическим маятниками, изучение периодического движения маятников как примера колебаний в системах с одной степенью свободы.
1.2. Измерение ускорения силы тяжести с помощью математического маятника.
1.3. Измерение периода колебаний физического маятника и сравнение его с расчётным значением.
1.4. Измерение момента инерции тела сложной формы с помощью физического маятника.
ИСПОЛЬЗУЕМЫЙ РЕКВИЗИТ: груз, ручной секундомер (при необходимости).
2. Введение
Колебаниями называются периодические изменения состояния некоторой системы, обладающей положением устойчивого равновесия (покоя) и характеризующейся собственной частотой колебаний.
Частным случаем (и наиболее наглядным) являются механические системы (устройства), в которых могут возникать периодические движения (поступательное, вращательное, плоское и т.д.), т.е. колебания, когда через равные интервалы времени повторяются значения координат, скоростей, ускорений, энергий и т.п. тел (точек), образующих данную систему.
Если положение механической системы в пространстве можно определить с помощью одного параметра (линейной либо угловой координаты), тогда такая система называется системой с одной степенью свободы.
В данной работе будут рассмотрены механические системы с одной степенью свободы, обладающие положением устойчивого равновесия и собственной частотой колебаний.
Частотой(обыкновенной) νо
называется число одинаковых состояний
в единицу времени. Единица измерения
ν0-Гц. Однако при изучении
колебаний оказывается удобным использовать
также другой интервал времени Δt = 2π
сек. и, соответственно, применять другое
значение частоты КО, как числа одинаковых
состояний за время 2π сек. Частота КО
называется собственной циклической
частотой данной системы, её размерность
[К0] =c-1и она связана с
частотойν0соотношениемК0
= 2π ν0. Необходимость
введения двух значений частот объясняется
тем, что обыкновенную частотуν0можно найти из опыта, измеряя число
одинаковых состояний на некотором
промежутке времени; циклическую частотуК0можно вычислить теоретически,
зная параметры системы.Периодом
колебанийТ0называется
интервал времени между двумя ближайшими
одинаковыми состояниями. Очевидно: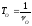 cи
cи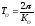 c.
c.
Физическим
маятникомназывается устройство,
содержащее твёрдое тело, подвешенное
в гравитационном поле на оси, не проходящей
через центр масс тела (рис. 1).
d φ D- точка на оси подвеса С - центр
масс |DC|
= l d
- плечо силы C D Рис.
1
















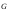
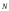
Однако, если тело отклонить на некоторый угол φ(показан на рис. 1), тогда появляется момент силы тяжести, численно равный
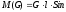 φ,
φ,
где
 φ
=d(момент силы
реакции остается нулевым, т.к. эта сила
приложена в точке подвеса).
φ
=d(момент силы
реакции остается нулевым, т.к. эта сила
приложена в точке подвеса).
Учитывая
направления проекции вектора момента
 ,
получаем следующее уравнение вращательного
движения тела вокруг оси в точкеD:
,
получаем следующее уравнение вращательного
движения тела вокруг оси в точкеD:
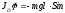 φ,
(1)
φ,
(1)
где
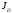 - момент инерции тела относительно оси
подвеса;
- момент инерции тела относительно оси
подвеса;
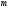 - масса тела;
- масса тела;
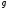 - ускорение силы тяжести.
- ускорение силы тяжести.

Будем считать угол отклонения φмалым, чтобы выполнялось условие
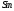 φ
≈ φ
φ
≈ φ
Тогда уравнение (1) запишется в виде:
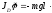 φ
(2)
φ
(2)
Преобразуем уравнение (2), перенося все его члены в левую часть и разделив на коэффициент при первом члене:
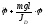 = 0 (3)
= 0 (3)
Обозначим:
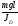 =К02
=К02
и получим
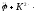 φ
= 0 (3а)
φ
= 0 (3а)
В математике уравнения типа (3а) называются линейными дифференциальнымиуравнениями второго порядка с постоянными коэффициентами.Заметим, что линейность этого уравнения в данном случае обусловлена малостью отклонений от положения устойчивого равновесия. В теории дифференциальных уравнений доказано, что решением уравнения (3а) является функция
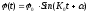 ,
(4)
,
(4)
где
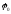 - амплитуда (максимальное смещение от
положения равновесия);
- амплитуда (максимальное смещение от
положения равновесия);
 - начальная фаза, т.е. параметр,
характеризующий начальное положение
тела;
- начальная фаза, т.е. параметр,
характеризующий начальное положение
тела;
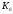 - собственная циклическая частота
колебаний.
- собственная циклическая частота
колебаний.
Подчеркнём, что частота
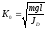 может быть вычислена заранее, если
известны момент инерции, масса и положение
центра масс тела.
может быть вычислена заранее, если
известны момент инерции, масса и положение
центра масс тела.
Согласно
выражению (4) угол поворота
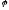 будет периодически изменяться с течением
времени, т.е. тело, подвешенное, как
показано на рис. 1, начнет поочерёдно
отклоняться то влево, то вправо от
вертикали, повторяя свои положения
через равные промежутки времени. Таким
образом, возникают колебания, в процессе
которых будут повторяться также значения
угловых скоростей и ускорений, кинетической
и потенциальной энергий и т.д. Само же
тело при этом совершает частный вид
механического движения - вращение вокруг
оси подвеса.
будет периодически изменяться с течением
времени, т.е. тело, подвешенное, как
показано на рис. 1, начнет поочерёдно
отклоняться то влево, то вправо от
вертикали, повторяя свои положения
через равные промежутки времени. Таким
образом, возникают колебания, в процессе
которых будут повторяться также значения
угловых скоростей и ускорений, кинетической
и потенциальной энергий и т.д. Само же
тело при этом совершает частный вид
механического движения - вращение вокруг
оси подвеса.
Математическим маятником называется некоторое идеализированное устройство, содержащее материальную точку, подвешенную в гравитационном поле на жёстком невесомом стержне, способном вращаться на оси, проходящей через точку подвеса.
Очевидно, что математический маятник - это частный случай физического маятника при условии, что центр массы подвешенного тела расположен в его нижней точке. Следовательно, момент инерции в такой конструкции равен
J=ml2 , гдеl - расстояние до оси подвеса.
Уравнение (3) запишется в виде:
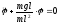
или
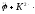 φ
= 0, (5)
φ
= 0, (5)
где
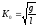
Решением уравнения (5) попрежнему будет функция вида (4). Но при этом частота К0определяется только длинойl, т.е. расстоянием от оси подвеса до точки, где сосредоточена масса системы.
