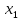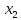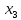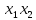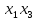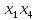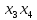Лабораторная работа № 1
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФГБОУ ВПО «Поволжский государственный технологический университет»
Кафедра ПиП ЭВС
Отчет по лабораторной работе № 1
«Построение модели технологического процесса методом планирования эксперимента»
по дисциплине «МММ»
Вариант 7
Выполнил: ст. гр. ЭиНЭм-11
Поздеев Ю. В.
Проверил: профессор
Ю. В. Захаров
Йошкар-Ола
2013
Цель работы: практическое освоение методики построения математической модели технологического процесса методом планирования эксперимента.
Основные теоретические сведения
Математическая модель технологического процесса - это аналитическое выражение зависимости показателя качества изготавливаемого изделия от факторов, определяющих его численную величину.
Математическое моделирование позволяет решать следующие технологические задачи:
-
оптимизация режимов проведения технологического процесса;
-
оценка и прогнозирование состояния технологического процесса;
-
управление технологическим процессом.
Для этого применяют экспериментально-статистические методы:
-
корреляционно-регрессионный анализ;
-
планирование активного эксперимента (ПАЭ).
Алгоритм построения математической модели технологического процесса методом ПАЭ имеет следующие этапы:
-
выбор плана эксперимента;
-
реализацию плана эксперимента, вычисление коэффициентов модели, проверку адекватности модели;
-
анализ полученной модели и принятие решения по модели.
Построение матриц планирования ПФЭ 24 с парными взаимодействиями 4-х факторов
При моделировании применяют план полного факторного эксперимента типа 24. Запись 24 говорит о том, что факторы фиксируются на 2-х уровнях, а число факторов равно 4. Матрица плана ПФЭ 24 приведена в таблице 1. Число опытов вычисляется по формуле N=24. Для нашего случая N=24=16. Опыты 17-20 являются дополнительными и служат для вычисления дисперсии воспроизводимости экспериментов (S2 восп.)
Общее выражение математической модели с учетом парных взаимодействий факторов х1, х2, х3, х4 имеет следующий вид:
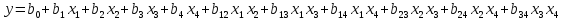 (1)
(1)
Таблица 1
Матрица планирования эксперимента ПФЭ 24
|
№ опыта |
|
|
|
|
|
|
|
|
|
|
y |
|
1 |
-1 |
-1 |
-1 |
-1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+ 1 |
12 |
|
2 |
+1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
+1 |
+1 |
+ 1 |
11 |
|
3 |
-1 |
+1 |
-1 |
-1 |
-1 |
+1 |
+1 |
-1 |
-1 |
+ 1 |
12 |
|
4 |
+1 |
+1 |
-1 |
-1 |
+1 |
-1 |
-1 |
-1 |
-1 |
+ 1 |
10 |
|
5 |
-1 |
-1 |
+1 |
-1 |
+1 |
-1 |
+1 |
-1 |
+1 |
-1 |
14 |
|
6 |
+1 |
-1 |
+1 |
-1 |
-1 |
+1 |
-1 |
-1 |
+1 |
-1 |
13 |
|
7 |
-1 |
+1 |
+1 |
-1 |
-1 |
-1 |
+1 |
+1 |
-1 |
-1 |
13 |
|
8 |
+1 |
+1 |
+1 |
-1 |
+1 |
+1 |
-1 |
+1 |
-1 |
-1 |
12 |
|
9 |
-1 |
-1 |
-1 |
+1 |
+1 |
+1 |
-1 |
+1 |
-1 |
-1 |
13 |
|
10 |
+1 |
-1 |
-1 |
+1 |
-1 |
-1 |
+1 |
+1 |
-1 |
-1 |
13 |
|
11 |
-1 |
+1 |
-1 |
+ 1 |
-1 |
+1 |
-1 |
-1 |
+1 |
-1 |
10 |
|
12 |
+1 |
+1 |
-1 |
+1 |
+1 |
-1 |
+1 |
-1 |
+1 |
-1 |
15 |
|
13 |
-1 |
-1 |
+1 |
+1 |
+1 |
-1 |
-1 |
-1 |
-1 |
+ 1 |
10 |
|
14 |
+1 |
-1 |
+1 |
+ 1 |
-1 |
+1 |
+1 |
-1 |
-1 |
+ 1 |
14 |
|
15 |
-1 |
+1 |
+1 |
+ 1 |
-1 |
-1 |
-1 |
+1 |
+1 |
+ 1 |
16 |
|
16 |
+1 |
+1 |
+1 |
+ 1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+ 1 |
13 |
|
17 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
12 |
|
18 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
13 |
|
19 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
14 |
|
20 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
12 |
Вычисление коэффициентов модели
После построения матрицы планирования ПФЭ 24 коэффициенты модели b0, b1,…,b34 вычисляем по формулам:
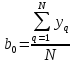 (2)
(2)
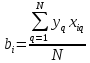 (3)
(3)
 (4)
(4)
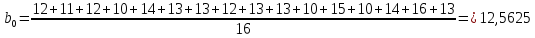
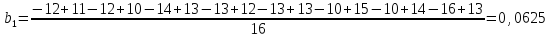
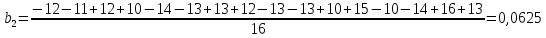
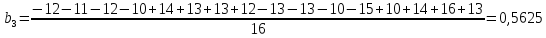
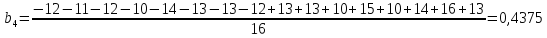
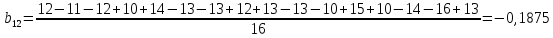
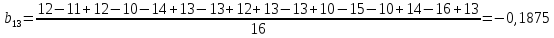
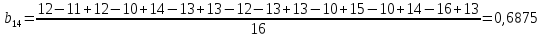
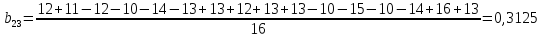
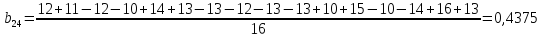
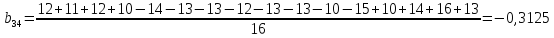
Проверка значимости коэффициентов модели
Проверка значимости коэффициентов модели осуществляется по t- критерию Стьюдента. Для этого вычислим дисперсию воспроизводимости, используя опыты 17-20 из таблицы 1.
 (5)
(5)
где
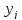 – результат j-го
опыта;
– результат j-го
опыта;
 – среднее
значение из n
опытов
(n=4
– число повторных опытов);
– среднее
значение из n
опытов
(n=4
– число повторных опытов);
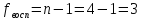 ;
;

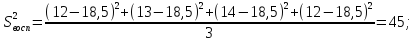
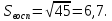
Вычислим tрасч для каждого коэффициента модели по формуле:
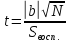 (6)
(6)
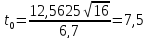
Аналогично найдем tрасч для остальных коэффициентов модели:

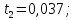

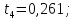


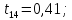
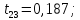
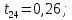
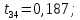
Табличное
значение при α=0,05:

Коэффициенты
модели значимые с вероятностью 95%, если
tрасч
>
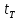
Исключив незначимые коэффициенты, получим математическую модель в виде:
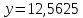 (7)
(7)
Проверка адекватности полученной модели
Проверка осуществляется по F-критерию Фишера.
Определятся остаточная дисперсия, характеризующая рассеяние экспериментальных данных относительно результатов, полученных по найденной математической модели:
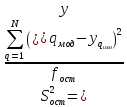 (8)
(8)
где
 – показатель качества для q-ого
опыта при подстановке в модель (7) величин
– показатель качества для q-ого
опыта при подстановке в модель (7) величин
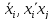 из таблицы 1 и вычисленных значимых
коэффициентов
из таблицы 1 и вычисленных значимых
коэффициентов
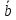 ;
;
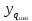 -
экспериментально полученное значение
-
экспериментально полученное значение
 в q-ом
опыте. Значения
в q-ом
опыте. Значения
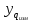 приведены в таблице 1 (последний столбец,
опыты 1-16);
приведены в таблице 1 (последний столбец,
опыты 1-16);
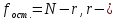 общее
число значимых коэффициентов модели,
включая и коэффициент
общее
число значимых коэффициентов модели,
включая и коэффициент
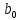 .
.
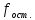 =
16-1=15.
=
16-1=15.
Найдем
значения
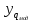 по полученной математической модели:
по полученной математической модели:
у = 12,5625
Тогда
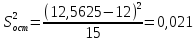
Вычислим отношение Фишера по формуле:
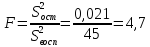
Находим
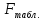 при α=0,05,
при α=0,05,
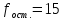 ,
,
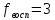 :
:
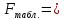 8,7.
8,7.
Сравним
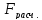 и
и
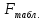
Вывод: Так как 4,7<8,7, то с вероятностью 95% математическая модель является адекватной.