7.Корелляционно-регрессионный анализ

На основании произведенных расчетов проведем корреляционно-регрессионный анализ

Форма уравнения регрессии – линейная.

График зависимости результативного признака от факторного, составленный по исходным данным

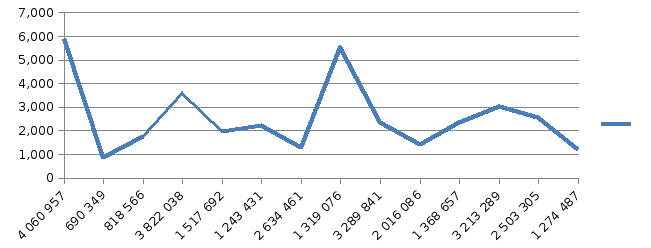
Для наших данных система уравнений имеет вид

14a + 29772235 b = 36148

29772235 a + 79752791962413 b = 87845437210

Из первого уравнения выражаем а и подставим во второе уравнение:

Получаем эмпирические коэффициенты регрессии: b = 0.000668, a = 1162.5024

Уравнение регрессии (эмпирическое уравнение регрессии):

y = 0.000668 x + 1162.5024

x	y	x2	y2	x • y
4060957	5907	16491371755849	34892649	23988072999
690349	876	476581741801	767376	604745724
818566	1779	670050296356	3164841	1456228914
3822038	3589	14607974473444	12880921	13717294382
1517692	1994	2303389006864	3976036	3026277848
1243431	2240	1546120651761	5017600	2785285440
2634461	1284	6940384760521	1648656	3382647924
1319076	5532	1739961493776	30603024	7297128432
3289841	2358	10823053805281	5560164	7757445078
2016086	1426	4064602759396	2033476	2874938636
1368657	2363	1873221983649	5583769	3234136491
3213289	3049	10325226197521	9296401	9797318161
2503305	2558	6266535923025	6543364	6403454190
1274487	1193	1624317113169	1423249	1520462991
29772235	36148	79752791962413	123391526	87845437210

Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:

В нашем примере связь между признаком Y фактором X умеренная и прямая.

Уравнение регрессии (оценка уравнения регрессии).

Линейное уравнение регрессии имеет вид y = 0.000668 x + 1162.5

Коэффициент регрессии b = 0.000668 показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 0.000668. В нашем примере связь прямая.

. Коэффициент эластичности.

Средний коэффициент эластичности E показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения.

Коэффициент эластичности находится по формуле:

Коэффициент эластичности меньше 1. Следовательно, при изменении Х на 1%, Y изменится менее чем на 1%. Другими словами - влияние Х на Y не существенно.

Бета – коэффициент

Т.е. увеличение x на величину среднеквадратического отклонения S_x приведет к увеличению среднего значения Y на 0.49 среднеквадратичного отклонения S_y.

Ошибка аппроксимации.

Поскольку ошибка больше 7%, то данное уравнение не желательно использовать в качестве регрессии.

Эмпирическое корреляционное отношение.

где

Индекс корреляции.

Для линейной регрессии индекс корреляции равен коэффициенту корреляции r_xy = 0.49.

Полученная величина свидетельствует о том, что фактор x умеренно влияет на y

Для любой формы зависимости теснота связи определяется с помощью множественного коэффициента корреляции:

Данный коэффициент является универсальным, так как отражает тесноту связи и точность модели, а также может использоваться при любой форме связи переменных. При построении однофакторной корреляционной модели коэффициент множественной корреляции равен коэффициенту парной корреляции r_xy.

Коэффициент детерминации.

R²= 0.49² = 0.2437

т.е. в 24.37 % случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - низкая. Остальные 75.63 % изменения Y объясняются факторами, не учтенными в модели (а также ошибками спецификации).

Для оценки качества параметров регрессии построим расчетную таблиц

x	y	y(x)	(yi-ycp)2	(y-y(x))2	(xi-xcp)2	|y - yx|:y
4060957	5907	3873.19	11055625	4136378.38	3741782599145.8	0.34
690349	876	1623.31	2910436	558472.72	2062783080652	0.85
818566	1779	1708.9	644809	4914.69	1710922113064.9	0.0394
3822038	3589	3713.71	1014049	15553.27	2874549975878.7	0.0347
1517692	1994	2175.56	345744	32964.68	370754599771.47	0.0911
1243431	2240	1992.49	116964	61259.93	779966665144.9	0.11
2634461	1284	2921.01	1684804	2679785.65	257934766469.19	1.27
1319076	5532	2042.99	8702500	12173221.5	652075976220.61	0.63
3289841	2358	3358.47	50176	1000942.69	1353157043472.1	0.42
2016086	1426	2508.24	1336336	1171242.92	12210739362.04	0.76
1368657	2363	2076.08	47961	82322.56	574459725588.61	0.12
3213289	3049	3307.37	218089	66756.49	1180918597672.1	0.0847
2503305	2558	2833.46	576	75877.36	141915536638.91	0.11
1274487	1193	2013.22	1929321	672764.85	726076479387.18	0.69
29772235	36148	36148	30057390	22732457.69	16439507898468	5.56

Значимость коэффициента корреляции.

t_крит (n-m-1;α/2) = (12;0.025) = 2.179

Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим

Интервальная оценка для коэффициента корреляции (доверительный интервал).

Доверительный интервал для коэффициента корреляции

r(0.0532;0.93)

Дисперсионный анализ.

∑(y_i - y_cp)² = ∑(y(x) - y_cp)² + ∑(y - y(x))²

Источник вариации	Сумма квадратов	Число степеней свободы	Дисперсия на 1 степень свободы	F-критерий
Модель	7324932.31	1	7324932.31	3.87
Остаточная	22732457.69	12	1894371.47	1
Общая	30057390	14-1

Показатель	Значение
Коэффициент детерминации	0.24
Средний коэффициент эластичности	0.55
Средняя ошибка аппроксимации	39.74