МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНО-ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ» МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ Кафедра высшей математики
Реферат по дисциплине «Проективная геометрия»
Проективные преобразования прямой и плоскости
		Работу выполнила студентка 131 группы Юдина Александра Викторовна ________________ подпись
Оценка за реферат ______________________		Проверила канд. физ.-мат. наук, доцент, Миляуша Сабитовна Ананьева _______________ подпись
	Пермь 2013

Содержание

Введение 2

1. Проективные преобразования прямой 2

2. Проективные преобразования плоскости 5

Заключение 7

Список литературы 7

2.Певзнер С. Л. Проективная геометрия. – М.: Просвещение, 1980. – 61 с. 7

3.Хартсхорн Р. Основы проективной геометрии. – М.: Мир, 1970 г. – 71-84 с. 7

Введение

Цель – изучить проективные преобразования прямой и плоскости.

Задачи:

1) Проанализировать литературу по теме;

2) Выделить основные определения и теоремы;

3) Привести задачи с решениями.

1. Проективные преобразования прямой

Проективным преобразованием прямой g называется преобразование, при котором сохраняется двойное отношение произвольных четырех точек. Наиболее простым примером проективного преобразования прямой является тождественное преобразование, то есть преобразование, в котором каждая точка переходит в себя.

Теорема. Пусть на проективной прямой заданы две упорядоченные тройки точек, причем в каждой тройке все точки различны. Тогда существует единственное проективное преобразование прямой, отображающее первую тройку во вторую.

Следствие: Проективное преобразование прямой, отличное от тождественного, может иметь не более двух неподвижных точек.

Рассмотрим задачи построения образов точек при проективном преобразовании прямой.

Задача 1. В проективном отображении f: g→g репер R=(A, B, C) переходит в репер R=(A, B, C). Построить образ произвольной точки прямой g.

Решение: Для решения задачи попытаемся представить отображение f как произведение двух перспективных отображений. Проведем прямую АА и возьмем на ней две точки О и О, отличные от точек А и А. Пусть В₀ – точка пересечения прямых ОВ, ОВ, а С₀ – точка пересечения прямых ОС и ОС (рис. 1). Обозначим через g₀ прямую В₀С₀ и рассмотрим перспективное отображение f₁: g→g₀ с центром в точке О и другое перспективное отображение f₂:g₀→g с центром в точке О. Отображение f₁f₂: g→g переводит точки А, В, С соответственно в точки А, В, С, поэтому они совпадают с отображением f, то есть f=f₂f₁.

Отсюда следует простой способ построения образа М произвольной точки М прямой g:

1) (ОМ);

2) М₀=(ОМ) g₀;

3) (М₀О);

4) М=(M₀O) g.

В самом деле, М₀=f₁(M), M=f₂(M₀), поэтому f(M)=f₂f₁(M)=f₂(M₀)=M.

Рис. 1

Задача 2. При проективном преобразовании f: g→g репер R=(A, B, C) переходит в репер R=(A, B, C). Построить образ произвольной точки М и прямой g.

Решение: Проведем какую-нибудь прямую g₁, отличную от прямой g, и возьмем точку Р, не лежащую на прямых g и g₁. Построим образы точек А, В, С и М в перспективном отображении f₁: g→g₁ с центром Р (на рис. 2 образы этих точек обозначены через А₁, В₁, С₁, М₁). Затем построим образ точки М в проективном отображении f₂: g₁→g, которое репер (А₁, В₁, С1) переводит в репер (А, В, С) (задача 1).

Ясно, что f₂f₁ – проективное преобразование прямой g, которое переводит репер R в репер R, поэтому f₂f₁= f. Отсюда следует, что М – искомая точка, так как f(M)=f₂f₁(M)=f₁(M₁)=M.

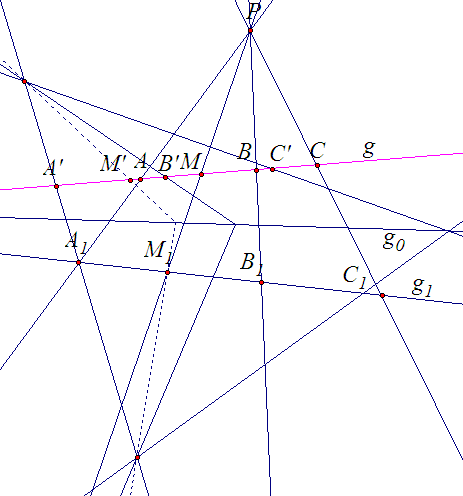
Рис. 2

2. Проективные преобразования плоскости

По определению проективная плоскость представляет собой множество точек и прямых, поэтому проективное преобразование может отображать точки – на точки, прямые – на прямые.

Однако возможны и такие преобразования, при которых образом точки будет прямая, а образом прямой – точка. Следовательно, имеются два типа проективных преобразований в зависимости от того, переводят ли они элементы проективной плоскости какого-либо вида в элементы того же или другого вида.

Преобразования первого вида, отображающие прямые в прямые, а точки – в точки, называются коллинеациями, преобразования второго типа, отображающие прямые в точки, а точки в прямые, называются корреляциями.

Гомологией называется нетождественная коллинеация, для которой существует точечно неподвижная прямая (все ее точки неподвижны при некотором преобразовании), называемая осью гомологии.

Теорема. Для всякой гомологии существует неподвижная точка (центр гомологии), обладающая тем свойством, что каждая инцидентная ей прямая неподвижна. Кроме центра и точек оси, гомология неподвижных точек не имеет.

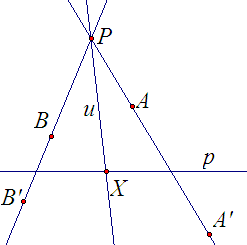
Если р – ось гомологии, Ар – какая-либо точка, А=(А), Р – центр гомологии, тогда

а) Р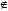р (гиперболическая гомология). В этом случае всякая прямая u, проходящая через Р, неподвижна , так как имеет две неподвижные точки – точку Р и точку Х=u∩p (рис. 3).

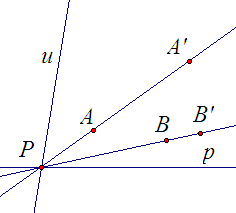
б) Рр (параболическая гомология). В этом случае всякая прямая u, проходящая через Р, неподвижна потому, что она и ее образ должны составлять одно и тоже двойное отношение с тремя прямыми ˗ р, АА, ВВ(рис. 4).

Рис. 3	Рис. 4

Заключение

В ходе выполнения работы была изложена обобщенная информация по теме (определения, теоремы, сопровожденные иллюстрациями); приведены задачи с решениями.

Таким образом, цель, поставленная перед началом работы, достигнута.

Список литературы

1. Атанасян Л. С., Базылев В. Г. Геометрия. Учебное пособие для студентов физ.-мат. фак. пед.ин-тов. В 2ч. Ч. 2. – М.: Просвещение, 1987. – 49 с.

2. Певзнер С. Л. Проективная геометрия. – М.: Просвещение, 1980. – 61 с.

3. Хартсхорн Р. Основы проективной геометрии. – М.: Мир, 1970 г. – 71-84 с.