
Практика №3
.docxПрактическая работа №5
Тема: Степени с рациональным показателем и их свойствами
Цель: формирование навыков нахождения степени с рациональным показателем
Вид работы: индивидуальный
Время выполнения: 2 часа
Теоретические сведения
Рассмотрим степень
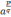
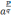 ,
где
,
где 
 – рациональное число. Выражение
– рациональное число. Выражение 
 имеет в общем виде смысл только при
имеет в общем виде смысл только при
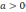
 .
Если
.
Если 
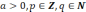 ,
то по определению
,
то по определению 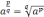
 ;
;
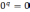
 .
.
Степень с рациональным
показателем обладает теми же свойствами,
что и степень с натуральным показателем,
а именно если 
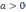 и
и 
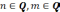 ,
то:
,
то:
а) 
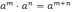 ;
;
б)

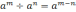 ;
;
в) 
 ;
;
г) 
 ;
;
д)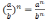
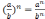 .
.
Пример 1. Упростить выражение:
-
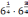
 ;
2)
;
2) 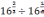
 ;
3)
;
3) 
 ;
4)
;
4)
 ;
5)
;
5) 
 .
.
Решение.
1) 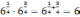
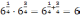 ;
;
-
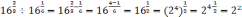
 ;
;
-

 .
.
Практическая работа №6
Тема: Степени с действительным показателем и их свойства
Цель: формирование навыков нахождения степени с рациональным показателем
Вид работы: индивидуальный
Время выполнения: 2 часа
Теоретические сведения
Теорема.
Пусть 
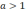 и
и 
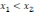 .
Тогда
.
Тогда 
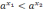 .
.
Следствие 1.
Пусть 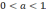
 и
и 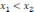
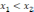 .
Тогда
.
Тогда 
 .
.
Упражнения с решениями
Пример 1.
Упростить выражение 
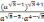 .
.
Решение. Применяя свойства степени с действительным показателем, получаем
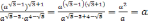
 .
.
Пример 2.
Сравнить числа 
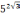 и
и 
 .
.
Решение.
Сравним показатели 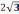
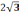 и
и 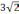
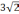 .
Так как
.
Так как 
 ,
,

 и
и 
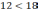 ,
то
,
то 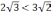
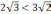 .
Поэтому
.
Поэтому 
 .
.
Пример 3.
Сравнить числа 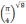
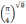 и
и 
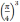 .
.
Решение.
Так как 
 ,
то
,
то 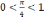
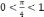 .
Сравним показатели: так как
.
Сравним показатели: так как 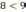
 ,
то
,
то 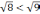
 ,
т.е.
,
т.е. 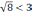
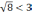 .
Применяя следствие 1, получаем, что
.
Применяя следствие 1, получаем, что 
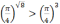 .
.
Пример 4.
Решить уравнение 
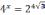 .
.
Решение.
По свойства степени 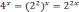
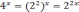 .
Поэтому уравнение можно записать так:
.
Поэтому уравнение можно записать так:

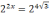 .
Применяя следствие 2, получаем
.
Применяя следствие 2, получаем 
 ,
откуда
,
откуда 
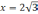 .
.
Задания к практической работе 3
Задание 1. Вычислите:
-
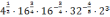
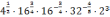 ;
; -

 .
. -
.
Задание 2. Вычислите:
-
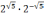
 ;
; -
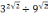
 ;
; -
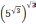
 ;
; -

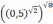 .
.
Задание 3. Вычислите:
-

 ;
; -

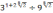 ;
; -
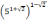
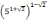 ;
; -

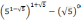 ;
; -

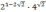 ;
; -

 ;
;
Задание 4. Выясните, какое из чисел больше:
-
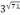
 или
или 
 ;
; -
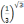
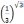 или
или
 ;
; -
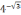
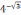 или
или 
 ;
; -
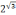
 или
или 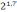
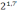 ;
; -
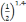
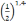 или
или 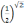
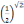 ;
; -
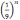
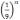 или
или 
 .
.
