2. Предел и непрерывность функции нескольких переменных

Рассмотренные выше понятия функций двух или трех переменных можно обобщать на случай переменных.

Определение. Функцией переменныхназывается функция, область определениякоторой принадлежит, а область значений – действительной оси.

Такая функция каждому набору переменных изсопоставляет единственное число.

В дальнейшем для определенности мы будем рассматривать функции переменных, но все утверждения сформулированные для таких функции остаются верными и для функций большего числа переменных.

Определение. Число называется пределом функции

в точке , если для каждогонайдется такое числочто при всехиз окрестности, кроме этой точки, выполняется неравенство

.

Если предел функции в точкеравен, то это обозначается в виде

.

Практически все свойства пределов рассмотренные нами ранее для функций одной переменной остаются справедливыми и для пределов функций нескольких переменных, однако практическим нахождением таких пределов мы заниматься не будем.

Определение. Функция называется непрерывной в точкеесли выполняется три условия:

1) существует

2) существует значение функции в точке

3) эти два числа равны между собой, т.е. .

Практически исследовать непрерывность функции можно с помощью следующей теоремы.

Теорема. Любая элементарная функция непрерывна во всех внутренних (т.е. не граничных) точках своей области определения.

Пример. Найдем все точки, в которых функция

непрерывна.

Как было отмечено выше, эта функция определена в замкнутом круге

.

Внутренние точки этого круга является искомыми точками непрерывности функции, т.е. функция непрерывна в открытом круге.

Определение понятия непрерывности в граничных точках области определения функции возможно, но мы этот вопрос в курсе затрачивать не будем.

1.3 Частные приращения и частные производные

В отличие от функций одной переменной, функций нескольких переменных имеют различные виды приращений. Это связано с тем, что перемещения в плоскости из точкиможно осуществлять по различным направлениям.

Определение. Частным приращением по функциив точкесоответствующим приращениюназывается разность

.

Это приращение по существу является приращением функции одной переменной полученной из функциипри постоянном значении.

Аналогично частным приращением по в точке функциисоответствующим приращениюназывается разность

.

Это приращение вычисляется при фиксированном значении .

Пример. Пусть ,,. Найдем частные приращения этой функции пои по

.

В данном примере при равных значениях приращений аргументов и, частные приращения функции оказались различными. Это связано с тем, что площадь прямоугольника со сторонамиипри увеличении сторонынаувеличивается на величину, а при увеличении сторонынаувеличивается на(см.рис.4).

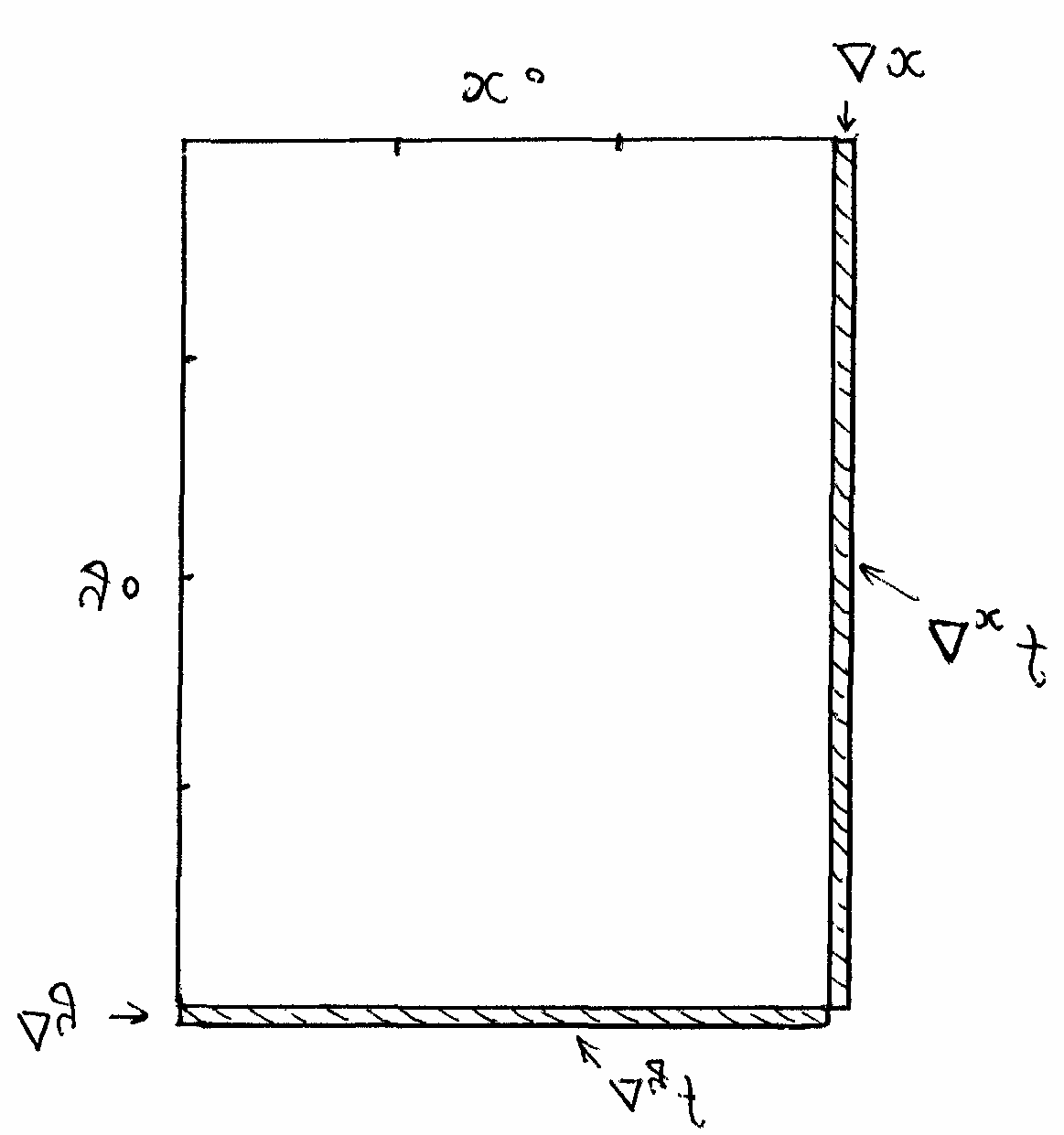
Рис.4.

Из того факта, что функция двух переменных имеет два вида приращений, следует, что для нее можно определить два вида производных.

Определение. Частной производной по функциив точкеназывается предел отношения частного приращения поэтой функции в указанной точке к приращениюаргументат.е.

. (1)

Такие частные производные обозначаются символами ,,,. В последних случаях круглая буква “” – “” означает слово “частная”.

Аналогично, частная производная по в точкеопределяется с помощью предела

. (2)

Другие обозначения этой частной производной: ,,.

Частные производные функций находятся по известным правилам дифференцирования функции одной переменной, при этом все переменные, кроме той, по которой дифференцируется функция, считаются постоянными. Так при нахождении переменнаяпринимается за постоянную, а при нахождении- постоянная.

Пример. Найдем частные производные функции .

, .

Пример. Найдем частные производные функции трех переменных

.

; ;.

Частные производные функции характеризуют скорости изменения этой функции в случае, когда одна из переменных фиксируется.

Пример по экономики.

Основным понятием теории потребления является функция полезности . Эта функция выражает меру полезности набора, где х- количество товара Х, у - количество товара У. Тогда частные производныебудут соответственно называться предельными полезностями х и у. Предельная норма замещенияодного товара другим равна отношению их предельных полезностей:

. (8)

Задача 1. Найти предельную норму замещения ч на у для функции полезности в точке А(3,12).

Решение: по формуле (8) получаем

Экономический смысл предельной нормы замещения заключается в обосновании формулы , где-цена товара Х,- цена товара У.

Определение. Если у функции имеются частные производные, то ее частными дифференциалами называются выражения

и

здесь и.

Частные дифференциалы являются дифференциалами функций одной переменной полученных из функции двух переменных при фиксированныхили.

Примеры из экономики. Рассмотрим в качестве примера функцию Кобба-Дугласа.

Величина - средняя производительность труда, так как это количество продукции (в стоимостном выражении), произведенное одним рабочим.

Величина - средняя фондоотдача- количество продукции, приходящееся на один станок.

Величина - средняя фондовооруженность- стоимость фондов, приходящееся на единицу трудовых ресурсов.

Поэтому частная производная называется предельной производительностью труда, так как она равна добавочной стоимости продукции, произведенной еще одним дополнительным рабочим.

Аналогично, - предельная фондоотдача.

В экономике часто задают вопросы: на сколько процентов изменится выпуск продукции, если число рабочих увеличить на 1% или если фонды возрастут на 1%? Ответы на такие вопросы дают понятия эластичности функции по аргументу или относительная производная. Найдем эластичность выпуска продукции по труду . Подставляя в числитель вычисленную выше частную производную, получим. Итак, параметримеет ясный экономический смысл – это эластичность выпуска по труду.

Аналогичный смысл имеет и параметр - это эластичность выпуска по фондам.