
- •Лекция 2 Производная по направлению градиент. Производные и дифференциалы высших порядков. Экстремумы функции нескольких переменных и задачи оптимизации в экономике Вопросы.
- •Дифференцируемость функции нескольких переменных
- •2. Уравнение касательной плоскости и нормали к поверхности
- •3. Производная по направлению и градиент функции нескольких переменных.
- •4. Производная высших порядков
- •5. Экстремум функции нескольких переменных
- •Пусть функция трижды дифференцируема в некоторой окрестности своей критической точки.
- •Литература
Лекция 2 Производная по направлению градиент. Производные и дифференциалы высших порядков. Экстремумы функции нескольких переменных и задачи оптимизации в экономике Вопросы.
Дифференцируемость функции нескольких переменных.
Геометрический смысл дифференциала 1-ого порядка.
Уравнение касательной плоскости и нормали.
Производная по направлению, определение.
Что такое градиент функции
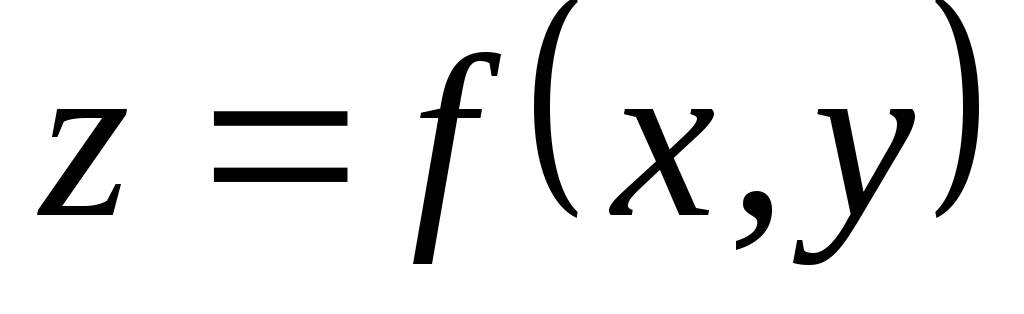 в заданной точке?
в заданной точке?Производные и дифференциалы высших порядков.
Необходимое условие локального экстремума.
Сформулируйте достаточное условие локального максимума в точке
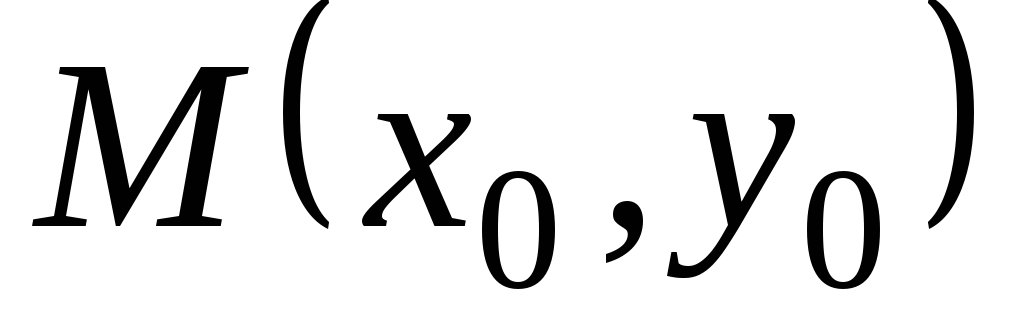 функции
функции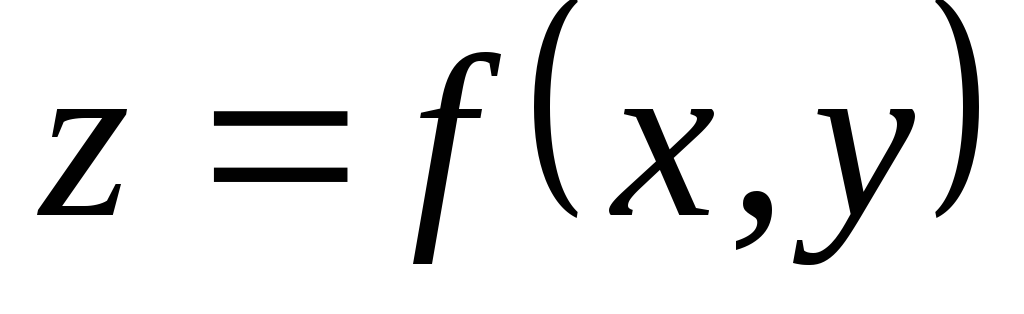 .
.Задачи оптимизации в экономике.
Дифференцируемость функции нескольких переменных
При полном приращении функции, в отличие от частных приращений могут изменяться все переменные функции нескольких переменных.
Определение.Полным приращением
функции![]() в точке
в точке![]() ,
соответствующим приращениям
,
соответствующим приращениям![]() и
и![]() аргументов, называется разность
аргументов, называется разность
![]() .
.
Пример.Пусть![]() ,
,![]() ,
,![]() ,
,![]() (см. пример из предыдущего пункта). Найдем
полное приращение функции в точке
(см. пример из предыдущего пункта). Найдем
полное приращение функции в точке![]() :
:
![]()
Это
приращение равно приращению площади
прямоугольника со сторонами 3 и 4 при их
увеличении на величины, равные 0,1. На
рис.4 полное приращение
![]() состоит из площадей двух заштрихованных
прямоугольников и площади квадрата со
стороной 0,1.
состоит из площадей двух заштрихованных
прямоугольников и площади квадрата со
стороной 0,1.
Определение.Если полное приращение
функции![]() в точке
в точке![]() можно записать в виде:
можно записать в виде:
![]() ,
где
,
где![]() и
и![]() – постоянные, а
– постоянные, а![]() и
и![]() бесконечно малые при
бесконечно малые при![]() ,
то выражение
,
то выражение
![]()
называется полным дифференциалом
функции в точке
![]() .
.
Полный дифференциал называют также главной частью приращения функции.
Функция, имеющая полный дифференциал в некоторой точке, называется дифференцируемой в этой точке.
Теорема 1. Пусть функция![]() и ее частные производные
и ее частные производные![]() и
и![]() непрерывны в некоторой окрестности
точки
непрерывны в некоторой окрестности
точки![]() .
Тогда функция
.
Тогда функция![]() дифференцируема в т.
дифференцируема в т.![]() и ее полный дифференциал равен сумме
частных дифференциалов:
и ее полный дифференциал равен сумме
частных дифференциалов:
![]() .
(3)
.
(3)
Пример.Найдем полный дифференциал
функции![]() .
.
Найдем вначале частные производные этой функции:
![]() ;
;![]() .
.
Подставив их в формулу (2), получим:
![]()
![]() +
+![]() .
.
Если в формуле (1) отбросить бесконечно
малые
![]() и
и![]() и заменить полное приращение приближенно
полным дифференциалом, то получим
следующую формулу для приближенного
нахождения значений функции с помощью
полного дифференциала.
и заменить полное приращение приближенно
полным дифференциалом, то получим
следующую формулу для приближенного
нахождения значений функции с помощью
полного дифференциала.
![]()
![]() +
+![]() +
+![]() .
(4)
.
(4)
Пример.Вычислим приближенно число
![]()
Для этого мы вычислим приближенное
значение функции
![]() в точке
в точке![]() ,
где
,
где![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() =
=![]() :
:
![]()
![]() =
=![]() ,
,![]()
![]() ,
,
![]()
![]() ;
;![]()
![]() .
.
Подставив эти значения в (4), получим:
![]() .
.
2. Уравнение касательной плоскости и нормали к поверхности
Определение 1. Касательной плоскостью
к поверхности в её точке
![]() (точка касания) называется плоскость,
содержащая в себе все касательные к
кривым, проведенным на поверхности
через эту точку.
(точка касания) называется плоскость,
содержащая в себе все касательные к
кривым, проведенным на поверхности
через эту точку.
Определение 2. Нормалью к поверхности называется прямая, перпендикулярная к касательной плоскости и проходящая через точку касания.
Пусть функция
![]() имеет в окрестности некоторой точки
имеет в окрестности некоторой точки![]() непрерывные производные
непрерывные производные
Теорема.Через любую точку
![]() функции
функции![]() можно провести касательную плоскость
к ее поверхности.
можно провести касательную плоскость
к ее поверхности.
А) для функции в явном виде
![]() :
:
![]()
Б) для функции в неявном виде
![]() =0:
=0:
![]() .
(2)
.
(2)
Для функции двух переменных
![]() перпендикулярен касательной к линии
уровня этого поля и уравнение этой
касательной по аналогия с (2) можно
записать в виде
перпендикулярен касательной к линии
уровня этого поля и уравнение этой
касательной по аналогия с (2) можно
записать в виде
![]() .
(3)
.
(3)
Тогда уравнение нормали будет:
А) для функции в неявном виде:
![]() (4)
(4)
Б) для функции в явном виде:
![]() (5)
(5)
