
Л-я вышмат 6-7
.docЛекция 6-7
Линейные уравнения с постоянными коэффициентами
Вопросы
1.Линейные однородные дифференциальные уравнения с постоянными коэффициентами. 2.Метод Эйлера. Характеристическое уравнение.
3. Составление частного решения неоднородного линейного дифференциального уравнения с постоянными коэффициентами методом подбора.
Определение1. Если в линейном дифференциальном уравнении, вида:
![]() (1)
(1)
все
![]() - постоянные, то оно называется линейным
уравнением с постоянными коэффициентами.
- постоянные, то оно называется линейным
уравнением с постоянными коэффициентами.
1. Однородные уравнения
Найдем фундаментальную систему уравнения,
правая часть которого равна нулю.
Обозначим его - (2). Частное решение ищем
в виде
![]() ,
где
,
где
![]() - постоянная. Подставляя в (2)
- постоянная. Подставляя в (2)
![]() ,
получим
,
получим
![]() .
.
Так как
![]() то
то
![]() будет решением уравнения (2), если
будет решением уравнения (2), если
![]() будет корнем характеристического
уравнения
будет корнем характеристического
уравнения
![]()
Рассмотрим вопрос отыскания фундаментальной
системы для
![]() .
.
![]() (3)
(3)
Характеристическое уравнение имеет вид
![]() (4)
(4)
Возможны следующие случаи:
1)
![]() .
Тогда
.
Тогда
![]() -
действительные корни (4). Частные решения
-
действительные корни (4). Частные решения
![]() и
и
![]() образуют фундаментальную систему так
как
образуют фундаментальную систему так
как
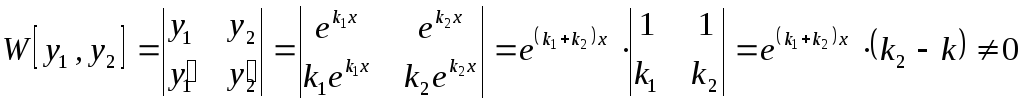 так как
так как
![]()
Общее решение уравнения (3)
![]()
2)
![]() .
Корни комплексные, сопряжённые:
.
Корни комплексные, сопряжённые:
![]() .
Частные решения:
.
Частные решения:
![]() .
.
Из
![]() и
и
![]() .
Следовательно фундаментальная система
.
Следовательно фундаментальная система
![]() а общее решение
а общее решение
![]() .
.
3)
![]() .
Тогда
.
Тогда
![]() .
Получим только одно решение
.
Получим только одно решение
![]() .
Найдем 2-е решение, независимое от
.
Найдем 2-е решение, независимое от
![]() .
Решение ищем в виде
.
Решение ищем в виде
![]() .
.
![]()
Фундаментальная система:
![]() ,
,
![]() .
Общее решение
.
Общее решение
![]()
Следовательно, для решения уравнения (2) необходимо:
1) Составить и решить характеристическое уравнение.
2) Найти фундаментальную систему решений:
а) Каждому однократному действительному
корню
![]() соответствует частное решение
соответствует частное решение
![]() .
.
Б) Каждой паре однократных комплексных
корней
![]() соответствуют два частных решения:
соответствуют два частных решения:
![]()
в) Каждому
![]() -
кратному действительному корню
-
кратному действительному корню
![]() соответствует
соответствует
![]() частных решений:
частных решений:
![]() .
.
Г) Каждой паре
![]() -кратных
корней
-кратных
корней
![]() соответствуют
соответствуют
![]() решений:
решений:
![]()
![]()
Количество частных решений ровно
![]() и они образуют фундаментальную систему.
и они образуют фундаментальную систему.
Записать общее решение
![]() .
.
Пример 1. Найти общее решение уравнений.
А)
![]() .
.
1. Составим и решим характеристическое уравнение
![]() .
.
2.Найдем фундаментальную систему
![]() .
.
![]() -
двукратный корень:
-
двукратный корень:
![]()
![]() .
.
3. Общее решение
![]()
б)
![]()
1.
![]() - двукратный корень.
- двукратный корень.
2.
![]() .
.
3.
![]() .
.
2. Неоднородные уравнения
Для уравнения с постоянными коэффициентами
и специальными правыми частями
![]() частные решения можно найти проще, не
применяя метод вариации.
частные решения можно найти проще, не
применяя метод вариации.
Пусть
![]() и
и
![]() - многочлены
- многочлены
![]() -ой
и
-ой
и
![]() -ой
степени, а
-ой
степени, а
![]() -
кратность корня
-
кратность корня
![]()
![]() характеристического уравнения, причем,
если
характеристического уравнения, причем,
если
![]()
![]() не является корнем, то
не является корнем, то
![]() .
.
Если
-
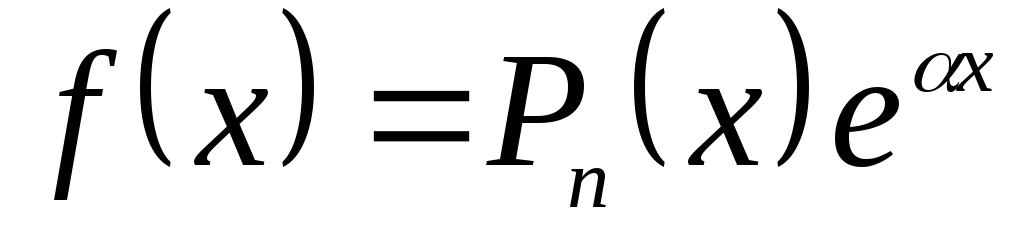 ,
то частное решение ищут в виде
,
то частное решение ищут в виде
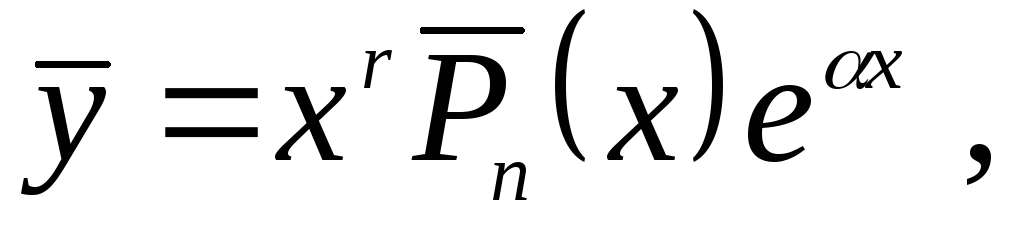 где
где
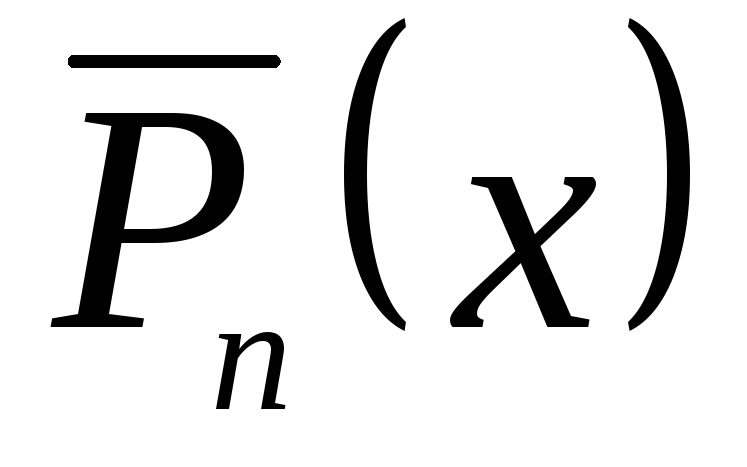 - много-член с неопределенными
коэффициентами.
- много-член с неопределенными
коэффициентами. -
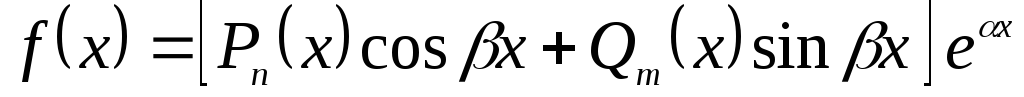 ,
то
,
то
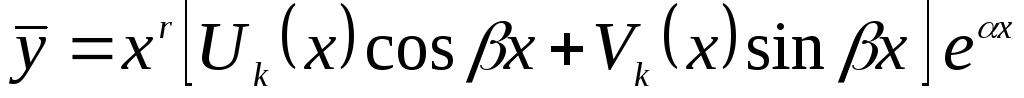 ,
где
,
где
 ,
а
,
а
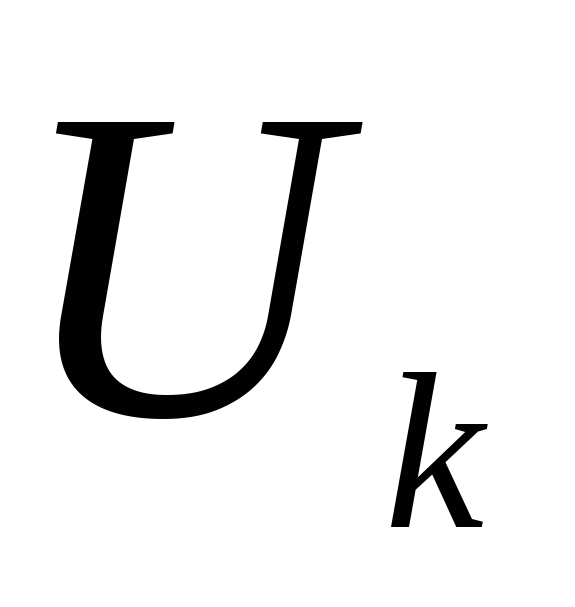 и
и
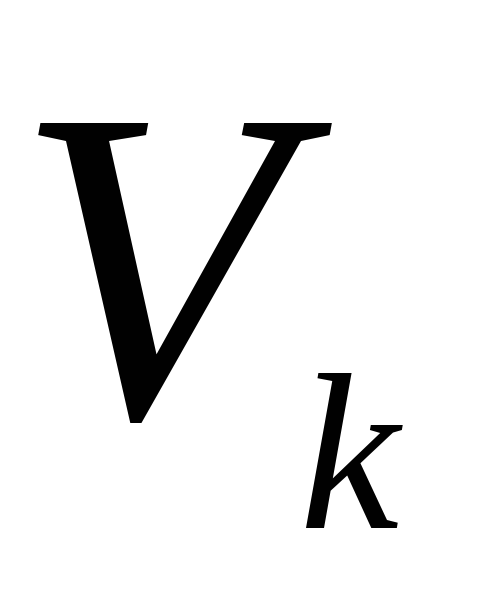 - многочлены с неопределенными
коэффициентами.
- многочлены с неопределенными
коэффициентами.
Пример 3. Найти общее решение уравнений
а)
![]() (8)
(8)
-
Найдем общее решение однородного уравнения
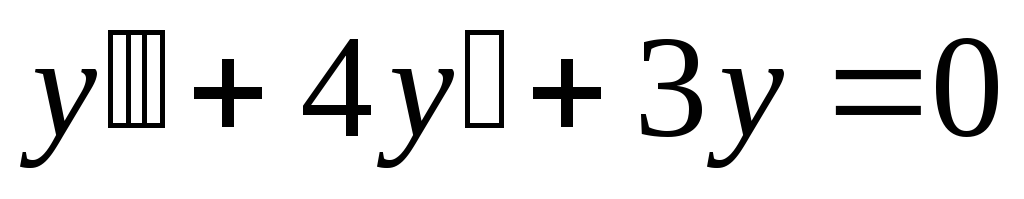 .
. -

-
Найдем частное решение уравнения (8):
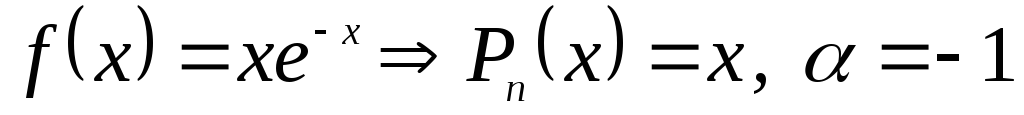 - однократный корень
- однократный корень
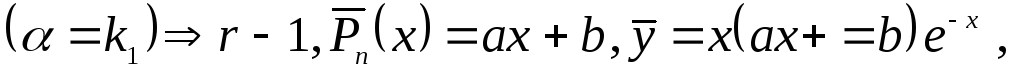 где
где
 и
и
 надо подобрать так, чтобы
надо подобрать так, чтобы
 был решением (8).
был решением (8).
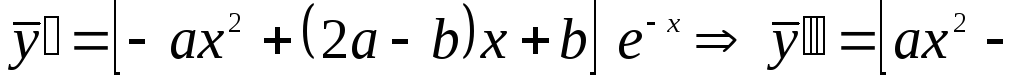
![]() .
.
Подставляя
![]() ,
,
![]() ,
,
![]() в (8) и приравнивая коэффициенты у
одинаковых степеней
в (8) и приравнивая коэффициенты у
одинаковых степеней
![]() ,
получим
,
получим
![]()
![]()
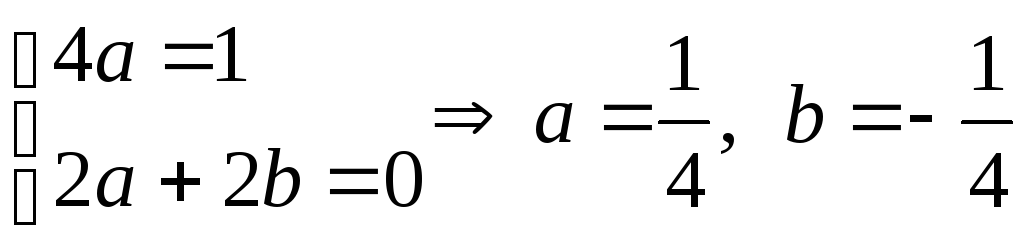 .
.
Частное решение
![]() ,
а общее -
,
а общее -
![]() .
.
б)
![]() .
.
![]() -
общее решение однородного уравнения.
-
общее решение однородного уравнения.
-
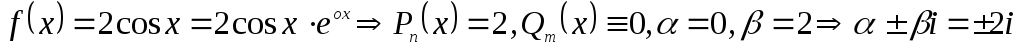 не корнем
не корнем
![]()
![]() .
Подставляя
.
Подставляя
![]() ,
,
![]() ,
,
![]() в уравнение, получим.
в уравнение, получим.
![]()
 .
.
Общее решение
![]() .
.
Пример из экономики. Модель Самуэльсона – Хикса.
Решение уравнений, вида
![]() ,
,
где
![]() - члены некоторой числовой последовательности,
- члены некоторой числовой последовательности,
![]() -
постоянные числа,
-
постоянные числа,
![]() -
некоторая функция натурального числа,
называется линейным разностным
уравнением
-
некоторая функция натурального числа,
называется линейным разностным
уравнением
![]() -ого
порядка.
-ого
порядка.
Методы решения данного уравнения, широко используемого в экономике, аналогичны решению ЛДУ с постоянными коэффициентами.
Продемонстрируем это для разностных уравнений 2-ого порядка, вида:
![]() .
.
Так же как и для ЛДУ, общее решение данного уравнения определяется по формуле:
![]() ,
,
где
![]() -
некоторое частное решение данного
уравнения, а
-
некоторое частное решение данного
уравнения, а
![]() - общее решение соответствующего
однородного уравнения. Для нахождения
последнего решения необходимо найти
корни характеристического уравнения
- общее решение соответствующего
однородного уравнения. Для нахождения
последнего решения необходимо найти
корни характеристического уравнения
![]() .
.
Могут возникнуть три варианта.
-
Оба корня действительные и различные, тогда
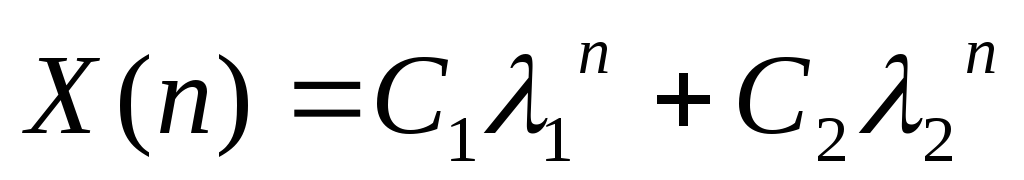 .
. -
Оба корня действительные и равные
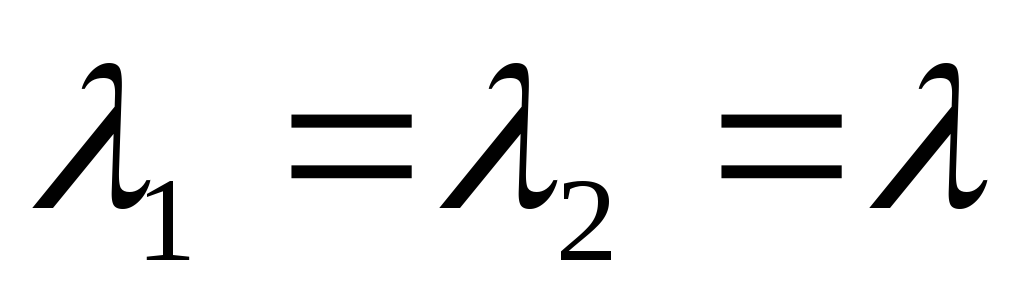 ,
тогда
,
тогда
 .
. -
Корни комплексно-сопряженные, тригонометрическая форма, вида
 ,
тогда
,
тогда
 .
.
Пример 4. Решить уравнение
![]() .
.
Решение. Методом неопределенных
коэффициентов найдем частное решение
в виде:
![]() .
Подставляя это выражение в уравнение,
получим
.
Подставляя это выражение в уравнение,
получим
![]() .
.
Следовательно,
![]() и
и
![]() .
.
Решая характеристическое уравнение:
![]() находим
находим
![]() .
Таким образом, общее решение уравнения
имеет вид:
.
Таким образом, общее решение уравнения
имеет вид:
![]() .
.
Рассмотрим уравнение Хикса:
![]() .
.
Частное решение данного уравнения найдем из условия
![]() ,
,
Это так называемое равновесное решение.
Подставляя его в данное уравнение,
получаем
![]() ,
откуда получаем
,
откуда получаем
![]() .
Заметим, что множитель
.
Заметим, что множитель
![]()
![]() называется
мультипликатором Кейнса и является
одномерным аналогом матрицы полных
затрат.
называется
мультипликатором Кейнса и является
одномерным аналогом матрицы полных
затрат.
В этих терминах рассмотрим модель
Самуэльсона – Хикса при условии:
![]() В этом случае уравнение примет вид:
В этом случае уравнение примет вид:
![]()
Его частным решением будет функция
![]() найдем корни характеристического
уравнения
найдем корни характеристического
уравнения
![]() Имеем
Имеем
![]()
Таким образом, общим решением искомого уравнения будет
![]()
В зависимости от
![]() возможны четыре типа динамики. Она может
быть растущей или затухающей и при этом
иметь или не иметь колебательный
характер.
возможны четыре типа динамики. Она может
быть растущей или затухающей и при этом
иметь или не иметь колебательный
характер.
Литература
-
Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. М.: Наука, 1985г.
-
Краснов М.Л. Обыкновенные дифференциальные уравнения. М.: Высшая школа 1983г.
-
Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т.1,2 М.: Наука, 1985г.
-
Сборник индивидуальных заданий по высшей математике ч.1-3 Под редакцией Рябушко А.П. Минск.: Вышейшая школа, 2001 г.
-
Данко П.Е., Попов А.Г., Кожевников Т.Я. Высшая математика в упражнениях и задачах. Ч.1,2 М.: Высшая школа,1986 г.
-
Кузнецов Л.А. Сборник заданий по высшей математике (типовые расчеты). М.: Высшая школа, 1983 г.
