Лекция 14 Случайные величины и их числовые характеристики. Числовые характеристики случайной величины. Распределения непрерывных случайных величин. Закон больших чисел. Вопросы

1. Случайная дискретная величина .

2.Закон распределения случайно величины.

3. Непрерывная случайная величина.

4. Интегральной функции и ее свойства.

5. Дифференциальная функция и ее свойства.

6.Математическое ожидание для дискретной случайной величины.

7.Вероятностный смысл математического ожидания.

8.Свойства мат. ожидания.

9.Отклонение.

10.Дисперсия случайной дискретной величины и ее свойства.

11.Вероятностный смысл дисперсии.

12.Свойства дисперсии.

13.Закон равномерного распределения.

14.Нормальное распределение. Нормальная кривая.

1. Дискретные и непрерывные случайные величины

Определения.

1. Случайной величиной называется величина, которая в результате опыта может принять то или иное (но только одно) значение, причем заранее до опыта неизвестное.

2. Величина, принимающая отдельные изолированные возможные значения, называется

дискретной.

Например:

а) Х – число нестандартных деталей в партии из штук. Х может принимать значения:.

б) Х – число выстрелов до первого попадания в цель .

3. Непрерывной случайной величиной называется величина, возможные значения которой, заполняют сплошь некоторый интервал.

Например.Х – расстояние, которое пролетит снаряд при выстреле из орудия:.

2. Закон распределения дискретных случайных величин

Для полного определения случайной величины Х, кроме возможных значений Х, необходимо указать связь между возможными значениями и соответствующими вероятностями. Эта связь называется законом распределения Х и для дискретной случайной величины ее можно задать в виде ряда распределения

			…
			…

где .

Можно задать также графически в виде многоугольника распределений.

3. Распределение непрерывных случайных величин

Закон распределения нельзя строить для непрерывной случайной величины. Поэтому наиболее общей формой закона распределения величины Х является функция распределения (интегральная функция). .

Для дискретной величины Х , а для непрерывной – вероятность того, что случайная точка Х в результате опыта попадает левее точки.

Свойства .

1.

2.

3. - неубывающая функция

4.

В дальнейшем величину Х считаем непрерывной, если - непрерывна.

Более наглядное представление, чем , о характере распределения непрерывной величины Х в окрестностях различных точек дается функцией плотности распределения (дифференциальной функцией).

Свойства

1.

2.

3.

4.

Пример 1.Построить графики, если

Решение.

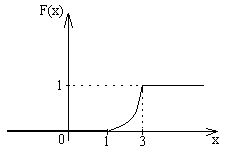
Найдем

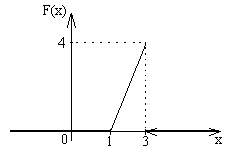
4. Числовые характеристики случайной величины

Числовые характеристики выражают наиболее существенные особенности данного распределения.

Определение.Математическим ожиданием случайной величины Х называется

а) Х – дискретная величина

б) Х – непрерывная величина

Математическое ожидание можно рассматривать как центр рассеивания величины Х. Если проводится опытов, топриближенно равна среднему арифметическому наблюдаемых значений Х.

Основными характеристиками рассеивания Х около являютсяи среднее квадратическое отклонение, где:

а) Х – дискретная

Кроме указанных числовых характеристик используются и другие: мода, медиана, моменты и др.

Начальные и центральные теоретические моменты.

Определение.Начальным моментом порядка к случайной величины Х называют маматическое ожидание величины Х^к:

Аналогично для дисперсии

Определение.Центральным моментом порядка к сл.вел. Х называют математическое ожидание и величины:

Легко выводятся связь между и

Пример 2. Дано

X	0,1	2	10	20
p	0,4	0,2	0,15	0,25

Экономический пример 3. Компания продает некоторый продукт, учет продаж которого ведется в тысячах штук. Закон распределения объема ежемесячных продаж продукта представлен в таблице. Найдем ожидаемое среднее значение числа месячных продаж.

Число единиц товара х, тыс, шт.	Р(х)
5000 6000 7000 8000 9000	0,2 0,3 0,2 0,2 0,1
	1,0

Решение. Из формулы (3.4) следует, что М(Х) = 5000∙0,2 + 6000∙0,3+ + 7000∙ 0,2 + 8000∙ 0,2 + 9000∙ 0,1 = 1000 + 1800 + 1400 + + 1600 + 900 = 6700.

Пример 4. Каждый день местная газета получает заказы на новые рекламные объявления, которые будут напечатаны в завтрашнем номере. Число рекламных объявлений в газете зависит от многих факторов: дня недели, сезона, общего состояния экономики, активности местного бизнеса и т. д. Пусть X – число новых рекламных объявлений, напечатанных в местной газете в определенный день. X – случайная величина, которая может быть только целым числом. В нашем примере случайная величина X принимает значения 0; 1; 2; 3; 4; 5 с вероятностями 0,1; 0,2; 0,3; 0,2; 0,1; 0,1 соответственно. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины X – числа рекламных объявлений в газете в заданный день.

Решение. Ряд распределения случайной величины X

xi	0	1	2	3	4	5
P(xi)= pi	0,1	0,2	0,3	0,2	0,1	0,1

Вычисление математического ожидания числа рекламных объявлений:

хi	0	1	2	3	4	5	n
P(хi)	0,1	0,2	0,3	0,2	0,1	0,1
хiP(хi)	0,0	0,2	0,6	0,6	0,4	0,5	М(Х) = 2,3

Можно сказать, что в среднем 2,3 рекламных объявления ежедневно помещаются в газете. Это – ожидаемое среднее число рекламных объявлений в заданный день. Дисперсия вычисляется так:

σ² = [x_i–M(X)]²P(x_i) = (0–2,3)² + (1–2,3)² + (2–2,3)² + (3–2,3)² + (4–2,3)² + (5 – 2,3)² = 2,01. Среднеквадратическое отклонение