1.8 Кездейсоқ шамалардың сандық сипаттамалары

Х кездейсоқ шамасының математикалық күтімі деп

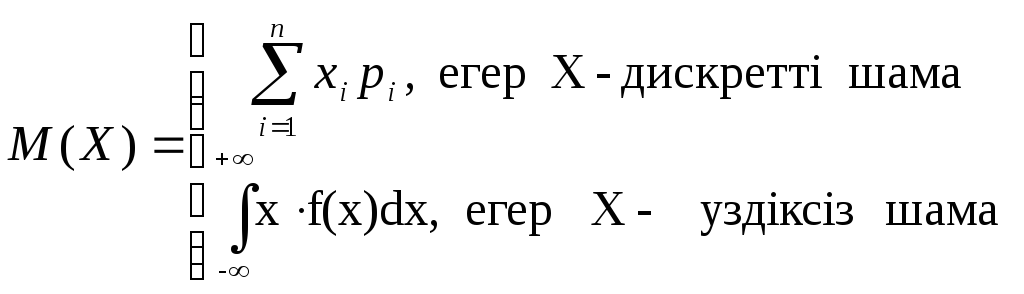
формуласымен анықталатын шаманы айтамыз. Математикалық күтімнің төмендегідей қасиеттері бар:

1. M(C)=C;

2. M(CX)=C M(X);

3. M(X+Y)=M(X)+M(Y),

бұл формулалардағы С - тұрақты шама; X,Y – кездейсоқ шамалар.

Х кездейсоқ шамасының дисперсиясы деп

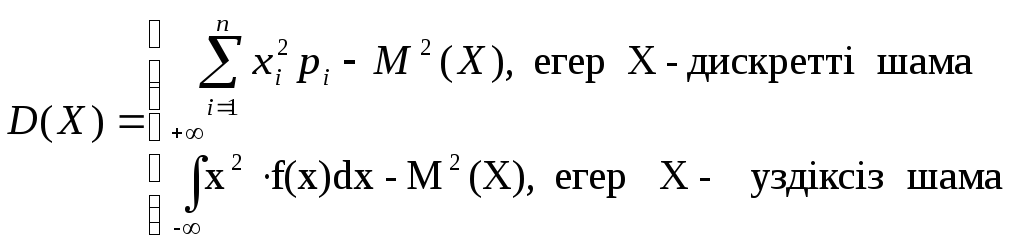
формуласымен анықталатын шаманы айтамыз. Дисперсияның төмендегідей қасиеттері бар:

1.D(C)=0;

2. D(CX)=C² D(X);

3. D(X+Y)=D(X)+D(Y);

4. D(X)³0,

бұл формулалардағы С - тұрақты шама; X,Y – кездейсоқ шамалар.

Орта квадраттық ауытқу деп:

s=

формуласы бойынша есептелінетін шаманы айтамыз.

Кездейсоқ шаманың моменттері:

Х кездейсоқ шамасының k ретті алғашқы моменті n_k деп

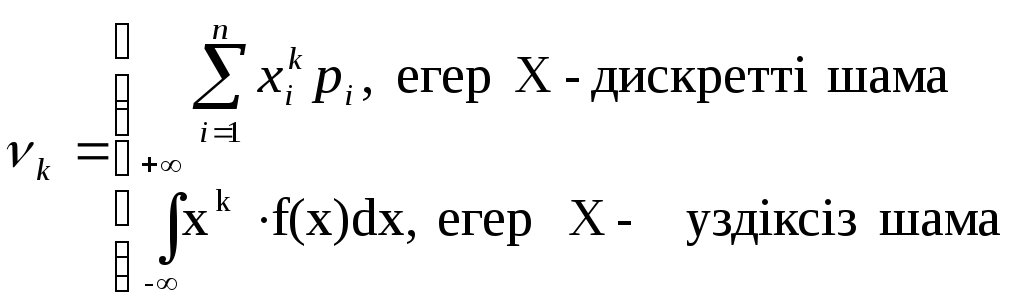
формуласымен анықталатын шаманы айтамыз.

Х кездейсоқ шамасының k-шы ретті орталық моменті m_k деп:

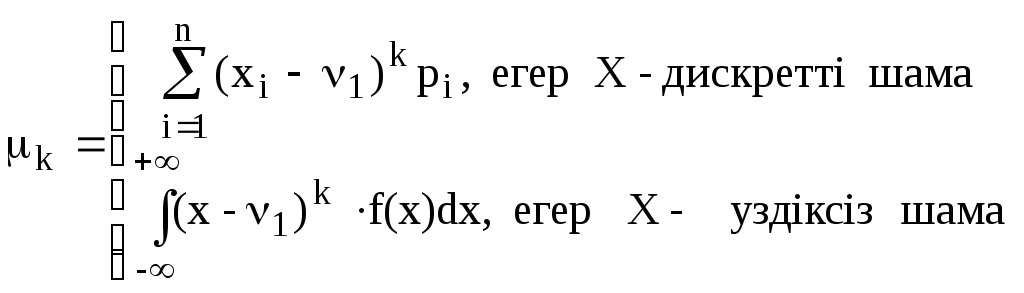
формуласымен анықталатын шаманы айтамыз.

Алғашқы және орталық момент арасында мынадай байланыс бар:

m₂ = n₂ - n₁²;

m₃=n₃ - 3n₁ n₂+2n₁³;

m₄=n₄-4n₃n₁+6n₂n₁²-3n₁⁴.

Үлестірім заңдылығының асимметриясы мен эксцессі:

Үлестірім заңдылығының асимметриясын арқылы белгілейміз:

Үлестірім заңдылығының эксцессін арқылы белгілейміз:

2 Есептеу тапсырмаларын орындау үлгісі

2.1 Геометриялық ықтималдық

2.1.1- мысал : Радиустары 6 см және 4 см болатын концентрлі екі шеңбер берілген. Егер нүктенің шеңберге түсу ықтималдығы шеңбер ауданына пропорционал болса және орналасуына байланысты емес болса, онда үлкен дөңгелекке лақтырылған нүктенің үлкен және кіші дөңгелек арасында пайда болған сақинаға түсу ықтималдығын табыңыз.

Шешуі: А оқиғасы – «үлкен дөңгелекке лақтырылған нүктенің сақинаға түсуі». Лақтырылған нүкте үлкен дөңгелекке түсуі мүмкін, барлық сынақтар жиыны үлкен дөңгелек ауданы: 36pR². Ал сақинаның ауданы 36pR² -16pR² =20pR² . Яғни, бұл А оқиғасын қанағатттандыратын сынақтар жиыны. Ендеше, р(А)=.

Жауабы:

2.1.2 - мысал: Екі оқиғаның кездейсоқ басталу уақыты 11⁰⁰ – сағаттан 13⁰⁰ сағатқа дейін.

Оқиғаның біреуі 10 минутқа, екіншісі 15 минутқа созылады.

а) оқиғалардың уақытпен қиылысу ықтималдығын;

б) оқиғалардың уақытпен қиылыспау ықтималдығын табу керек.

Шешуі: у 10 х 15 120

А- оқиғалардың уақытпен қиылысуы; Оқиғалардың басталу моментін сәйкесінше x және y деп белгілейік. x пен y тің мүмкін мәндер жиыны - келесі теңсіздіктермен анықталады: 11 –ді уақыттың басталуы деп қабылдағанбыз, уақыт минутпен есептеледі. Ендеше x пен y тің қиылысуының мәндер жиыны келесі теңсіздіктермен анықталады:

;

Әрбір x ;y мәндер жұбына тік бұрышты координаталар жүйесінің жазықтығындағы (x ;y) нүктесі сәйкестендірейік.

Ендеше жиынына қабырғасы 120 болатын квадрат сәйкес келеді, алжиынына:

түзулері арасындағы квадраттың жолағы сәйкес келеді. Сөйтіп, А оқиғасының ықтималдығы:

а) геометриялық ықтималдықтың анықтамасы бойынша:

түрінде табылады.

б) В-оқиғалардың уақытпен қиылыспауы;

Бұл А оқиғасына қарама қарсы оқиға, ендеше оқиғаның орындалу ықтималдығы келесі түрде табылады:

Жауабы:;