shpory

9. y функциясының туындысының берілген нүктедегі мәнін анықтаңыз:

y=ln(1 – 2x) y^/(1)=?

В) 2

10. y функциясының туындысының берілген нүктедегі мәнін анықтаңыз:

y=arcSin2x y^/(0)=?

С) 2

11. Лопиталь ережесінің көмегімен шегін табу керек:

A) 2

12. , егер функция x=sin²t, y=cos²t болса.

D) -1

13. Лопиталь ережесінің көмегімен шегін табу керек:

D) 2

14. Лопиталь ережесінің көмегімен шегін табу керек:

E) 0

15. Лопиталь ережесінің көмегімен шегін табу керек:

D)

16. y функциясының туындысының берілген нүктедегі мәнін анықтаңыз:

y= y^/(0)=?

E) 0

17. y функциясының туындысының берілген нүктедегі мәнін анықтаңыз:

y= y^/(0)=?

B) -

18. y функциясының туындысының берілген нүктедегі мәнін анықтаңыз:

y= y^/(0)=?

A)

19. y функциясының туындысының берілген нүктедегі мәнін анықтаңыз:

y= y^/(0)=?

E) 0

20. y функциясының туындысының берілген нүктедегі мәнін анықтаңыз:

y= y^/(0)=?

B) 1

21. y функциясының туындысының берілген нүктедегі мәнін анықтаңыз:

y= y^/(0)=?

B) 1

22. y= функциясының екінші ретті туындысын х=0 нүктесінде есептеңіз:

C) -2

23. = функциясының екінші ретті туындысын х=0 нүктесінде есептеңіз:

B) 6

24. Лопиталь ережесінің көмегімен шегін табу керек:

B) -1

25. Лопиталь ережесінің көмегімен шегін табу керек:

B) 1

13. Монотондылық аралықтары, стационар нүктелері және экстремумдары.

Ойыс, дөңес аралықтар. Иілу нүктесі.

1. у=х²+1 функциясының кему аралықтарын табыңыз

D) (-¥ 0)

2. у=х²+1 функциясының өсу аралықтарын табыңыз.

D) (0+¥)

3. функциясының кему аралықтарын табыңыз

А) (01) (1е)

4. функциясының өсу аралықтарын табыңыз

В) (е+¥)

5. у=х³+х функциясының өсу аралықтарын табу керек.

С) (-¥ +¥)

6. у=х²-1 функциясының экстремумдарын табу керек.

А) y_min(0)=-1

7. у=х² +1 функциясының экстремумдарын табу керек.

D) y_min(0)=1

8. функциясын экстремумға зертте

В) Экстремум нүктелері жоқ

9. функциясын экстремумға зертте

С) Экстремум нүктелері жоқ

10. у = х² + 2х + 1 функциясын экстремумдарға зертте

А) y_min(-1)=0

11.y=x³-3x²+5x+1 функциясының иілу нүктесінің координаталарын табыңыз

B) (14)

12.y=-x²+4x функциясының кризистік нүктелерін тап:

C) x=2

13.y=xe^-x функциясының кризистік нүктелерін тап:

A) x=1

14. y= функциясының экстремум нүктелерін тап:

C) max=, min=

15. =-4x³+12x+5 функциясының өсу аралығын табыңыз:

B)

16.=2x³-6x+5 функциясының иілу нүктесін табыңыз:

E) x=0

17. y=-x+12x функциясының экстремум нүктелерін тап:

A) max=2, min=-2

18. =3x-9x+5 функциясының кемімелі аралығын табыңыз:

B)

19.=2x³-6x+5 функциясының кемімелі аралығын табыңыз:

B)

20=4x-12x+3 функциясының өспелі аралығын табыңыз:

A)

21. функциясын экстремумға зертте

В) Экстремум нүктелері жоқ

22. функциясын экстремумға зертте

С) Экстремум нүктелері жоқ

23.y=x³-3x² функциясының өсу аралығын табыңыз

A)

E) функция монотонды кемімелі

24. =2x³-6x функциясының кемімелі аралығын табыңыз:

B) C)

25.y=2x 3x² функциясын экстремумға зертте:

A) max=0, min=-1

14. Бір айнымалыға байланысты функцияның туындысы.

1. у =¦(х) дифференциалданатын функциясының М(х₀у₀) нүктесіндегі жанамасының теңдеуі:

С)

2. у =¦(х) дифференциалданатын функциясының М(х₀у₀) нүктесіндегі нормалінің теңдеуі:

В)

3. функциясының туындысы: В)

4. функциясының туындысы:

А)

5. у =¦(х) функциясының логарифмдік туындысы:

А)

6. у=кх + в түзуі у =¦(х) функциясының көлбеу асимптотасы болса, онда к шамасын төмендегі теңдіктен анықтаймыз:

В) немесе

7. у=кх + в түзуі у =¦(х) функциясының көлбеу асимптотасы болса, онда в шамасын төмендегі теңдіктен анықтаймыз:

Е) немесе

8. параметрге байланысты функциясының 1-ретті туындысын анықтайтын

формуланы көрсетіңіз:

А)

9. х = түзуі у =¦(х) функциясының вертикаль асимтотасы болса, онда:

С) 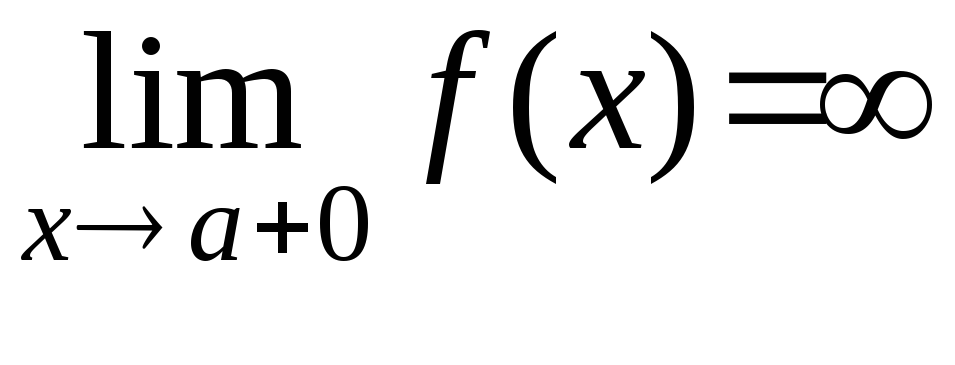немесе

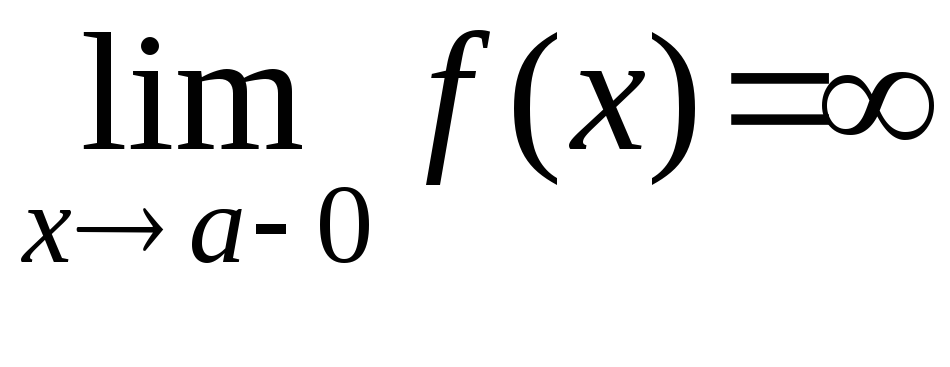
10 функциясының нүктесіндегі туындысы деп төмендегі шектің нақты мәнін айтамыз:

C)

11. у =¦(х) қисығы берілген аралықта ойыс болуы үшін, сол аралықта қандай болуы керек?

А) ¦^// (х)> 0

12. у =¦(х) қисығы берілген аралықта дөңес болуы үшін, сол аралықта қандай болуы керек ?

А) ¦^// (х)< 0

13. у =¦(х) функциясына х₀ нүктесі иілу нүктесі болуы үшін қажетті шарт:

В) ¦^// (х₀)= 0

14. у =¦(х) функциясына х₀ нүктесі иілу нүктесі болуы үшін жеткілікті шарт:

Осы нүктеден өткенде:

А) ¦^// (х) – таңбасы өзгереді

15. х₀ нүктесі у =¦(х) функциясының иілу нүктесі деп аталады, егер осы нүктеде:

С) Қисық ойыстықтан дөңестіккке ауысса (немесе керісінше)

16. ¦^/ (х₁)= 0 болсын, онда х =х₁ нүктесінде функцияның максимумы болуы үшін:

А) ¦^// (х₁)< 0

17. ¦^/ (х₁)= 0 болсын, онда х =х₁ нүктесінде функцияның минимумы болуы үшін:

Е) ¦^// (х₁)> 0 болуы жеткілікті

18. ¦^/ (х₁)= 0 және ¦^// (х₁)< 0 болсын , онда х₁ нүктесі ¦(х) функциясы үшін:

А) максимум нүктесі

19. ¦^/ (х₁)= 0 және ¦^// (х₁)> 0 болсын, онда х₁ нүктесі ¦(х) функциясы үшін:

С) минимум нүктесі

20. Төмендегі ұйғарымдардың қайсысы дұрыс:

А) Егер функция дифференциалданатын болса, онда үзіліссіз

21. Коши теоремасы. Егер функцияларысегментінде үздіксіз, (а,в) интервалында дифференциалданатын және болса, онда осы аралықтан нүктесі табылып, келесі теңдік орындалады.

А)

22. Лагранж теоремасы: сегментінде үздіксіз және (а,в) интервалында дифференциалданатын f(x) функциясы үшін осы интервалдан бір нүктесі табылып, келесі теңдік орындалады.

В)

23. Лопиталь теоремасының шарттары орындалса, онда:

С)

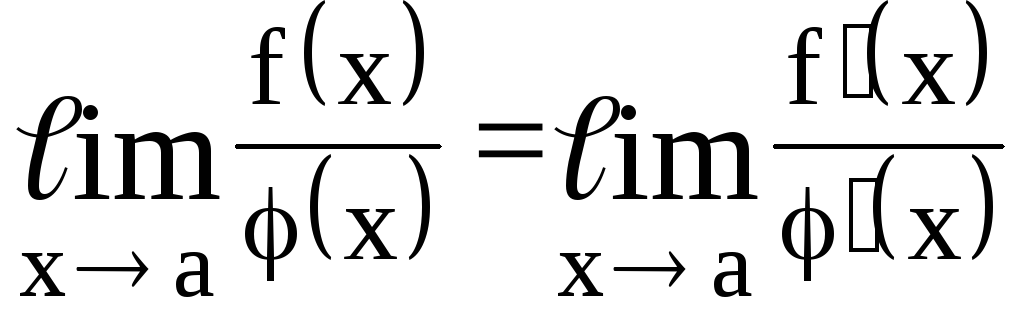
24. Лопиталь ережесін қолдану үшін анықталмағандық түрі қандай болуы керек?

В)

25. Ролль теоремасы. сегментінде үздіксіз, (а,в) интервалында дифференциалданатын және f(a)=f(b) шарты орындалатын f(x) функциясы үшін осы интервалда нүктесі табылып, келесі теңдік орындалады.

B) f^/(с)=0

15. Қарапайым интегралды табу.

1. - интегралын табыңыз:

B)

2. - интегралын табыңыз:

E)

3. - интегралын табыңыз:

D) ln|y+ | +C

4. - интегралын табыңыз:

D) ln|у -5|+C

5. - интегралын табыңыз:

A) x-arctgx+C

6. - интегралын табыңыз:

C)

7. - интегралын табыңыз:

D)

8. - интегралын табыңыз:

A)

9. - интегралын табыңыз:

A) x-ln|x|+C

10. - интегралын табыңыз:

D)

11. - - интегралын табыңыз:

A)

_12.

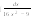- интегралын табыңыз:

А)

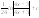
_13.

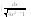- интегралын табыңыз:

Е)

14. - интегралын табыңыз:

D)

15. - интегралын табыңыз:

B)

16. - интегралын табыңыз:

С)

17. - интегралын табыңыз:

D)

18. - интегралын табыңыз:

B)

19. - интегралын табыңыз:

С)

20. - интегралын табыңыз:

А)

21. - интегралын табыңыз:

В) 2

22. - интегралын табыңыз:

А)

23. - интегралын табыңыз:

D)

24. - интегралын табыңыз:

А)

25. - интегралын табыңыз:

Е)

16. Айнымалыны ауыстыру әдісі бойынша интегралды есептеу.

1. - интегралын айнымалыны ауыстыру әдісімен табу керек:

В)

2. - интегралын айнымалыны ауыстыру әдісімен табу керек:

Е)

3. - интегралын айнымалыны ауыстыру әдісімен табу керек:

В)

4. - интегралын айнымалыны ауыстыру әдісімен табу керек:

А)

5. - интегралын айнымалыны ауыстыру әдісімен табу керек:

D)

6. - интегралын айнымалыны ауыстыру әдісімен табу керек:

D)

7. - интегралын айнымалыны ауыстыру әдісімен табу керек:

С)

8. - интегралын айнымалыны ауыстыру әдісімен табу керек:

A) ln|3у -2|+C

9. - интегралын айнымалыны ауыстыру әдісімен табу керек:

Е)

10. - интегралын айнымалыны ауыстыру әдісімен табу керек:

С)

11. - интегралын айнымалыны ауыстыру әдісімен табу керек:

D) –2+c

12. - интегралын табыңыз:

B)

13. - интегралын айнымалыны ауыстыру әдісімен табу керек:

В)

14. - интегралын айнымалыны ауыстыру әдісімен табу керек:

Е)

15. - интегралын айнымалыны ауыстыру әдісімен табу керек:

В)

16. - интегралын айнымалыны ауыстыру әдісімен табу керек:

А)

17. - интегралын айнымалыны ауыстыру әдісімен табу керек:

D)

18. - интегралын айнымалыны ауыстыру әдісімен табу керек:

D)

19. - интегралын айнымалыны ауыстыру әдісімен табу керек:

С)

20. - интегралын айнымалыны ауыстыру әдісімен табу керек:

A) ln|17у -15|+C

21. - интегралын айнымалыны ауыстыру әдісімен табу керек:

Е)

22. - интегралын айнымалыны ауыстыру әдісімен табу керек:

С)

23. - интегралын айнымалыны ауыстыру әдісімен табу керек:

D) -+c

24. - интегралын табыңыз:

B)

25. - интегралын айнымалыны ауыстыру әдісімен табу керек:

Е)

17. Бөліктеп интегралдау әдісі бойынша интегралды есептеу.

1. - интегралын бөліктеп интегралдау әдісімен табу керек:

С)

2. - интегралын бөліктеп интегралдау әдісімен табу керек:

В)

3. - интегралын бөліктеп интегралдау әдісімен табу керек:

D)

4. - интегралын бөліктеп интегралдау әдісімен табу керек:

С)

5. - интегралын бөліктеп интегралдау әдісімен табу керек:

А)

6. - интегралын бөліктеп интегралдау әдісімен табу керек:

А)

7. - интегралын бөліктеп интегралдау әдісімен табу керек:

В)

8. - интегралын бөліктеп интегралдау әдісімен табу керек:

В)

9. - интегралын бөліктеп интегралдау әдісімен табу керек:

E)

10. - интегралын бөліктеп интегралдау әдісімен табу керек:

С)

11. - интегралын бөліктеп интегралдау әдісімен табу керек:

А)

12. - интегралын бөліктеп интегралдау әдісімен табу керек:

D)

13. - интегралын бөліктеп интегралдау әдісімен табу керек:

С)

14. - интегралын бөліктеп интегралдау әдісімен табу керек:

В)

15. - интегралын бөліктеп интегралдау әдісімен табу керек:

D)

16. - интегралын бөліктеп интегралдау әдісімен табу керек:

С)

17. - интегралын бөліктеп интегралдау әдісімен табу керек:

А)

18. - интегралын бөліктеп интегралдау әдісімен табу керек:

А)

19. - интегралын бөліктеп интегралдау әдісімен табу керек:

В)

20. - интегралын бөліктеп интегралдау әдісімен табу керек:

В)

21. - интегралын бөліктеп интегралдау әдісімен табу керек:

E)

22. - интегралын бөліктеп интегралдау әдісімен табу керек:

С)

23. - интегралын бөліктеп интегралдау әдісімен табу керек:

А)

24. - интегралын бөліктеп интегралдау әдісімен табу керек:

D)

25. - интегралын бөліктеп интегралдау әдісімен табу керек:

D)

18. Анықталмаған және анықталған интеграл (теориялық сұрақтар)

1. функциясы үшін интегралдық қосындының дұрыс жазылуын көрсет:

E)

2. теңдеуімен берілген қисықтың аралығындағы доғасының ұзындығын есептеу формуласын көрсетініңіз:

С)

3. қисығымен ОХ осімен және түзулерімен шектелген фигураны ОХ осінен айналдырғанда пайда болған фигураның көлемі неге тең:

E)

4. Анықталмаған интегралдарда бөліктеп интегралдау формуласының дұрыс жазылуын көрсет:

C)

5. Анықталған интегралдарда бөліктеп интегралдау формуласының дұрыс жазылуын көрсет:

D)

6. интегралы неге тең: