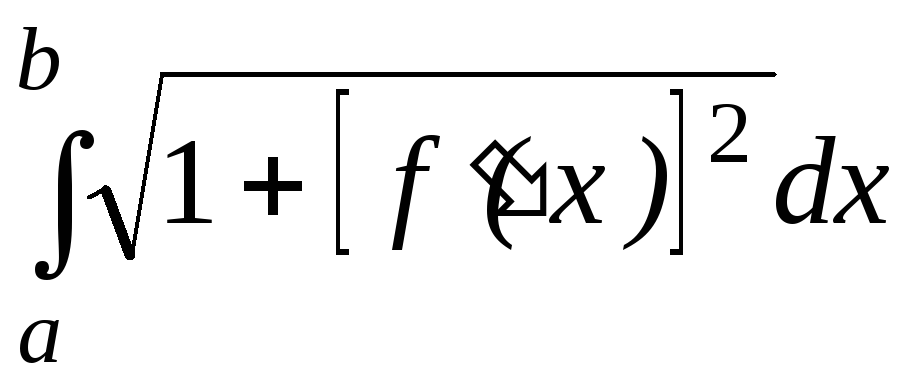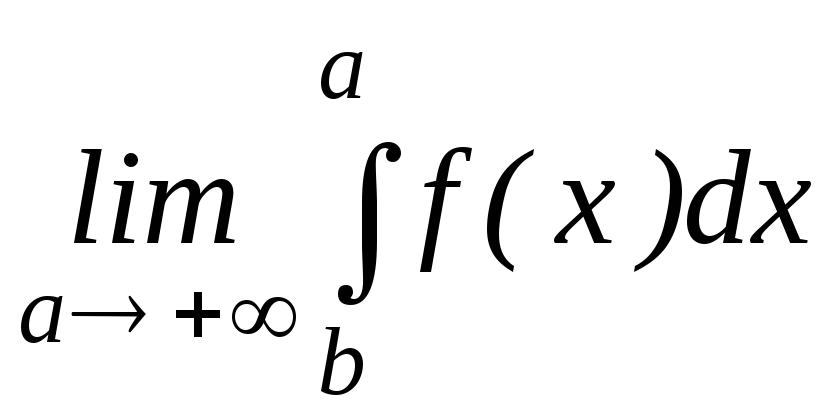Раздел 20

1. Функция называется первообразной функциина промежутке, если функциядифференцируема наи выполняется равенство:

1. 

2. 

3. 

4. 

5. 

2. Укажите целесообразную подстановку для нахождения интеграла .

1. 

2. 

3. 

4. 

5. 

3.

1. 

2. 1

3. 0

4. 

5. 

4. Если –постоянная, то

1. 

2. 

3. 

4. 

5. 

5.

1. 

2. 

3. 

4. 

5. 

6. Если идифференцируемые функции, то

1. 

2. 

3. 

4. 

5. 

7. Для вычисления интеграла вида производится подстановка :

1. 

2. 

3. 

4. 

5. 

8. Интеграл вида приводится к интегралу рациональной дроби с помощью подстановки:

1. 

2. 

3. 

4. 

5. 

9. Определенный интеграл на отрезкеопределяется через предел следующего вида:

1. 

2. 

3. 

4. 

5. 

10. Если интегрируема на и выполнено , то:

1. 

2. 

3. 

4. 

5. 

11. Если непрерывная нафункция инекоторая ее первообразная, то

1. 

2. 

3. 

4. 

5. 

12. Если функция четная, то

1. 

2. 0

3. 1

4. 

5. 

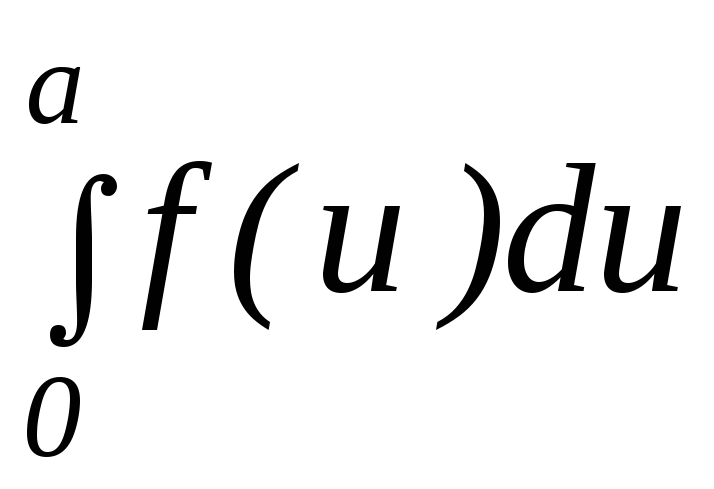
13. Если функция нечетная ,то

1. 

2. 0

3. 1

4. 

5. 

14. Укажите определение несобственного интеграла I-рода

1. 

2. 

3. 

4. 

5. 

15. Чтобы несобственные интегралы ,с единственной особенностью в точкесходились одновременно или расходились оба одновременно, достаточно выполнение следующего условия:

1. 

2. 

3. 

4. 

5. 

16. Если функции в параметрических уравнениях кривойи непрерывны на, то длины дуги

1. 

2. 

3. 

4. 

5. 

17. Если кривая задана уравнением :, то длины дуги

1. 

2. 

3. 

4. 

5. 

18. Если кривая задана с помощью полярных координат : , , то длины дуги

19. Если знак функции меняется наконечное число раз, то площадь плоской фигуры, ограниченной линиямиравна

1. 

2. 

3. 

4. 

5. 

20. Непрерывная на функция на этом отрезке:

1. не интегрируется

2. интегрируется

3. постоянна

4. монотонна

5. непрерывна

21. Чтобы функция была интегрируемой на отрезке, она на этом отрезке:

1. должна быть ограниченной

2. необходимо и достаточно ее ограниченность

3. достаточно, ее неограниченность

4. необходимо, чтобы она была постоянной

5. чтобы она была равна нулю

22. Если интегрируема наивыполнено, то:

1. 

2. 

3. 

4. 

5. 

23. Укажите определение несобственного интеграла I-рода .

1. 

2. 

3. 

4. 

5. 

24. Укажите определение несобственного интеграла 2-рода при:

1. 

2. 

3. 

4. 

5. 

25. Укажите определение несобственного интеграла 2-го рода при

1. 

2. 

3. 

4. 

5. 

26. Если непрерывная нафункция и F(u) некоторая ее первообразная, то

1. 

2. 

3. 

4. 

5. 

27. Если функция дважды дифференцируема на и на этом интервале, то функция на

1. выпуклая вниз(вогнутая)

2. выпуклая вверх(выпуклая)

3. возрастает

4. убывает

5. постоянна

28. Точка , в которой выпуклая часть графика функция сменяется вогнутой (или наоборот), называется точкой

1. перегиба

2. минимума

3. максимума

4. пересечения с осью

5. изменения знака функции

29. Если функция какая-либо первообразная для функции , то выражение называется

1. неопределенным интегралом от функции

2. сопряженной функцией для

3. сложной функцией

4. противоположной функцией для

5. симметричной функцией для

30. Если точка перегиба функция , то в этой точке

1. 

2. 

3. 

4. 

5. 

31. Прямая является вертикальной асимптотой функция, если

1. 

2. 

3. 

4. 

5. 

32. Прямая является наклонной асимптотой функция , если существуют конечные пределы

1. ,

2. ,

3. ,

4. ,

5. ,

33. Если функция непрерывна, а функция дифференцируема и имеет непрерывную производную, то формула замены переменой в неопределенном интеграле имеет вид

1. 

2. 

3. 

4. 

5. 

34. Если функция непрерывна, а функция дифференцируема и имеет непрерывную производную, то формула замены переменой в неопределенном интеграле имеет вид

1. 

2. 

3. 

4. 

5. 

35. Если какая-либо первообразная функции , то для определенного интеграла справедлива формула

1. 

2. 

3. 

4. 

5. 

36. Объем тела, полученного вращением вокруг ОХ криволинейной трапеции, ограниченной функцией , прямыми и осью ОХ равен

1. 

2. 

3. 

4. 

5. 

37. Как проверяется правильность результата интегрирования:

1. дифференцированием найденной первообразной

2. интегрированием результата

3. вычисляется подынтегральная функция

4. результат проверить не возможно

5. по теореме Лагранжа

38. Как называются перечисленные дроби

1. сложные дроби

2. простейшие дроби

3. не рациональные дроби

4. правильные дроби

5. иррациональные дроби

39. При нахождении интеграла методом подстановки используется формула:

1. 

2. 

3. 

4. 

5. 

40. Метод интегрирования по частям основан на формуле:

1. 

2. 

3. 

4. 

5. 

41. Укажите формулу Ньютона-Лейбница:

1. 

2. 

3. 

4. 

5. 

42. При нахождении определенного интеграла методом подстановки используется формула:

1. 

2. 

3. 

4. 

5. 

43. Интеграл вида ,

где находится с помощью

1. Рекуррентной формулы понижения степени знаменателя

2. Интегрирования

3. Неопределенного интеграла

4. Теоремы Коши

5. Теоремы Лагранжа

44. В каком методе условие, при котором должно выполняться взаимно однозначное соответствие между областями иопределения функцийи, такое чтобы функция принимала все значения.

1. метод интегрирования по частям

2. метод подстановки

3. неопределенный интеграл

4. интегрирования

5. теоремы Лагранжа

45. На какой формуле основан метод интегрирования по частям:

1. 

2. 

3. 

4. 

5. 

46. Укажите формулу интегрирования по частям:

1. 2.3.

4. 5.

1. 1

2. 2

3. 3

4. 4

5. 5

47. По какой формуле можно вычислить площадь криволинейной трапеции ограниченный кривой , прямымии осью Ох:

1.2.3.4.5.

1. 1

2. 2

3. 3

4. 4

5. 5

48. Как называется данная формула:

1. Формула Ньютоно-Лейбница

2. Интегрирования по частям

3. Метод замены переменной в неопределенном интеграле

4. Табличный интеграл

5. Определение неопределенного интеграла

49. Укажите целесообразную подстановку для нахождения интеграла

1. 

2. 

3. 

4. 

5. 

50. Если А –постоянная, то

1. 

2. 

3. 

4. 

5. 

218