начерт геом машиност дневное

Федеральное агентство по образованию Восточно-Сибирский государственный технологический университет

Кафедра «Инженерная и компьютерная графика»

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ

по

начертательной геометрии

для студентов машиностроительных и механических специальностей

Издательство ВСГТУ Улан-Удэ, 2008

3

Студенты машиностроительных и механических специальностей по курсу начертательной геометрии самостоятельно выполняют домашние графические работы. Объем работ зависит от специальности и определяется преподавателем. Все работы распределены по основным темам курса. Выполнение данных работ является основным средством глубокого и всестороннего освоения основных положений теории начертательной геометрии.

К экзаменам допускаются только студенты, выполнившие и защитившие все работы.

Работы выполняются на листах чертежной бумаги формата А3 (420х297) чертежными инструментами, обводятся карандашом. Надписи, обозначения и чертежи выполняются в соответствии с ГОСТами ЕСКД.

Выполнение каждой работы необходимо начинать с проработки лекционного материала по теме и решения достаточного количества задач на практических занятиях. Варианты заданий устанавливаются преподавателем и приведены в приложении к данным методическим указаниям.

Работа №1 «Комплексный чертеж поверхности»

Построить комплексный чертеж 3-х поверхностей по заданным проекциям элементов определителя. Первая поверхность – линейчатая общего вида (цилиндрическая, коническая) или многогранная (призматическая, пирамидальная), вторая – линейчатая с плоскостью параллелизма, третья – поверхность вращения. Варианты заданий приведены в приложении №1.

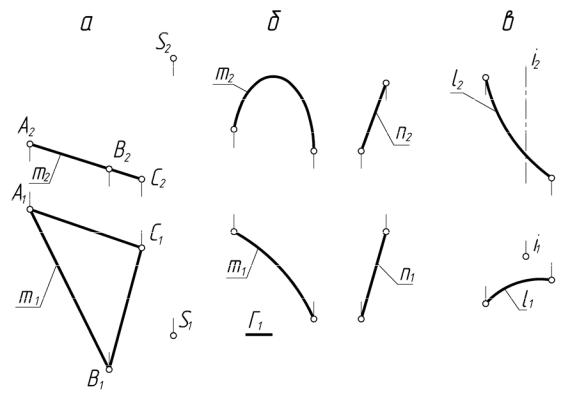
Пример задания поверхностей проекциями элементов определителя показан на рис.1.

Рис.1. а - Θ (m, S) – пирамидальная; б – Ф(m, n, Г1) – коноид, где m – кривая, n - прямая; в – Σ (i, l) – поверхность вращения общего вида

4

Для выполнения этой работы необходимо проработать тему «Поверхности, их образование и задание на комплексном чертеже».

Построить комплексный чертеж поверхности, заданной проекциями определителя, означает:

1.построить проекции некоторого количества образующих или параллелей поверхности;

2.построить проекции линии контура;

3.построить проекции линии обрыва;

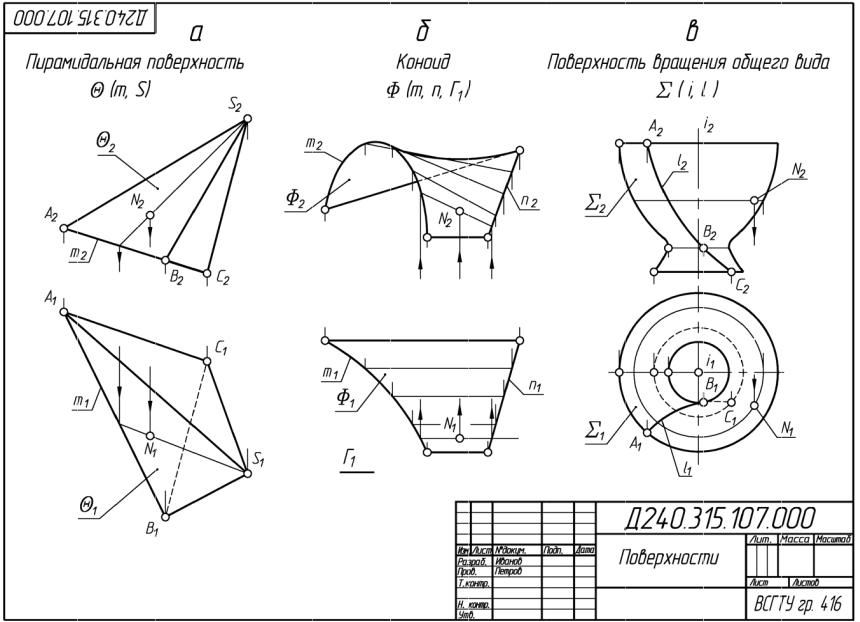
4.определить видимость на построенном чертеже и задать точки, принадлежащие построенным поверхностям. Пример выполнение работы № 1 показан на рис. 2.

В курсе начертательной геометрии изучают те поверхности, которые нашли наибольшее практическое применение. Их условно можно разделить на группы в зависимости от формы образующей линии и закона движения образующей. Здесь необходимо четко представлять себе, какими определителями задаются поверхности каждой группы и алгоритм их построения. Ниже рассматриваются поверхности, которые используются в работах №1, 2.

Многогранная поверхность

К многогранным поверхностям относятся призматические и пирамидальные поверхности. Эти поверхности задаются определителями: направляющая ломаная линия и прямолинейная образующая. Если в процессе перемещения образующая линия проходит через фиксированную точку S (вершину), то образуется пирамидальная поверхность; если образующая перемещается, оставаясь параллельной самой себе, то образуется призматическая поверхность. Направляющая ломаная линия может быть замкнутой или разомкнутой. На рис. 2-а пирамидальная поверхность задана вершиной S и направляющей m (треугольник). Чтобы построить проекции поверхности, проводим ряд промежуточных положений образующей, проходящей через точку S. Обычно для многогранных поверхностей проводят проекции ребер. Для призматической поверхности вместо вершины S задается направление образующей, так как образующая перемещается, оставаясь параллельной самой себе.

Линейчатые поверхности с плоскостью параллелизма (поверхности Каталана)

Эти поверхности образуются при перемещении прямолинейной образующей линии по двум направляющим и в процессе перемещения образующая остается параллельной некоторой наперед заданной плоскости Г, которая называется плоскостью параллелизма. В зависимости от формы направляющих линий, различают следующие поверхности: цилиндроид - обе направляющие кривые линии; гиперболический параболоид, когда обе направляющие линии - скрещивающиеся прямые линии; коноид - одна образующая кривая линия, а вторая образующая прямая. Частный случай коноида - прямой геликоид. Одна направляющая прямая линия перпендикулярна к одной

5

из плоскостей проекций, другая направляющая кривая является винтовой линией, а плоскость параллелизма параллельна плоскости проекции.

На рис. 2-б показано построение коноида. На плоскости П1 проводим ряд промежуточных положений образующей параллельно Г1. По линиям связи строим проекции этих образующих на П2. Затем строим проекции линии контура на П2, как огибающую этих образующих.

Поверхность вращения общего вида

Определителем поверхности являются ось вращения i и любая плоская или пространственная образующая кривая линия. На рис. 2-в показано построение поверхности вращения общего вида. Эта поверхность задана образующей l и осью i. Сначала строим проекции линии обрыва, т.е. проекции верхнего и нижнего оснований. Затем строим проекцию "Горла", для чего из центра вращения i проводим касательную окружность к проекции образующей l1 и находим проекцию точки касания B1. Далее по линии связи находим проекцию B2 и через нее проводим прямую, перпендикулярную к оси вращения i2 , на которую спроецируем касательную окружность. После этого строим ряд промежуточных положений параллелей, для чего на образующей берем любые точки (1..) и строим параллели. Линия контура на П2 определится как огибающая этих параллелей.

Поверхности вращения 2-го порядка

Эти поверхности образуются при вращении прямой или кривой второго порядка вокруг оси симметрии. К поверхностям вращения второго порядка относятся: цилиндр, конус, однополостный гиперболоид вращения, сфера, эллипсоид, параболоид, двуполостный гиперболоид вращения.

Работа №2 «Главные позиционные задачи»

Работа состоит из двух задач (Приложение №2). Требуется построить линию пересечения поверхностей. Видимые контуры поверхностей и линия пересечения обводятся основной сплошной линией, невидимые линии - штриховой линией, дополнительные построения -тонкой сплошной линией.

Выбор метода решения зависит от формы пересекающихся поверхностей и их положения относительно плоскостей проекций. Возможны три случая позиционных задач:

1.обе пересекающиеся поверхности занимают проецирующее положение;

2.одна из поверхностей занимает проецирующее положение, а вторая - общее положение;

3.обе пересекающиеся поверхности занимают общее положение.

В первом случае общий элемент уже задан на чертеже, и решение сводится лишь к обозначению его проекций.

Во втором случае одна из проекций искомого общего элемента непосредственно задана на чертеже. Вторая проекция может быть построена на основе условия принадлежности точек общего элемента поверхности.

6

Рис. 2. Поверхности

7

В третьем случае задача решается методом секущих поверхностей. В качестве секущей поверхности обычно принимают плоскость (чаще плоскости уровня) или сферу. В любом случае секущая поверхность должна быть выбрана такая, чтобы в сечении получились простейшие линии - прямая или окружность. Рекомендуется начинать построение линии пересечения с определения опорных точек (точки пересечения главных меридианов, наивысшие и наинизшие точки, точки, разделяющие видимую часть линии пересечения от невидимой и т.д.). При определении точек пересечения главных меридианов надо сначала выяснить положение общей плоскости симметрии. Определив достаточное количество точек, соединяют эти точки плавной кривой линией, с учетом видимости. При этом надо знать примерно форму линии пересечения. Здесь можно ориентироваться следующим образам:

1.если пересекаются многогранные поверхности, то линия пересечения представляет собой одну, две и более замкнутых ломаных пространственных или плоских линий;

2.если пересекаются многогранная поверхность и поверхность вращения 2-го порядка, то линия пересечения состоит из дуг кривых второго порядка. В частном случае отрезки прямой;

3.если пересекается две поверхности 2-го порядка, то линия пересечения представляет собой замкнутую пространственную кривую 4-го порядка, а в частом случае - две кривые 2-го порядка.

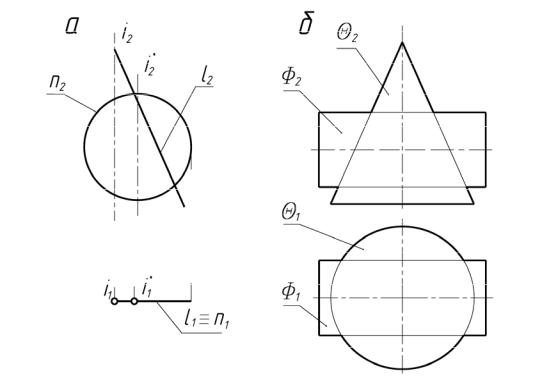
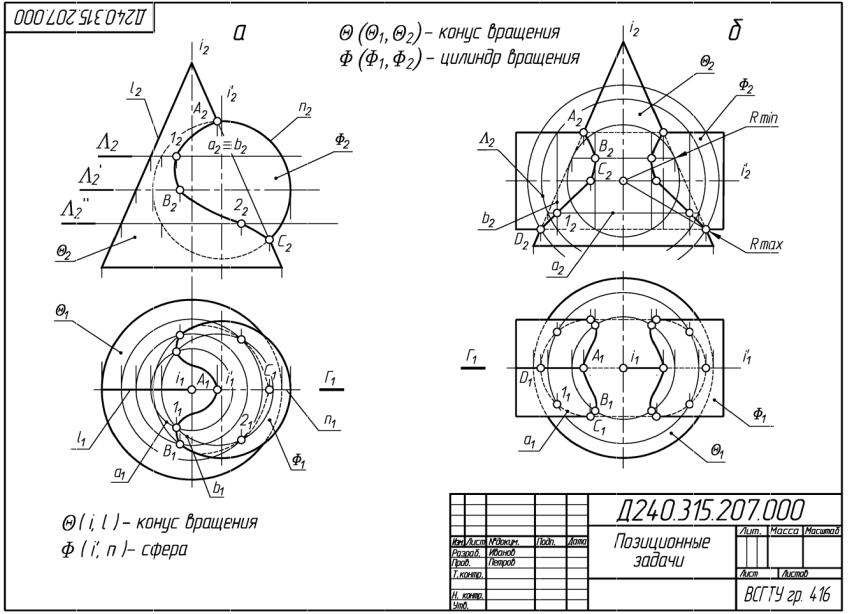
Задача 1. Построить линии пересечения поверхностей конуса вращения Θ и сферы Φ, занимающих общее положение по отношению к плоскостям проекций. Поверхности заданы своими определителями (Рис.3-а).

Анализ условия показывает, что задачу следует решать при помощи вспомогательных секущих горизонтальных плоскостей уровня. Плоскость пересекает обе поверхности по окружностям. Эти окружности на П2 совпадает с проекцией Λ2, а на П1 проецируются без искажения.

Алгоритм решения

1.Находим опорные точки A, C напересечении главных меридианов, так как общая плоскость симметрии Г(Г1) параллельна П2.

2.Выбираем в качестве вспомогательной секущей поверхности горизонтальную плоскость уровня Λ// П1.

3.Рассекаем обе поверхности выбранной плоскостью Λ. Секущая плоскость должна располагаться между опорными точками A и C.

4.Определяем линии, по которым плоскость Λ пересекает заданные поверхности: a = Λ∩Θ и b = Λ∩Ф.

5.На пересечении полученных линий a и b определяем точку 1, принадлежащей искомой линии пересечения.

6.Таким образом, проводя множество секущих плоскостей Λ’, Λ’’ и т. д., находим множество точек, которые соединяем плавной кривой линией.

8

7.На построенной линии пересечения находим опорную точку В и определяем видимость на П1 (Рис.4 а).

Рис.3. а - Θ (i, l) – конус вращения, Φ(i’, n) – сфера;

б - Θ (Θ1, Θ2) – конус вращения, Φ(Φ1, Φ2) - цилиндр вращения

Задача 2. Построить линии пересечения конической Θ и цилиндрической Φ поверхностей вращения, занимающих общее положение по отношению к плоскостям проекций. Поверхности заданы своими проекциями (Рис.3-

б).

Анализ задачи показывает, что её следует решать методом концентрических сфер. При этом, задача должно удовлетворять трем условиям:

1.пересекающиеся поверхности должны быть поверхностями вращения;

2.оси вращения этих поверхностей должны пересекаться, точка пересечения осей является центром сфер;

3.общая плоскость симметрии Г должна быть параллельна одной из плоскостей проекций.

Алгоритм решения

1.Находим опорные точки на пересечении главных меридианов – А, D.

2.Определяем вспомогательную секущую сферу максимального радиуса

Rmах. За Rmах принимают расстояние, от центра сфер до самой удаленной опорной точки D.

3.Определяем вспомогательную секущую сферу минимального радиуса

Rmin. Сфера минимального радиуса должна касаться одной поверхности и пересекать другую.

4.Проводим промежуточную сферу Λ между сферами радиуса Rmах и

Rmin.

9

5.Определяем линию пересечения сферы Λ с поверхностью Ф и с поверхностью Θ: a = Λ∩Θ и b = Λ∩Ф.

6.На пересечении полученных линий a и b определяем точку 1, принадлежащей искомой линии пересечения.

7.Таким образом, проводя множество сфер Λ’, Λ’’ и т. д., находим множество точек, которые соединяем плавной кривой линией.

8.На построенной линии находим опорную точку С и определяем видимость проекций линии пересечения на П1 (Рис.4-б).

Работа №3 «Метрические задачи»

Работа состоит из трех задач. Даны координаты плоскости треугольника Θ(АВС), требуется решить следующие задачи (Приложение №3).

1.Построить плоскость перпендикулярно заданной плоскости Θ и определить линию пересечения этих плоскостей и видимость на чертеже.

2.Построить плоскость Ω, параллельную плоскости Θ, отстоящую от нее на заданном расстоянии, амм.

3.Построить касательную плоскость и нормаль к поверхности. Поверхность для этой задачи взять одну из четырех заданных поверхностей в работе №2 по указанию преподавателя.

Задача 1. Для построения плоскости Ω Θ:

1.Строим перпендикуляр (n Θ) к заданной плоскости. Условия перпендикулярности прямой к плоскости на комплексном чертеже:

n1 h1 и n2 f2.

2.Проводим плоскость Σ через перпендикуляр n и прямую l (n∩l или n//l).

3.Определяем линию пересечения плоскостей с помощью вспомогательных секущих плоскостей;

4.Определяем видимость на чертеже (Рис.5-а).

Задача 2. Построение плоскости Ω параллельной заданной Θ на расст. а.

Алгоритм решения

1.Определяем расстояние от произвольной точки E до плоскости Θ.

2.На натуральной величине этого расстояния откладываем заданную величину а.

3.Через полученную точку F строим плоскость Ω (Рис.5-а).

Задача 3. Построения нормали к поверхности Ф в точке М.

Алгоритм решения

1.Построим касательную плоскость к заданной поверхности в точке М при помощи касательных прямых t, t’.

2.Построим перпендикуляр к касательной плоскости в точке М, который является нормалью n к поверхности Ф (Рис.5-б).

10

Рис. 4. Позиционные задачи