
Начерт.гео-кожа
.pdf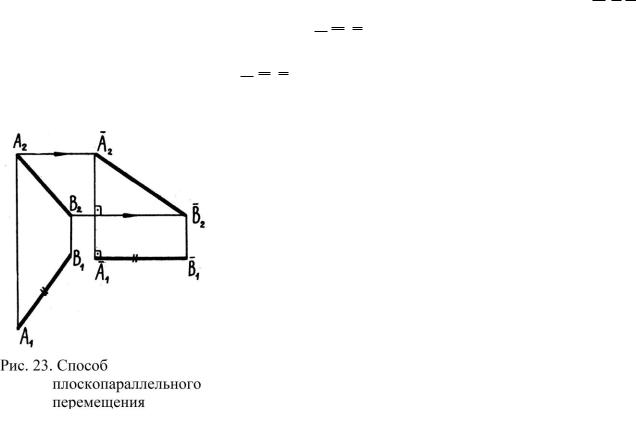
4) Поворачивают плоскость треугольника, занимающую проецирующее положение, так, чтобы она стала параллельной другой плоскости проекций (повернули прямую M2 P2 N2
вокруг проецирующей прямой i, получили M1 N 2 P2 ).
5) Строят вторую проекцию треугольника, которая будет являться натуральной вели-
чиной MNP (в данном случае M1 N 2 P2 .
Вопросы для самоподготовки
1.Дать характеристику понятию «метрические задачи».
2.Какие способы преобразования комплексного чертежа вы знаете?
3.Какова цель использования способов преобразования комплексного чертежа?
4.Рассказать об основных принципах способа плоскопараллельного перемещения. Для решения каких задач он может использоваться?
5.Рассказать об основных принципах способа вращения. Для решения каких задач он может использоваться?
6.Рассказать об основных принципах способа перемены плоскостей проекций. Для решения каких задач он может использоваться?
Домашняя работа №4 «Развертки поверхностей»
Методические указания к выполнению ДР№4
1.Изучить теоретический материал, представленный ниже
2.При возникновении вопросов обратиться к учебной литературе
3.Изучить пример выполнения домашней работы (прил. 4).
4.Выполнить развертку поверхности геометрического тела в соответствии со своим вариантом.
Развертки поверхностей
С развертками поверхностей часто приходится встречаться на производстве, в строительстве и в быту. Для того чтобы изготовить чехол для чемодана, упаковку для продукта, парашют и т.д., необходимо вначале построить развертки геометрических тел (или их отдельных частей), лежащих в основе данных объектов (призма для чемодана, часть шара для парашюта и т.д.). В соответствии с этим знание законов построения разверток поверхностей – важный элемент получения образования для специалиста любого профиля. В курсе начертательной геометрии выполняют построение разверток поверхностей или поверхностей геометрических тел (различие этих терминов повторить по разделам домашней работы №2)
Основные положения и способы построения разверток
Развертка – фигура, полученная в результате совмещения поверхности данного тела с плоскостью. Не для каждой поверхности можно построить ее точную развертку. Развертывающимися называют поверхности, которые можно совместить с плоскостью без
21

растяжения, сжатия, складок и разрывов. В противном случае поверхности называют неразвертывающимися. Это один из признаков классификации поверхностей (рис.13).
К развертывающимся относятся все многогранные поверхности. Разверткой многогранной поверхности является плоская фигура, полученная последовательным совмещением с одной и той же плоскостью всех ее граней. Поэтому построение развертки многогранника сводится к определению натуральной величины его отдельных граней. Из кривых поверхностей к числу развертывающихся относятся только те линейчатые поверхности, у которых касательная плоскость касается поверхности во всех точках ее прямолинейной образующей. Это значит, что у развертывающейся линейчатой поверхности касательная плоскость во всех точках одной и той же образующей постоянна. Если у поверхности в различных точках одной и той же образующей можно построить разные касательные плоскости, то она является неразвертываеющейся.
Таким образом, к развертывающимся поверхностям можно отнести цилиндрические, конические и торсовые (рис. 24 а, б, в соответственно). Остальные поверхности считаются неразвертывающимися.
Рис. 24. Развертывающиеся поверхности.
Наиболее широко применяют 3 способа построения разверток:
1)раскатки,
2)нормального сечения,
3)аппроксимации (один из примеров – способ триангуляции5).
Выбор способа зависит от вида поверхности и расположения ее относительно плоскостей проекций.
Первый способ (раскатки) целесообразно применять для построения развертки многогранника, когда одна из граней параллельна одной из плоскостей проекций. К примеру, дана проецирующая призма (рис. 25). Здесь и далее строим развертки для геометрических тел.
Два основания призмы (АВСD и А'В'С'D') параллельны горизонтальной плоскости проекций П1. Значит, отрезки АВ, ВС, CD, DA (ребра оснований) проецируются на П1 в натуральную величину (аналогично для второго основания). На П2 также имеем натуральные величины вертикально расположенных ребер АА', ВВ', СС', DD'. Считаем, что плоскость развертки совпадает с гранью AA'DD' призмы, с этой же плоскостью совмещаем другие грани призмы, как это показано на рисунке. Грань СС'ВВ' предварительно совмещаем с гранью АА'ВВ'. Линии сгибов в соответствии с ГОСТ 2.303–68 проводим тонкими
5От лат. triangulum – треугольник. Поверхность, для которой строят развертку, аппроксимируют к более простой поверхности. Если аппроксимирующая поверхность состоит из треугольников, способ называют способом триангуляции.
22
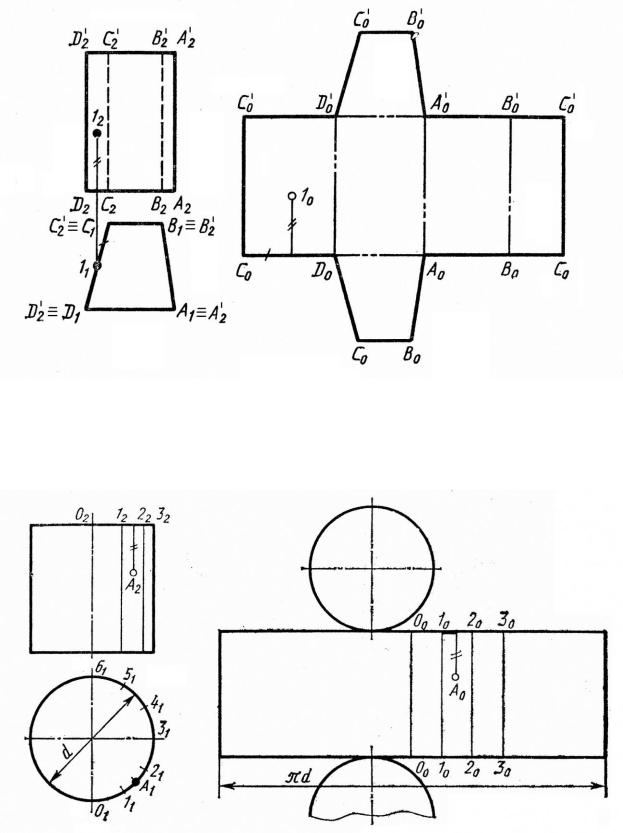
штрихпунктирными линиями с двумя точками толщиной s/3 ... s/2. Точки на развертке принято обозначать такими же буквами, как и на комплексном чертеже, но с индексами 0 (ноль). Развертку принято строить так, чтобы к наблюдателю была обращена лицевая сторона поверхности. Это условие важно соблюдать потому, что некоторые материалы (кожа, ткани) имеют две стороны: лицевую и оборотную.
Рис. 25. Построение развертки проецирующей призмы
К одной из граней боковой поверхности пристраиваем основания призмы ABCD и A'B'C'D'. Если на поверхности призмы задана точка 1, то на развертку переносим ее с помошью двух отрезков, помеченных на комплексной чертеже одним и двумя штрихами.
Рис. 26. Построение развертки проецирующего цилиндра
23

Развертку поверхности проецирующего на П1 цилиндра вращения строим аналогично (рис. 26). Делим поверхность цилиндра на определенное число равных частей, например, на 12, и развертываем вписанную поверхность правильной 12-угольной призмы (для упрощения точки верхнего и нижнего основания цилиндра обозначены одинаково). Длина развертки при таком построении получается несколько меньше действительной длины развертки. Этот способ построения называется способом аппроксимации (если аппроксимирующая поверхность имеет треугольные грани, то способ называется способом триангуляции). Если требуется точность при построении развертки, можно применить графоаналитический способ. Диаметр окружности основания цилиндра умножаем на число π = 3,14. Полученный размер используется в качестве длины развертки, а высота цилиндра берется непосредственно с комплексного чертежа. К развертке боковой поверхности пристраиваем основания цилиндра. Если на поверхности цилиндра задана точка А, например, между первой и второй образующими, то ее место на развертке находим с помощью двух отрезков (на комплексном чертеже): хорды длиной 11А1 и отрезка 22А2, откладывая их соответственно на развертке.
Рис. 27. Построение развертки пирамиды
Значительно труднее построение развертки пирамиды (рис. 27). Ее ребра SA и SC являются прямыми общего положения и проецируются на обе плоскости проекций с искажением. Прежде чем строить развертку, необходимо найти действительную величину каждого ребра. Величину ребра SB находим путем построения его третьей проекции, поскольку это ребро параллельно плоскости П3. Ребра SA и SC поворачиваем вокруг горизонтально проецирующей оси, проходящей через вершину S в положение, при котором оси становятся параллельными фронтальной плоскости проекций П2 (таким же способом может быть найдена действительная величина ребра SB). После поворота фронтальные проекции S2A2 и S2C2 будут равны действительной величине ребер SA и SC. Стороны основания пирамиды, как горизонтали, без искажения проецируются на плоскость проекции П2. Имея три стороны каждой грани и пользуясь способом засечек, строим развертку. Построение начинаем с передней грани. На горизонтальной прямой откладываем отрезок
24

А0С0 = A1C1; первую засечку делаем радиусом A0S0 = А2'S2, вторую — радиусом C0S0 = C2'S2; в пересечении засечек получаем точку S0. За базу принимаем сторону А0S0, из точки А0 делаем засечку радиусом А0В0 = А1В1, а из точки S0 – засечку радиусом S0В0 = S3B3, в пересечении засечек получаем точку В0. Аналогично к стороне S0С0 пристраиваем грань S0В0С0. В заключение к стороне А0С0 пристраиваем треугольник основания А0С0В0. Длины сторон этого треугольника можно взять непосредственно с развертки, как показано на рисунке.
Развертку конуса вращения (рис. 28) строим так же, как и развертку пирамиды (способ триангуляции). Делим окружность основания на равные части, например, на 12 и представляем, что в конус вписана правильная 12-угольная пирамида (первые три грани показаны на чертеже).
Рис. 28. Построение развертки конуса.
Разрезаем поверхность конуса по образующей S6 (на П2 это невидимая часть конуса). Развертка конуса изображается сектором круга, у которого радиус равен длине ℓ образующей конуса. Все образующие данного конуса равны, действительная величина ℓ образующей равна фронтальной проекции левой (или правой) образующей (поскольку именно они являются отрезками фронталей). От точки S0 по вертикали откладываем отрезок S0O0 = ℓ. Этим радиусом проводим дугу окружности. От точки О0 откладываем отрезки О010 = О111, 1020 = 1121 и т.д. Отложив шесть отрезков, получаем точку 60, которую соединяем с вершиной S0. Аналогично строим левую часть развертки; снизу пристраиваем основание конуса.
Если требуется нанести на развертку точку В, то через нее проводим образующую SB (в данном случае S2); эту образующую наносим на развертку S020, вращая образующую с точкой В против часовой стрелки до совмещения ее с образующей S3 (S232), находим действительное расстояние S2B2 и откладываем его от точки S0. Найденные отрезки помечены на чертежах тремя штрихами.
25

Развертка ненаклонного конуса может быть построена быстрее и точнее, поскольку известно, что угол сектора развертки α = 360° R/ ℓ, где R — радиус окружности основания, а ℓ — действительная длина образующей конуса.
Как следует из вышесказанного, развертки для развертывающихся поверхностей могут быть построены точно или с приближением, в зависимости от цели построения.
Для непроецирующих поверхностей, или поверхностей, расположенных с наклоном к плоскостям проекций, чаще всего строят развертку только поверхности, без оснований.
Например, в случае построения развертки отсека поверхности эллиптического конуса, ограниченного окружностью, лежащей в горизонтальной плоскости уровня и эллипсом n в профильной плоскости уровня (рис. 29), можно построить развертку поверхности, причем только приближенного размера. На рисунке выполнены построения с помощью способа триангуляции одной половины (видимой части конуса). Длины образующих определены вращением вокруг горизонтально-проецирующей оси i (i1, i2), проходящей через вершину конуса S, до положения, параллельного П2 для каждой образующей. На рисунке выполнены также построения по определению точки М, лежащей на поверхности конуса.
Рис. 29. Построение приближенной развертки конической поверхности
Вопросы для самоподготовки
1.Дать определение термина «развертка поверхности».
2.Привести примеры необходимости выполнения разверток поверхностей.
3.Пояснить смысл выражений «развертка поверхности», «развертка поверхности геометрического тела».
4.Назвать способы построения разверток.
5.Охарактеризовать способ триангуляции.
Домашняя работа №5 «Аксонометрические проекции»
Методические указания к выполнению ДР№5
1.Изучить теоретический материал, представленный ниже.
2.При возникновении вопросов обратиться к учебной литературе.
26

3.Изучить способы выполнения прямоугольной изометрии (рис. 32, пояснения в тексте).
4.Проработать способ выполнения эллипсов (рис.33).
5.Выполнить работу в соответствии с вариантом, образец этапов выполнения представлен в Приложении 5.
Аксонометрия – в переводе с греческого «измерение по осям» (―axcon‖ – ось, ―metreo‖– измеряю). Аксонометрической проекцией объекта называют условное изображение, когда предмет вместе с одной из его ортогональных проекций и осями координат6, к которым она отнесена, проецируется параллельными лучами на какую-либо плоскость, называемую картинной. Аксонометрические проекции используют для получения наглядного изображения объекта. В соответствии с ГОСТ 2.317-69 при построениях обычно применяют какую-либо из пяти разновидностей аксонометрических проекций, отличающихся определенной комбинацией направлений аксонометрических осей и аксонометрических масштабов (рис. 24). Наибольшее распространение получили прямоугольные (ортогональные) аксонометрические проекции. При проецировании на картинную плоскость происходит искажение размеров предмета, поскольку натуральные оси координат расположены под определенными углами к картинной плоскости.
Отношение аксонометрического масштаба к соответствующему натуральному называют показателем искажения (коэффициентом искажения). Подсчитано, что наглядное изображение предмета будет вычерчено в реальную величину в изометрической прямоугольной проекции, если при откладывании натуральных отрезков их величину умножать на коэффициент 0,82. Однако для удобства построения этот коэффициент заменяют на так называемый приведенный коэффициент искажения, равный единице. При этом аксонометрическое изображение получается увеличенным в 1,22 раза (1 : 0,82 = 1,22).
В прямоугольной диметрии коэффициенты искажения по двум осям (X, Z) составляют 0,94; по оси Y – 0,47, приведенные коэффициенты искажения соответственно 1 и 0,5.
На рисунке 31 выполнено построение шестиугольной призматической поверхности в прямоугольной изометрии. На чертеже показаны проекции осей натуральной системы координат (O1X1Y1 и O2X2Z2), аксонометрические оси O'X'Y'Z'. Построение аксонометрической проекции объекта сводится к построению аксонометрических проекций его вершин и ребер. Построение начинают с нижнего основания (нижней линии обрыва). На чертеже показано, какие отрезки откладываются при построении аксонометрических проекций.
При выполнении аксонометрических проекций нужно помнить об алгоритме:
1.Любому чертежу в аксонометрической проекции должен предшествовать чертеж, выполненный в ортогональных проекциях.
2.Ось Z на картинную плоскость проецируется всегда вертикально, оси OX и OY строят строго под углом, рекомендуемым для данного вида аксонометрии.
3.Все измерения выполняются только по осям или параллельно осям.
4.Все прямые линии, параллельные между собой или параллельные осям симметрии на ортогональном чертеже, остаются параллельными в аксонометрии.
Для выяснения внутренней формы объекта выполняют вырез ¼ или ⅛.
Схематично на рисунке 32 представлены 2 способа построения изображений детали и ее изображение, выполненное в прямоугольной изометрии. Обычно построения выполняют с нижнего основания детали (2 способ), однако, зная, что ¼ детали будет удалена, целесообразнее выполнять построения именно от места выреза (1 способ). При этом, однако, не следует забывать о построении эллипсов: важно, чтобы точки, найденные измерением по осям, совпадали с аналогичными точками при построении эллипсов.
6 Оси, к которым прикрепляют ортогональное изображение предмета, называют натуральной си-
стемой координат
27

Аксонометрические
проекции
Прямоугольные (проецирующие лучи ┴ картинной плоскости)
изометрические
Z
1:1
1200 1200 диметрические
Фронтальная
изометрическая
Z
1:1
Косоугольные (проецирующие лучи не перпендикулярны картинной плоскости)
Фронтальная
диметрическая
Горизонтальная |
Z |
изометрическая |
1:1 |
|
1 |
X |
1: |
|
 1200
1200 
1: 1
Y |
1:1 |
Z |
|
X 1:1 |
|
|
|
|
|||||
|
|
|
|
|||
|
|
|
|
|
||
|
7010' |
|
|
|
|
|
1:1 |
|
|
|
41025' |
|
|
|
|
|
|
|||
X |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
1: |
|
|
|
|
|
|
2 |
|
|
Y
450
1:1
Y
1 |
: |
1 |
|
|
X
1:1
Z X 1:1
300
1:1
Y
450
1:2
Y
|
Изображение куба в аксонометрических проекциях |
Z |
|
Z |
Z |
||
|
|||
|
X |
X |
|
|
|
||
|
Z |
|
|
|
Z |
|
|
X |
Y |
|
Y |
Y |
|
X
Y
Y
X
Рис. 30. Виды аксонометрических проекций
28

Рис. 32. Последовательность выполнения изображений в прямоугольной изометрии
При построении аксонометрических изображений особое внимание следует уделять построению окружностей, которые на ортогональном чертеже являются проекциями цилиндрических или конических тел, отверстий и т.д. Результатом проецирования окружности на картинную плоскость является эллипс (кроме некоторых случаев косоугольной аксонометрии).
На рисунке 33 показано расположение эллипсов на картинной плоскости в зависимости от того, на какой плоскости проекций на ортогональном чертеже была окружность (для прямоугольной изометрической проекции). В этом случае при построении размер большой оси эллипса АВ = 1,22d, малой СD = 0,71d, где d - диаметр изображаемой окружности. Размеры большой и малой осей эллипсов можно определить также путем геометрических построений.
Построение эллипсов требует применения лекал. На практике вместо эллипсов вычерчивают четырехцентровые овалы. Построение овалов одним из способов представлено на рисунке 33.
Вначале строят хорду на окружности, для которой выполняют овал (рисунок справа). Далее проводят окружности радиусом, равным половине большой и малой оси соответственно (тонкие линии на рисунке слева). Как видно из рисунка, радиусы R и R', с помощью которых выполняют построения овалов, можно определить из построений. Для их определения можно также использовать формулы: R = (AB + CD) / 2 и R' = (AB – CD) / 2.
Вопросы для самоподготовки
1.Дать понятие аксонометрии.
2.Что такое «картинная плоскость»?
3.Назвать способ проецирования, используемый при выполнении аксонометрических проекций (повторить материал ДР№1).
4.Объяснить различие между терминами «коэффициент искажения», «приведенный коэффициент искажения».
5.Для каких целей выполняют вырез ¼ аксонометрического изображения?
6.Назвать виды аксонометрических проекций.
7. Какие способы построение эллипсов при выполнении аксонометрических проекций вы знаете?
29
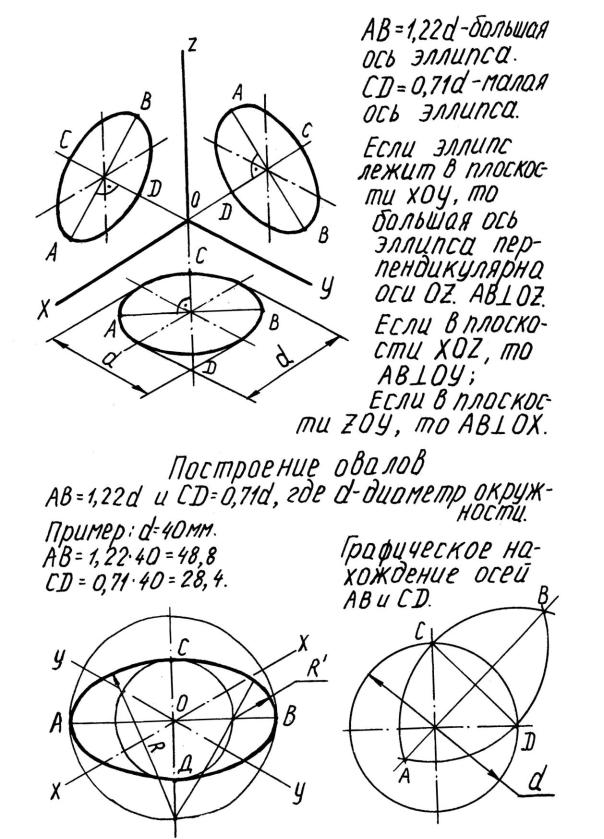
Рис. 33. Построение овалов в прямоугольной изометрии
30
