вопрос 1 идеальная несжимаемая жидкость - воображаемая жидкость, не обладающая ни сжимаемостью, ни вязкостью. (напр. спирт,ауетон, вода). Уравнение неразрывности струи: S1V1=S2V2, где s1 - первое сечение трубки, S2- второе v1, v2 - скорости жидкостей. Его физический смысл заключается в том, что жидкость нигде не накапливается, т. е. за одинаковый временной интервал в трубку тока втекает и вытекает равное количество жидкости.

№1 Идеа́льная несжима́емая жи́дкость — модельный объект механики сплошной среды и гидравлики, жидкость/сплошная среда фиксированной плотности, обладающая нулевой вязкостью. Несжимаемая жидкость модель среды, плотность которой остаётся неизменной при изменении давления и является её физической характеристикой. Для Н. ж. скорость распространения малых возмущений (скорость звука) равна бесконечности, поэтому любое возмущение, вносимое в какую-либо точку потока, мгновенно передаётся всему полю течения. В реальных жидкостях и газах скорость звука имеет конечное значение. В стационарном потоке достаточным условием для применения модели Н. ж. является условие малости скорости движения по сравнению со скоростью звука. В нестационарном потоке, кроме этого, необходимо, чтобы время, в течение которого звук, сигнал пройдёт расстояние, равное характерному линейному размеру, было много меньше времени, в течение которого заметно изменяется движение среды. В силу сказанного модель Н. ж. свойственна многим прикладным задачам (движение кораблей в воде, полёт самолёта с малыми дозвуковыми скоростями, на режиме взлёта и посадки и т. д.), а её использование значительно упрощает их решение. Поле течения идеальной Н. ж. определяется неразрывности уравнением и Эйлера уравнениями; энергии уравнение выпадает из рассмотрения из-за постоянства удельной внутренней энергии среды. Для вязкой Н. ж. обычно предполагается постоянство коэффициента переноса ; это позволяет сначала проинтегрировать совмещенное уравнение неразрывности и количества движения уравнение, а затем для найденных полей скоростей и давлений — уравнение притока теплоты, определяющее поле температуры. Однако для некоторых Н. ж. зависимость коэффициента переноса от температуры является очень сильной, поэтому при исследовании их движения эту систему уравнений необходимо решать совместно. Уравнение неразрывности для несжимаемой жидкости Sv = const где S - площадь поперечного сечения трубки тока жидкости; v - скорость течения жидкости.

вопрос 2 уравнение Бернулли - одно из основных уравнений гидромеханики, которое при установившемся движении несжимаемой идеальной жидкости в однородном поле сил тяжести имеет вид: Gh + p/ρ + v2/2 = C, (1) где v — скорость жидкости, ρ — её плотность, р — давление в ней, h — высота жидкой частицы над некоторой горизонтальной плоскостью, g — ускорение свободного падения, С — величина, постоянная на каждой линии тока, но в общем случае изменяющая своё значение при переходе от одной линии тока к другой. Сумма первых двух членов в левой части уравнения (1) равна полной потенциальной, а третий член — кинетической энергиям, отнесённым к ед. массы жидкости; следовательно, всё уравнение выражает для движущейся жидкости закон сохранения механической энергии и устанавливает важную зависимость между v, p и h. Например, если при неизменной h скорость течения вдоль линии тока возрастает, то давление падает, и наоборот. Этот закон используют при измерении скорости с помощью трубок измерительных и при других аэродинамических измерениях. Уравнение Бернулли представляют также в виде h + p/γ + v2/2g = C или γh + p + ρv2/2 = C (2) (где γ =ρg — удельный вес жидкости). В 1-м равенстве все слагаемые имеют размерность длины и называются соответствующей геометрической (нивелирной), пьезометрической и скоростной высотами, а во 2-м — размерности давления и соответственно именуются весовым, статическим и динамическим давлениями.

вопрос 3 идеальная жидкость - это жидкость, рассматриваемая в условиях, когда несущественны процессы вязкой диссипациии теплопереноса. Коэффициент вязкости жидкости - это единица связанная с ее способностью выдерживать поперечную силу. Веществам с высоким коэффициентом вязкости требуется большая поперечная сила для сдвигания жидкостей, чем веществам с меньшим коэффициентом вязкости. САНТИПУАЗ (cPo) наиболее удобная единица измерения коэффициента вязкости. Узнать абсолютную вязкость можно таким прибором, как вискозиметр. Им измеряется сила, необходимая для вращения микрометрического винта/ валика/ оси. Другие единицы измерения вязкости, такие, как сантистокс (cs) Salbolt Second Universal (SSU) – единицы измерения кинематической вязкости, при которой определенная сила тяжести жидкости влияет на измеряемую вязкость. Кинематические вискозиметры обычно измеряют силу тяжести жидкости, стекающей по калиброванной трубке, учитывается время течения потока. К сожалению, вязкость не является постоянным, фиксированным свойством жидкости. Эта характеристика, изменяющаяся в зависимости от плотности жидкости и типа насоса. В работе насоса естественным считается снижение вязкости при увеличении температуры.

вопрос 4 закон Гайгена-Пуазейля - обьемный расход жидкости в трубе пропорционален четвертой степени радиуса трубы и градиенту давления и обратно пропорционален коэфф. вязкости жидкости. z - гидравлическое сопротивление p1 - давление в начале отрезка p2 - давл. в конце отрезка такая штука похожая на n, только с хвостиком снизу - коэфф. вязкости жидкости Q — расход жидкости в трубопроводе; D — диаметр трубопровода;

вопрос 5 Физические свойства крови Теплопроводность, которая обеспечивает перенос теплоты, образуемой в результате жизнедеятельности во всех частях организма, и способствует тем самым поддержанию постоянной температуры тела у теплокровных животных. Вязкость крови значительно больше, чем у воды. Закон Стокса, пользуясь формулой которого можно подсчитать коэффициент вязкости плазмы крови. η=2/9*(ρ-ρ_ж)/ν gR^2 Различие между вязкости плазмы в относительных единицах и вязкость цельной крови определяется величиной гематокрита и может быть описано уравнением Хатчека, которое имеет вид: η_к=η_п/(1-√Ф) \ Другими словами, гематокрит – это суммарный объем форменных элементов в процентах по отношению ко всему объему крови. Плотность – масса тела, содержащаяся в единице объема. Скорость оседания эритроцитов (мм/ч) Масса крови Количество эритроцитов в 1 мкл крови, млн

№6.

Сердце как механическая система. Метод Короткова — метод измерения давления крови.

1. Сердце является основным источником энергии, обеспечивающим движение крови в сосудистой системе. Оно переводит химическую энергию, заключённую в молекулах АТФ, образующихся в процессе гликолиза и окислительного фосфолирования в сердечной мышце, в механическую работу. Таким образом, сердце представляет собой хемоэлектромеханический насос, работающий в импульсном режиме. В отличие от насосов, применяемых в технике, сердце работает в течение всей жизни организма.

2. Для измерения артериального давления широко применяется метод Короткова, разработанный им в 1905 г. Метод основан на прослушивании шумов, создаваемых пульсовыми волнами.

Манжету накладывают на плечевую, височную, бедренную артерии или же на основание хвоста животного и накачивают в неё воздух, пока в артерии не прекратится ток крови и не исчезнет пульс. Затем воздух из манжеты понемногу выпускают. Когда давление на артерию станет равным систолическому, кровь начинает проталкиваться через сдавленную артерию, и в ней создаётся турбулентный поток, сопровождающийся шумами. Эти шумы хорошо прослушиваются через фонендоскоп и по манометру регистрируется соответствующее этому моменту систолическое давление. Показания манометра в момент исчезновения шумов (при дальнейшем снижении давления) соответствуют минимальному (диастолическому) давлению.

Вопрос №7.Капиллярный метод измерения вязкости жидкостей, крови.Измерение вязкости жидкостей и крови осуществляется при помощи капиллярного вискозиметра, предназначенного для измерения коэффициента вязкости.Коэффициент вязкости жидкости ƞ.Находится по формуле:

№8.

Термодинамикой называют раздел физики,в котором изучают закономерности тепловой формы движения материи и связанных с ней физических явлений. Состояние системы определяется совокупностью ее параметров, которые представляют собой поддающиеся измерению макроскопические физические величины. К важнейшим параметрам относятся объем V,температура T,давление p, а также электрическая поляризация, намагниченность и др. Уравнение, которое связывает между собой объем, температуру и давление в состоянии термодинамического равновесия, называют термическим уравнением состояния. Общий вид уравнения состояния: ƒ(p,T,V)=0.Примером уравнения состояния для идеального газа может служить уравнение Менделеева-Клайперона: pV=m/μ RT Термодинамическим процессом называют переход системы от одного равновесного состояния в другое в результате ее взаимодействия с внешними телами. Обратным называют такой процесс, который может протекать в прямом и обратном направлениях, причем так, что система возвращается в исходное состояние без того, чтобы в окружающих телах происходили какие-либо изменения, а возвращение происходит через ту же последовательность промежуточных состояний,что и прямом процессе, но в обратном порядке . Процесс обратим,если его можно рассматривать как непрерывный ряд равновесных состояний, т.е он должен быть медленным по сравнению с временим релаксации данного термодинамического состояния. Реальные процессы в природе протекают с конечной скоростью, и поэтому они необратимы, происходит с рассеянием энергии. Любой процесс, при котором энергия, хотя бы частично, превращается в теплоту, необратим, потому что часть энергии, перешедшая в теплоту при прямом процессе, не может вернуться в систему самопроизвольно при обратном процессе, что противоречило бы второму началу термодинамики. Необратимые процессы могут протекать самопроизвольно только в одном направлении; процессы диффузии, теплопроводности и др. Первое начало термодинамики представляет собой закон сохранения энергии для систем, в которых основное значение имеют тепловые процессы. Суть его в том, что теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на работу совершаемую силами, приложенными со стороны системы к внешним телам: Q=∆U+A Q-теплота U-внутренняя энергия A-работа Живой организм выделяет теплоту в окр.среду, т.е обладает свойством теплопродукции за счет энергии, полученной от продуктов питания или фотосинтеза, и, кроме этого, выполняет различные виды работы: механическую, электрическую, химическую, осмотическую. В конечном счете все виды энергии превращаются в теплоту, которая выводится в окружающее пространство, а энтропия системы возрастает. Хим. работа совершается клеткой при синтезе высокомолекулярный вещ-в из низкомолекулярных, которые поступают в организм извне, при воспроизводстве клеток, а также при др. происходящих в организме хим. реакций. Механ. работа выполняется мышцами при их сокращении и затрачивается на перемещение всего тела или его отдельных органов против внешних механ. сил. Электрическая работа имеет место в мембранах клеток и клеточных органелл при генерировании биопотенциалов, при проведении возбуждения в нервных клетках. Оматич. работа совершается при активном транспорте вещ-в через клеточные мембраны против направления градиента концентрации этих вещ-в. В живом организме энергия выделяется при окислении пищевых продуктов – белков, жиров, углеводов. Энергия, образующаяся при окислении продуктов питания выделяется в виде теплоты, которую условно подразделяют на первичную(основную) и вторичную(активную). Первичная теплота выделяется сразу же после окисления и не зависимо от того, совершает ли организм какую-либо работу или нет. Это теплота идет на нагревание организма и рассеивается в окр. пространстве.

№ 9

Существует 2 эквивалентные формулировки второго закона термодинамики:

• Постулат Клаузиуса. Процесс, при котором не происходит других изменений, кроме передачи теплоты от горячего тела к холодному, является необратимым, то есть теплота не может перейти от холодного тела к горячему без каких-либо других изменений в системе. Это явление называют рассеиванием или диссипацией энергии.

• Постулат Кельвина. Процесс, при котором работа переходит в теплоту без каких-либо других изменений в системе, является необратимым, то есть невозможно превратить в работу всю теплоту, взятую от источника с однородной температурой, не проводя других изменений в системе.

Вопрос №10.

1).Понятие об энтропии и термодинамической вероятности.

2).Второе начало термодинамики в биологии.

3).Формула Пригожина.

4).Негэнтропия.

1).Энтропия – разность двух значений определенной функции системы до и после отдачи тепла.

(физический смысл энтропии – в случае, когда материальная система находится в равновесии, элементарные частицы, из которых состоит эта система, находятся в неуправляемом состоянии, и совершают разные хаотичные движения).

dS — приращение энтропии;

δQ — минимальная теплота подведенная к системе;

T — абсолютная температура процесса;

Термодинамическая вероятность – количество микросостояний частиц, реализующих макросостояние молекулярной системы.

Термод. вероятность. – W.

S = k*ln*W – связь между термодинамической вероятностью и энтропией.

k – постоянная Больцмана.

k = 10⁻²³ Дж/л

2).Второе начало термодинамики в биологии.

Второе начало термодинамики – закон, согласно которому невозможны такие процессы, единственным конечным результатом которых явилось бы отнятие от некоторого тела определенного количества тепла и превращения этого тепла полностью в работу.

Второе начало термодинамики (в формулировке неубывания энтропии) иногда используется критиками эволюционной теории с целью показать, что развитие природы в сторону усложнения невозможно. Однако, подобное применение физического закона является некорректным, так как энтропия не убывает только в замкнутых системах (сравн. с диссипативной системой), в то время как живые организмы и планета Земля в целом являются открытыми системами.

3). Формула Пригожина.

Теорема Пригожина – стационарному состоянию системы соответствует минимальное производство энтропии.

11

Все живые организмы с позиции термодинамики являются неравновесными (сохраняющие разность потенциалов) термодинамическими системами, в которых имеется соответствие между тем количеством вещества и энергии, которое она получает извне и возвращает обратно (9,14). Однако такой чисто энергетический подход к системе не объясняет цели происходящего обмена. Ответ на этот вопрос дает второй закон термодинамики, связывающий необходимость данного обмена с выполнением системой работы по уменьшению энтропии, непрерывно нарастающей за счет потерь в связи с теплообменом, броуновским движением молекул, старением молекул,

В закрытой термодинамической системе (неживая природа) прирост энтропии всегда положителен (система стремится к максимуму беспорядка и минимуму свободной энергии). В живом организме как в открытой стационарной системе прирост энтропии стремится к нулю и формируется как следствие сопряженных посредством условий Коши-Римана двух взаимно дополняющих процессов: спонтанного роста энтропии за счет термодинамических процессов (St) и процессов негэнтропии (Sн), всегда идущих с понижением энтропии. При этом:

Sн= А/Т lnI, где Sн - негэнтропия; А-минимальная работа;Т - абсолютная температура; I - информация (закон адаптации) (14).

St = k lnW,

где St - рост энтропии за счет спонтанных термодинамических процессов; k -постоянная Больцмана; W - статистическая вероятность.

Для живых систем, где плотность распределения вещества не однородна, второй закон тер модинамики записывается по следующей схеме

т.е. , где: - расход энергии во времени, - выделение тепла во времени, и -соответственно обозначают термодинамическую силу и термодинамическую скорость какого-либо рабочего процесса i

Уникальность живых термодинамических систем заключается в том, что они обладают процессами, в ходе которых происходит понижение энтропии (SН). Возможность возникновения в живызх системах процессов, ведущих к понижению энтропии, тесным образом связана с открытостью и неравновесностью стационарной системы. По сути, живой организм за счет открытости и неравновесности системы работает в режиме вечного двигателя, постоянно компенсируя рост термодинамической составляющей энтропии за счет спонтанных термодинамических процессов, понижением энтропии в ходе негэнтропийных процессов . При этом интенсивность снижения энтропии находится в прямой зависимости.

№12

3 вида теплопередачи:

Теплопроводность — это перенос энергии от более нагретых участков тела к менее нагретымв результате теплового движения и взаимодействия частиц.           Хорошую теплопроводность имеют металлы, у жидкостей теплопроводность невелика, и малую теплопроводность имеют газы. Степень теплопроводности тел учитывается при конструировании машин, в строительном деле, холодильных установках.           Конвекция — это процесс теплопередачи путем переноса энергии потоками жидкости или газа. Явление конвекции проявляется при отоплении и охлаждении жилых помещений, при образовании тяги в печных и заводских трубах, а также ветров в атмосфере.           Излучение — это процесс переноса энергии от одного тела к другому с помощью тепловых (инфракрасных), видимых и других лучей. При одной и той же температуре тела с темной поверхностью сильнее излучают (поглощают) энергию, чем со светлой. Это явление учитывается человеком в быту (светлые тона одежды в теплые периоды года), в технике (окраска холодильников, самолетов, космических кораблей), в земледелии (парники и теплицы).

№13

. виды теплообмена в живых организмах,их сущность. Терморегуляция организма.

Живой организм представляет собой систему, в которую непрерывно поступает энергия из окружающей среды и из которой выделяется такое же ее количество. Изменения соотношения между величинами продукции и отдачи тепла за определенный промежуток времени ведет к колебаниям температуры. Однако многие животные способны поддерживать постоянную температуру тела. В этом процессе участвует большое количество сложных регулирующих процессов. Превращения энергии в организме очень сложны, и они не всегда сопровождаются немедленным переходом всей освобождающейся энергии в тепло. Распределение тепла по организму идет не равномерно, а температура различных органов и тканей также не постоянна.

В организм животных поступает энергия, содержащаяся в питательных веществах корма.

Эта энергия должна обеспечивать расходы на поддержание жизни и синтез определенной продукции (молока, яиц, шерсти, отложений белка и жира в теле).

Наибольшее постоянство температуры присуще крови, мозгу, сердцу и печени, тогда как температура кожи может меняться более значительно под действием внешних факторов среды и физиологических функций организма. Благодаря этому в организме устанавливается динамическое равновесие.

Энергия в организме образуется благодаря окислению белков, жиров и углеводов.

Например, в глюкозе количество энергии, заключенной между атомами С, Н и О, составляет около 2871,2 кДж (686 ккал) на 180 г глюкозы.

Эта энергия освобождается при окислении.

С6 Н12 О6 + 6О2____6Н2О = 6СО2 + 2871,2 кДж

1 Дж = 0,239 или 1 ккал = 4,187 Дж.

Энергия, используемая для поддержания жизни, трансформируется в конечном итоге в тепло основного обмена. У продуктивных животных часть обменной энергии корма идет на поддержание жизнедеятельности и теплопродукцию, остальная часть дает величину чистой энергии, которая используется для образования разных видов продукции. Отложение энергии в организме растущих и откармливаемых животных происходит в форме белка и жира. Лактирующая корова превращает чистую энергию корма в энергию составных частей молока. Другими видами продукции является мышечная работа, образование шерсти и яиц. Эффективность трансформации обменной энергии на поддержание составляет у жвачных в среднем 70 %, на образование молока — 60, на рост — 50, на откорм — 25–30 %.

Затраты энергии поддержания распределяются примерно поровну между функциями обеспечения (работа сердца, почек, легких, печени, ЦНС) и клеточными процессами (реосинтез белка, липидов, перемещение ионов через мембраны).

В накоплении энергии важную роль играет макроэргические соединения, в химических связях которых сосредоточено большое количество энергии. К таким соединениям относятся АТФ, АДФ, креатинфосфат и др. В них аккумулируется энергия белков, жиров и углеводов. Больше всего тепла образуется в мышцах, а также в печени, почках, железах и легких. Значительно повышает теплопродукцию низкая температура воздуха, мышечная работа. Высокая температура, состояние покоя, кастрация животных, подкожный жировой слой и густой волосяной покров снижают образование тепла.

Терморегуля́ция (греч. thermē тепло + лат. regulare упорядочивать)

совокупность физиологических реакций организма, обеспечивающих постоянство температуры тела. Принято считать, что Т. свойственна лишь гомойотермным животным (млекопитающие и птицы), организм которых обладает способностью поддерживать температуру внутренних областей тела на относительно постоянном и достаточно высоком уровне (около 37—38° у млекопитающих и 40—42° у птиц) независимо от изменений температуры окружающей среды. Тех животных, температура тела которых зависит от температуры среды, относят к пойкилотермным. У человека (рис.) в норме температура тела, точнее температура так называемого ядра тела (т.е. мозга, крови, внутренних органов), поддерживается на уровне порядка 37°. Физиологический предел колебаний не превышает 1,5°. Изменение температуры крови и внутренних органо

№14.

Теплопродукция - (теплообразование) - образование тепла в организме в процессе его жизнедеятельности. У высших животных и человека происходит главным образом в результате окислительных процессов, связанных с дыханием, пищеварением, работой мышц, и находится в прямой зависимости от их интенсивности. При напряженной мышечной работе теплопродукция может возрастать в 10 раз по сравнению с состоянием покоя. При охлаждении животного в его клетках увеличивается скорость гидролиза АТФ и в мышцы поступает дополнительная энергия. Возникающее при этом беспорядочное сокращение отдельных групп мышечных волокон мы называем дрожью. Кроме того, у животных взъерошиваются волосы(пилоэрекция),между волосами увеличивается воздушная прослойка, что приводит к уменьшению обмена теплотой между животным и средой(атавистическое явление «гусиной кожи» у человека).При повышении температуры среды в организме возникают процессы, приводящие в действии термопонижающие центры, в результате чего происходит расширение кровеносных сосудов, увеличение потоотделения, учащения дыхания.

Теплопродукция.

В любой тепловой машине часть энергии сгоревшего топлива превращается в теплоту (нагревание парового котла, цилиндра двигателя внутреннего сгорания и т.п.), а часть в другие формы энергии (упругую энергию сжатого пара, электрическую и пр.); после того, как совершается полезная работа, эта часть энергии также переходит в теплоту и рассеивается в окружающем пространстве, в результате чего энтропия системы возрастает. Живой организм в какой-то степени сходен с тепловой машиной: он также выделяет теплоту в окружающую среду, т.е. обладает свойством теплопродукции за счет энергии, полученной от продуктов питания (энергия выделяется при окислении пищевых продуктов – белков, жиров, углеводов) или от фотосинтеза, и, кроме того, выполняет различные виды работы: механическую, электрическую, химическую, осмотическую. При совершении работы могут происходить дальнейшие трансформации энергии, но в конечном счете все виды энергии превращаются в теплоту, которая выводится в окружающее пространство, а энтропия системы возрастает.

Перенос тепла в живых организмах.

Благодаря теплопродукции температура тела у теплокровных животных обладает удивительным постоянством и не зависит от температуры внешней среды. Лишь только при длительном и глубоком охлаждении температура тела может понижаться с одновременным значительным ослаблением всех функций организма.

Поскольку внешние условия, а также физиологические процессы могут меняться в определенных пределах, то для поддержания стационарного температурного состояния живые организмы в ходе эволюции выработали определенные механизмы, которые могут немного понижать или повышать температуру, увеличивая или уменьшая теплообмен с внешней средой.

При повышении температуры среды в организме возникают процессы, приводящие в действие термопонижающие центры, в результате чего происходит расширение кровеносных сосудов, увеличение потоотделения, учащение дыхания. Но наибольшая роль в этом процессе принадлежит переносу тепла кровью, обладающей большой теплоемкостью. Перенос тепла потоком крови аналогичен процессам в любом теплообменнике. Кровь выталкивается из левого желудочка сердца («двигатель»), проходит через «нагреватель» (ткани), через «радиатор» (поверхностные части тела, легкие), отдающий теплоту во внешнюю среду, и поступает обратно в сердце, в его правый желудочек.

№15

Для объяснения свойств вещества в газообразном состоянии используется модель идеального газа. Идеальным принято считать газ, если:

а) между молекулами отсутствуют силы притяжения, т. е. молекулы ведут себя как абсолютно упругие тела; б) газ очень разряжен, т.е. расстояние между молекулами намного больше размеров самих молекул; в) тепловое равновесие по всему объему достигается мгновенно. Условия, необходимые для того, чтобы реальный газ обрел свойства идеального, осуществляются при соответствующем разряжении реального газа. Некоторые газы даже при комнатной температуре и атмосферном давлении слабо отличаются от идеальных.

г) движение каждой молекулы подчиняется классическим законам динамики Ньютона.

Основными параметрами идеального газа являются давление, объем и температура.

Реальный разреженный газ приблизительно ведет себя как идеальный газ.

Одним из первых и важных успехов молекулярно-кинетической теории было качественное и количественное объяснение давления газа на стенки сосуда. Качественное объяснение заключается в том, что молекулы газа при столкновениях со стенками сосуда взаимодействуют с ними по законам механики как упругие тела и передают свои импульсы стенкам сосуда.

На основании использования основных положений молекулярно-кинетической теории было получено основное уравнение молекулярно-кинетической теории идеального газа, которое устанавливает связь между макроскопической величиной - давлением, которое может быть измерено, например манометром, и микроскопическими величинами, характеризующими молекулу:

где р - давление, m₀- масса молекулы, n - концентрация (число молекул в единице объема), v²- средний квадрат скорости молекул.

Если через Е обозначить среднюю кинетическую энергию поступательного движения молекулы

можно записать:

Давление идеального газа пропорционально концентрации молекул и средней кинетической энергии их поступательного движения.

16.Реальные газы.Уравнение состояния.

Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева.

Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Состояние реального газа часто на практике описывается обобщённым уравнением Менделеева — Клапейрона:

pV=Zr(p,T)*m/M*R*T

где p — давление; V - объем T — температура; Zr = Zr (p,T) — коэффициент сжимаемости газа; m - масса; М — молярная масса; R — газовая постоянная.

Уравнение состояния.

Для одного моля газа Ван-дер-Ваальса оно имеет вид:

(p+a/V2)(V-b)=RT

где

p — давление,

V — молярный объём,

T — абсолютная температура,

R — универсальная газовая постоянная.

Для ν молей газа Ван-дер-Ваальса уравнение состояния выглядит так

(p+av2/V2)(V/v-b)=RT

где v - объем.

P.S. ребята.формулу нормально не скинуть.так что пишу обозначение..

V2 - это значит большое V в квадрате.за какой буквой цифра стоит.значит та буква и в квадрате.))

a/V2 - черточка значит деление в столбик.что стоит первое то и на верху)

*- это умножение.

№17

На границе соприкосновения твердых тел с жидкостями наблюдаются явления смачивания, состоящие в искривлении свободной поверхности жидкости около твердой стенки сосуда. Поверхность жидкости, искривленная на границе с твердым телом, называется мениском. Линия, по которой мениск пересекается с твердым телом, называется периметром смачивания. Краевой угол θ служит мерой смачивания — это угол между плоскостью, касательной к поверхности жидкости, и стенкой (плоскостью поверхности твердого тела). Внутри краевого угла всегда находится жидкость.

Жидкость называется смачивающей твердое тело, если краевой угол острый 0 <О< 90 градусов (см.рис. а) Для жидкостей, не смачивающих твердое тел, краевой угол тупой: 90 <О< 180 (см. рис. б).

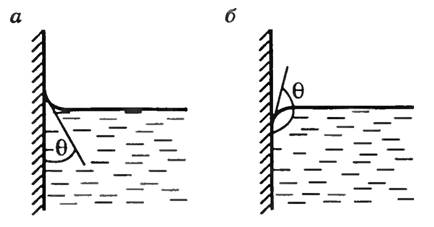
Искривление свободной поверхности жидкости наблюдается при смачивании, вблизи стенки сосуда. Степень искривления свободной поверхности характеризуется краевым углом.

Смачивание имеет важное значение как в быту, так и в промышленности. Хорошее смачивание необходимо при крашении, стирке, обработке фотоматериалов, нанесении лакокрасочных покрытий, при склеивании материалов, при пайке, во флотационных процессах (обогащение руд ценной породой).

И наоборот, при сооружении гидроизоляционных устройств необходимы материалы, не смачиваемые водой.

№18

Жидкость является агрегатным состоянием вещества, промежуточным между газооб­разным и твердым, поэтому она обладает свойствами как газообразных, так и твердых веществ.

Молекулы жидкости расположены почти вплотную друг к другу. Поэтому жидкости очень плохо сжимаются, но хорошо сохраняют свой объем. Молекулы жидкости совершают колебания около положения равновесия. Время от времени молекула совершает переходы из одного оседлого состояния в другое, как правило, в направлении действия внешней силы. Время оседлого состояния молекулы мало и с ростом температуры уменьшается, а время перехода молекулы в новое оседлое состояние еще меньше. Поэтому жидкости текучи, не сохраняют своей формы и принимают форму сосуда, в который налиты.

Основные свойства жидкости: текучесть, сохранение объёма, плотность жидкости, вязкость, смешиваемость, диффузия, смачивание, кипение, испарение и конденсация, поверхностное натяжение.

Проявление сил поверхностного натяжения связано с силами притяжения между молекулами и подвижностью молекул в жидкостях.

   Внутри жидкости силы притяжения, действующие на одну молекулу со стороны соседних с ней молекул, взаимно компенсируются. Любая молекула, находящаяся у поверхности жидкости, притягивается молекулами, находящимися внутри жидкости. Под действием этих сил молекулы с поверхности жидкости уходят внутрь жидкости, и число молекул, находящихся на поверхности, уменьшается до тех пор, пока свободная поверхность жидкости не достигнет минимального из возможных в данных условиях значения. Минимальную поверхность среди тел данного объема имеет шар, поэтому при отсутствии или пренебрежимо малом действии других сил жидкость под действием сил поверхностного натяжения принимает форму шара.

Силой поверхностного натяжения называют силу, которая действует вдоль поверхности жидкости перпендикулярно к линии, ограничивающей эту поверхность, и стремится сократить ее до минимума.

Отношение модуля силы поверхностного натяжения, действующей на границу поверхностного слоя длиной l, к этой длине есть величина постоянная, не зависящая от длины l. Эту величину называют коэффициентом поверхностного натяжения и обозначают греческой буквой «сигма»:

Коэффициент поверхностного натяжения выражается в ньютонах на метр (Н/м). Поверхностное натяжение различно у разных жидкостей.

№ 19

Искривление поверхности жидкости создает дополнительное (избыточное) давление на жидкость по сравнению с давлением под плоской поверхностью. Для сферической поверхности жидкости, при краевом угле, равном 0 или 180 дополнительной давление равно:

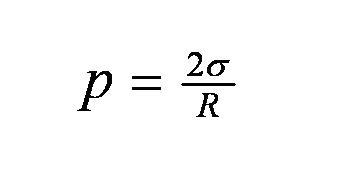где ф– коэффициент поверхностного натяжения, R – радиус сферической поверхности. Дополнительное давление внутри сферического пузыря радиуса R вызывается избыточным давлением на обеих поверхостях пузыря и равно  

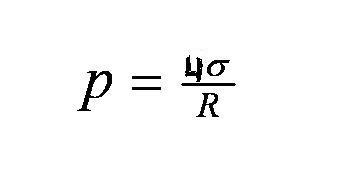
Формула Лапласа

Рассмотрим тонкую жидкую плёнку, толщиной которой можно пренебречь. Стремясь минимизировать свою свободную энергию, плёнка создаёт разность давления с разных сторон. Этим объясняется существование мыльных пузырей: плёнка сжимается до тех пор, пока давление внутри пузыря не будет превышать атмосферное на величину добавочного давления плёнки. Добавочное давление в точке поверхности зависит от средней кривизны в этой точке и даётся формулой Лапласа:

Здесь R_1,2 — радиусы главных кривизн в точке. Они имеют одинаковый знак, если соответствующие центры кривизны лежат по одну сторону от касательной плоскости в точке, и разный знак — если по разную сторону. Например, для сферы центры кривизны в любой точке поверхности совпадают с центром сферы, поэтому

R₁ = R₂ = R

Для случая поверхности кругового цилиндра радиуса R имеем

Из формулы Лапласа следует, что свободная мыльная плёнка, натянутая на рамку произвольной формы и не образующая пузырей, будет иметь среднюю кривизну, равную 0.

В природе принцип несмачиваемости и водонепроницаемости капилляров реализован и с успехом используется водоплавающими. Например, перья или мех представляют собой упорядоченную систему из множества капилляров, поэтому вода даже на глубине не проникает под перья или мех водоплавающих, а с поверхности перьев скатывается.

Капиллярные явления позволяют всасывать питательные элементы, кровообращение в живых организмах основано на капиллярном явлении.

Капиллярными явлениями называют подъем или опускание жидкости в трубках малого диаметра – капиллярах. Смачивающие жидкости поднимаются по капиллярам, не смачивающие – опускаются.

№20

Определение вязкости:

Между молекулами жидкости существуют силы взаимного притяжения, которые проявляются при движении одного слоя жидкости относительно другого в виде внутреннего трения или вязкости.

Закон Ньютона:

Ньютон показал, что сила F (сила вязкого трения), которую необходимо приложить, чтобы два смежных слоя скользили один по другому, пропорциональна площади поверхности слоев S и градиенту скорости между ними.

Таким образом, единица измерения вязкости в СИ – Па*с (паскаль*секунда). Такую вязкость имеет жидкость, в которой касательная сила в 1Н, действующая на слой площадью в 1м², поддерживает разность скоростей в 1м/с между двумя слоями, расстояние между которыми 1м.

Вязкость большинства жидкостей зависит только от их природы и от температуры; их называют Ньютоновскими, т.е. подчиняющимися закону Ньютона. К ним относят воду, водные растворы, этиловый спирт и т.д. Коэффициент вязкости других жидкостей зависит также от давления и градиента скорости. Такие жидкости называют неньютоновскими. К ним относят высокомолекулярные соединения, суспензии, например кровь. При движении крови по сосудам её форменные элементы концентрируются в центральной части потока, где вязкость из-за этого увеличивается. Так, при анемии относительная вязкость крови снижается до 2-3, а при полицитемии повышается до 10-15 и выше.

При течении вязкой жидкости часть механической энергии переходит во внутреннюю.

Течение вязкой жидкости по трубам.

Течение вязкой жидкости может быть ламинарным или турбулентным. Ламинарным называют такое течение жидкости, при котором отсутствует перемешивание соседних слоев потока. В турбулентном потоке скорости частиц жидкости в каждой его точке непрерывно меняются, приходят в колебательное движение, которое сопровождается появлением звука.

Скорость V_кр, при которой ламинарное течение переходит в турбулентное, называют критической скоростью и определяют её из числа Рейнольдца, характеризующего режим течения жидкости.

21 вопрос Твердые тела в обычных условиях сохраняют и объем и форму. Это объясняется тем, что притяжение между их частицами еще больше чем у жидкостей. Частицы (молекулы или атомы) большинства твердых тел расположены в определенном порядке. Такие твердые тела называются кристаллическими. Хотя частицы таких тел и движутся , это движение колеблется около определенных точек (положений равновесия). Частицы не могут далеко уйти от этих точек и тела сохраняют форму и объем. Механические свойства ТВЕРДОСТЬ Под твердостью понимают сопротивление материала, которое он создает при вдавливании или царапании его поверхности другим телом. МЯГКОСТЬ О мягкости материала говорят, когда его можно сжать с приложением небольшой силы или процарапать другим материалом. ВЯЗКОСТЬ (ТЯГУЧЕСТЬ) Под вязкостью понимают способность материала под воздействием изгибных, ударных и толчковых нагрузок хотя и поддаваться, но при этом не разрушаться. Вязкими являются такие материалы, как сталь, свинец, дерево, кожа и термопластичные пластмассы. Они в основном имеют волокнистое строение. ХРУПКОСТЬ Под хрупкостью понимают свойство материала под воздействием изгибающих, ударных и толчковых нагрузок не изменять свою форму, а сразу разрушаться. УПРУГОСТЬ Упругость — это свойство материала позволять себя сжимать или растягивать, а после снятия нагрузки — возвращаться к первоначальной форме. ПЛАСТИЧНОСТЬ Пластичностью называют свойство материалов под воздействием нагрузки изменять свою форму и сохранять эту новую форму после снятия нагрузки Закон Гука Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации

№22. тепловые свойства жидких и твердых тел. Термодинамические методы лечения в ветеринарии. Жидкость при постепенном повышении температуры и сохраняющемся внешнем давлении переходит из одного фазового состояния в другое лед-жидкость-пар. Твердые тела приповышении температуры плавление. Поддержание постоянной температупы тела связано с наличием центра терморегуляции в гипоталамусе.Температурными датчиками системы терморегуляции служат специальные рецепторы, находящиеся в коже и в некоторых слизистых оболочках. Если, например, поток теплоты из организма во внешнюю среду увеличивается, то возникает ощущение холода и происходят различные ответные реакции со стороны органов, которые могут быть расположены даже далеко от места раздражения. Кожа принимает основное участие в теплообмене (более 70% теплоотдачи). Воздействием на нее теплом/холодом можно влиять на теплообмен и на общий обмен веществ (терапевтическое значение). Местное нагревание в области сердца увеличивает число сердечных сокращений, что тонизирует сердечную мышцу. Так же обезбаливающее действие холода при воспалительных процессах. Для метода лечения путем теплопроводности применяют вещества, которые имеют большую пеплоемкость и относительно малую теплопроводность.

№23. Звук как физическое явление, характеристика звука. Звук представляет собой упругие волны, распространяющиеся в газообразных, жидких и твердых веществах с частотами от 0 до 10(в 13 степени) Гц. Характеристика звука: Звуковое(акустическое) давление - добавочное давление, образующееся в участках сгущения частиц в акустической волне. Затухание звука обусловлено тремя причинами: поглощением, рассеянием на неоднородностях среды и увеличением поверхности волнового фронта с расстоянием.

№24. Применение ультразвука в ветеринарии. Терапия: Терапевтическое действие ультразвука обусловлено механическим, тепловым и физико-химическим факторами. Их совместное действие увеличивает проницаемость клеточных мембран, расширяет кровеносные сосуды, улучшает обмен веществ. В ветеринарии широко используют ультразвук для лечения заболеваний суставов, сухожильного аппарата, мышечных атрофий, атонии преджелудочков КРС. Применяется фонофорез - введение с помощью ультразвука в ткани через поры кожи некоторых лекарственных средств. Под действием ультразвука увеличивается проницаемость клетточных мембран, что способствует проникновению в клетку лекарственных веществ.Есть два способа облучения: прямой и иммерсионный. Аутогемотерапия - внутримышечное или подкожное введение животному его собственной крови, взятой из вены.Такая операция способствует улучшению обменных процессов и стимуляции защитных сил организма.

25. Проводимость металлов. Закон Ома в дифференциальной форме.

1. Электрический ток в металлах связан только с одним видом носителей — свободными электронами. Особенностью сторения металлов является то, что значительная часть валентных электронов не принадлежат определённому атому.

При отсутствии приложенного к участку металлического проводника электрического поля электроны проводимости движутся хаотически и сталкиваются с узлами кристаллической решётки металла. При 0˚C скорость такого движения составляет ок. 10⁵ м/с.

При действии внешнего поля начинается направленный дрейф электронов от минуса к плюсу.

При нагревании металлического проводника хаотическое движение частиц проводника становится интенсивнее, что приводит к уменьшению направленной подвижности свободных электронов-носителей тока.

При низких температурах сопротивление скачком падает до нуля, т.е. наблюдается явление сверхпроводимости. Оно связано с тем, что в идеальной кристаллической решётке металла электроны перемещаются под действием электрического поля, взаимодействуя лишь с ионами, не находящимися в узлах решётки

2. Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Закон Ома в так называемой дифференциальной форме описывает исключительно электропроводящие свойства материала:

, где - сила тока; - удельная проводимость в-ва; – напряжённость поля.

№26.

В электролитах заряды появляются в жидкости за счет электролитической диссоциации молекул на ионы. Условно все вещества, растворенные в жидкости и частично диссоциирующие на ионы, делят на два типа: сильные электролиты и слабые. Сильные электролиты - вещества полностью диссоциирующие на ионы. Это соли типа NaCl, сильные кислоты типа HCl. Слабые электролиты - малодиссоциирующие вещества, т.е. они растворяются в виде молекул, только малая часть молекул диссоциирует на ионы. Пример - спирты, органические кислоты (например, уксусная кислота). Число ионов зависит от концентрации растворенных веществ. Подвижность ионов в электролитах невелика, обычно она составляет порядка 10-8 м2/(В•с). За счет большой растворяющей способности воды, обычно электропроводность влажных сред оказывается достаточно великой, т.к. растворенные вещества зачастую содержат сильно диссоциирущие соли. Причиной электропроводности увлажненных диэлектриков является растворение в воде различных примесей и их последующая диссоциация на ионы. Поэтому обычно самым большим “врагом” электрической изоляции является вода, попадание которой в диэлектрик ухудшает электрофизические характеристики материала. Сопротивление R зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем: J=σE j — вектор плотности тока, σ — удельная проводимость, E — вектор напряжённости электрического поля.

№27.

Разряд , существующий только при действии внешнего ионизатора, называется несамостоятельным разрядом . Если ионы, необходимые для поддержания электропроводимости газа, создается самим разрядом (в результате процессов происходящих в разряде), такой газовый разряд называется самостоятельным . Несамостоятельный газовый разряд - если действие ионизатора прекратить , то прекратится и разряд . Когда разряд достигает насыщения - график становится горизонтальным. Здесь электропроводность газа вызвана лишь действием ионизатора. Самостоятельный газовый разряд - в этом случае газовый разряд продолжается и после прекращения действия внешнего ионизатора за счет ионов и электронов, возникших в результате ударной ионизации ( = ионизации эл. удара); возникает при увеличении разности потенциалов между электродами ( возникает электронная лавина). Несамостоятельный газовый разряд может переходить в самостоятельный газовый разряд при Ua = Uзажигания. Электрический пробой газа- процесс перехода несамостоятельного газового разряда в самостоятельный . Самостоятельный газовый разряд бывает 4-х типов: 1. тлеющий - при низких давлениях(до нескольких мм рт.ст.) -наблюдается в газосветных трубках и газовых лазерах. 2. искровой - при нормальном давлении и высокой напряженности электрического поля (молния - сила тока до сотен тысяч ампер). 3. коронный - при нормальном давлении в неоднородном электрическом поле ( на острие ). 4. дуговой - большая плотность тока, малое напряжение между электродами ( температура газа в канале дуги -5000-6000 градусов Цельсия); наблюдается в прожекторах, проекционной киноаппаратуре. Вольтамперная характеристика - зависимость напряжения от тока или тока от напряжения на участке электрической цепи. В. х. может изображаться аналитически — как функция V = f (I), где V — напряжение, I — ток; графически — в виде линии в системе координат (V, I), например, анодная характеристика электровакуумных ламп.

28

Магнитное поле - это особый вид материи, специфической особенностью которой является действие на движущийся электрический заряд, проводники с током, тела, обладающие магнитным моментом, с силой, зависящей от вектора скорости заряда, направления силы тока в проводнике и от направления магнитного момента тела.

Характеристики магнитных полей:

Напряжённость магнитного поля (А/м).

Магнитная индукция (тесла, Те).

Магнитный поток (вебер, Вб).

Сила намагничивания – произведение силы тока (А) на число витков.

Рассеянное магнитное поле быстро уменьшается по мере его удаления от источника, поэтому магнитные поля имеют большие градиенты.

Однородность магнитного поля.

Способность магнитных силовых линий концентрироваться в ферромагнитных веществах.

Закон Био – Свара – Лапласа – это закон, который позволяет определить модуль вектора магнитной индукции в произвольно выбранной точке магнитного поля, созданного постоянным электрическим током на определенном участке.

Закон Био – Свара – Лапласа звучит так: если постоянный ток проходит по контуру, который находится в вакууме, rо – точка, в которой ищется поле, то индукция магнитного поля в этой точке будет выражено интегралом:

далее в документе формула.

вопрос №29 Закон Ампера устанавливает, что на проводник с током, помещенный в однородное магнитное поле, индукция которого В, действует сила, пропорциональная силе тока и индукции магнитного поля: F = BIlsina (a - угол между направлением тока и индукцией магнитного поля ). Эта формула закона Ампера оказывается справедливой для прямолинейного проводника и однородного поля. Если проводник имеет произвольную формулу и поле неоднородно, то Закон Ампера принимает вид: dF = I*B*dlsina Закон Ампера в векторной форме: dF = I [dl B] Сила Ампера направлена перпендикулярно плоскости, в которой лежат векторы dl и B. Для определения направления силы, действующей на проводник с током, помещенный в магнитное поле, применяется правило левой руки. Вектор магнитной индукции - это основная силовая характеристика магнитного поля . Пробный контур, помещенный в магнитное поле, испытывает со стороны магнитного поля действие вращающего момента сил . Единица измерения магнитной индукции в системе СИ: Единица измерения магнитной индукции в системе СИ:

  Взаимосвязь между вектором магнитной индукции  и напряженностью поля :

     

вопрос №29

Закон Ампера устанавливает, что на проводник с током, помещенный в однородное магнитное поле, индукция которого В, действует сила, пропорциональная силе тока и индукции магнитного поля:

F = BIlsina (a - угол между направлением тока и индукцией магнитного поля ). Эта формула закона Ампера оказывается справедливой для прямолинейного проводника и однородного поля.

Если проводник имеет произвольную формулу и поле неоднородно, то Закон Ампера принимает вид:

dF = I*B*dlsina

Закон Ампера в векторной форме:

dF = I [dl B]

Сила Ампера направлена перпендикулярно плоскости, в которой лежат векторы dl и B.

Для определения направления силы, действующей на проводник с током, помещенный в магнитное поле, применяется правило левой руки.

Вектор магнитной индукции - это основная силовая характеристика магнитного поля . Пробный контур, помещенный в магнитное поле, испытывает со стороны магнитного поля действие вращающего момента сил .

Единица измерения магнитной индукции в системе СИ:см.документ.

30

магнитные св-ва вещества и теорию ампера см.документ.

Магнитный момент, основная величина, характеризующая магнитные свойства вещества. Источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макрои микротоки. Элементарным источником магнетизма считают замкнутый ток. Из опыта и классической теории электромагнитного поля следует, что магнитные действия замкнутого тока (контура с током) определены, если известно произведение (М) силы тока i на площадь контура s (М = i s/c в СГС системе единиц, с — скорость света). Вектор М и есть, по определению, Магнитный момент Его можно записать и в иной форме: М = m l, где m — эквивалентный магнитный заряд контура, а l — расстояние между «зарядами» противоположных знаков (+ и -).

№31 вопрос

Вектор намагничивания —магнтный момент элементарного объёма, используемый для описания магнитного состояния вещества.

Магнитная восприимчивость —физическая величина, характеризующая связь между магнитным моментом (намагниченностью) вещества и магнитным полем в этом веществе.

Магнитная проницаемость — физическая величина, характеризующая связь между магнитной индукцией B и напряженностью магнитного поля H в веществе.

вопрос 32 Диамагнетиками называются вещества, молекулы которых не обладают собственным магнитным моментом. Под действием внешнего магнитного поля в атомах и молекулах наводится (индуцируется) магнитный момент, направленный противоположно вектору индукции внешнего поля. Такое направление индуцированного магнитного момента приводит к тому, что диамагнетики выталкиваются из магнитного поля. К диамагнетикам относятся все цветные металлы (медь, алюминий, серебро, золото и т.д.), инертные газы (неон, аргон, гелий, криптон,), органические стекла. В магнитном поле диамагнитные вещества легко распознаются без всяких измерений. Они всегда вытесняются из областей высокой напряженности магнитного поля. Диамагнитный эффект является проявлением закона электромагнитной индукции на атомном уровне. Электронную орбиту можно рассматривать как замкнутый контур. Изменение внешнего магнитного поля, пересекающего электрический контур, индуцирует в нем ток такого направления, магнитное поле которого будет противодействовать внешнему изменению. Поэтому при помещении диамагнетика в магнитное поле происходит как бы «экранирование» внешнего магнитного поля возникающим внутренним полем, направленным противоположно внешнему. Противодействие внешнему полю выражается в некотором торможении угловой скорости орбитального движения электронов. Магнитное поле вызывает прецессию орбиты вокруг направления поля, что вызывает появление добавочного момента, направленного против поля.