Основные понятия

Обозначим метрическое пространство через .

Определение: Последовательность , принадлежащая метрическому пространству, называется фундаментальной, если каждому соответствует номер такой, что для любых справедливо неравенство .

Определение: Последовательность , принадлежащая метрическому пространству , называется сходящейся, если существует такой, что каждому соответствует номер такой, что для всех справедливо неравенство . Тогда называется пределом последовательности.

Теорема: Если последовательность имеет предел, то он единственный.

Доказательство.

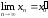Действительно, если и , то . Так как и , то , т.е. .

Теорема доказана.

Определение: Полным метрическим пространством называется метрическое пространство, в котором каждая фундаментальная последовательность сходится.

Теорема: Метрика как функция двух аргументов является непрерывной функцией, т.е. если и , то .

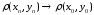Доказательство:

Пусть , , , .

По неравенству треугольника:

(1)

и

. (2)

Из (1) получаем:

.

Из (2) получаем:

.

.

Так как ,

так как

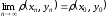
ч.т.д.

Обозначим .

В метрическом пространстве можно рассматривать различные множества, окрестности точек, предельные точки и другие понятия классического анализа.

Определение: Под окрестностью точки понимают множество, содержащие открытый шар радиуса с центром в точке , т.е.

.

Определение: Точка называется предельной точкой для множества , если в любой окрестности точки содержится хотя бы одна точка из , отличная от .

Определение: Точка называется внутренней точкой множества , если она входит в вместе с некоторой своей окрестностью .

Определение: Множество называется открытым, если оно состоит из одних внутренних точек. Множество называется замкнутым в себе, если оно содержит все свои предельные точки.

Метрическое пространство является замкнутым.

Подпространства могут быть и не замкнутыми подмножествами .

Если к присоединить все его предельные точки, то получаем замыкание .

Определение: Множество , лежащее в метрическом пространстве называется замкнутым, если оно совпадает со своим замыканием: .

- замкнутое множество, есть наименьшее замкнутое множество, содержащие .

Определение: Пусть . Множество называется плотным в , если . Множество называется всюду плотным, если . Множество называется нигде не плотным в , если каков бы ни был шар , найдется другой шар , свободный от точек множества .

Определение: Пространство называется сепарабельным, если в нем существует всюду плотное счетное множество.

В математическом анализе важную роль играет свойство полноты числовой прямой, то есть тот факт, что всякая фундаментальная последовательность действительных чисел сходится к некоторому пределу (Критерий сходимости Коши).

Числовая прямая служит примером полным метрических пространств.

Пространства изолированных точек, , , , , , являются полными метрическими пространствами.

Пространство не полно.

В анализе широко используется так называемая лемма о вложенных отрезках:

Пусть - система вложенных отрезков. Тогда для отрезка имеем .

Это значит, что все отрезки из множества имеют общую точку .

В теории метрических пространств аналогичную роль играет теорема о вложенных шарах.

Теорема: Для того, чтобы метрическое пространство было полным необходимо и достаточно, чтобы в нем всякая последовательность вложенных друг в друга шаров, радиусы которых , имела непустое пересечение.

Доказательство:

Необходимость:

Пусть - полное метрическое пространство и пусть - последовательность вложенных друг в друга замкнутых шаров.

Пусть - радиус, а - центр шара .

Последовательность центров - фундаментальна, так как при , а при . Так как - полно, то . Положим , тогда . Действительно, шар содержит все точки последовательности , за исключением, быть может точек . Таким образом точка является точкой прикосновения (предельной точкой) для каждого шара . Но так как - замкнутое множество, то .

Достаточность:

Пусть - фундаментальная последовательность. Докажем, что она имеет предел. В силу фундаментальности можем выбрать такую точку 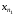последовательности, что при всех . Примем точку за центр замкнутого шара радиуса .Обозначим этот шар .

Выберем затем из так, чтобы любой при любом . Примем точку за центр шара радиуса и обозначим этот шар .

Если уже выбраны , то выберем так, чтобы и при всех и окружим его замкнутым шаров радиуса . Продолжая это построение, получим последовательность шаров , вложенных друг в друга, причем шар имеет радиус . Эта последовательность шаров имеет, по предположению, общую точку, обозначим её .

служит пределом последовательности . Но если фундаментальная последовательность содержит сходящуюся к подпоследовательность, то она сама сходится к тому же пределу, таким образом .

ч.т.д.

Теорема (Бэр): Полное метрическое пространство не может быть представлено в виде объединения счетного числа нигде не плотных множеств.

Доказательство:

Докажем от противного.

Пусть , где каждое из нигде не плотно. Пусть - некоторый замкнутый шар радиуса . Поскольку множество , будучи нигде не плотным, не плотно в , существует замкнутый шар радиуса , такой, что и .

Так как не плотно в , то в содержится замкнутый шар радиуса и т.д.

Получаем последовательность вложенных друг в друга замкнутых шаров , радиусы которых , причем . В силу теоремы о вложенных шарах пересечение 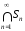содержит некоторую точку , которая по построению не принадлежит ни одному из множеств и , то есть противоречие, ч.т.д

В частности, всякое полное метрическое пространство без изолированных точек несчетно.

Действительно, в таком пространстве каждое множество, содержащее лишь одну точку, нигде не плотно.

Если пространство не полно, то его всегда можно включить некоторым единственным способом в полное пространство.

Определение: Пусть - метрическое пространство. Полное метрическое пространство называется пополнением пространства , если:

1) является подпространством пространства ,

2) всюду плотно в , то есть .

Например, пространство всех действительных чисел является пополнением пространства рациональных чисел.

Теорема: Каждое метрическое пространство имеет пополнение, и это пополнение единственно с точностью до изометрии, оставляющей неподвижными точки из .