
Метрические пространства
1. Определение. Основные примеры метрических пространств
Определение:
Метрическим
пространством
называется пара
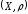 ,
где
,
где
 – некоторое множество и
– некоторое множество и
 –вещественная функция, удовлетворяющая
для всех
–вещественная функция, удовлетворяющая
для всех
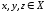 следующим аксиомам:
следующим аксиомам:
А1.
 и
и


 ;
;
А2.
 (аксиома симметрии);
(аксиома симметрии);
А3.
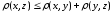 (аксиома треугольника).
(аксиома треугольника).
Определение:
Функция
 называется расстоянием
или
называется расстоянием
или
метрикой
на
 .
.
Если множество
 наделить другой метрикой
наделить другой метрикой
 ,
то получим другое метрическое пространство.
,
то получим другое метрическое пространство.
Примеры метрических пространств
1. Пространство изолированных точек.
Произвольное
множество
 и
и

2. Множество
действительных чисел с расстоянием
 образует метрическое пространство
образует метрическое пространство
 .
.
3. Множество
упорядоченных групп из
 действительных чисел
действительных чисел
 с
с
 называется
называется
 – мерным арифметическим евклидовым
пространством
– мерным арифметическим евклидовым
пространством
 .
.
Доказательство.
Для того, чтобы доказать, что пространство является метрическим, необходимо проверить выполнимость аксиом.
Пусть
 ,
,
 ,
,
 .
.
А1.
 и
и


 ,
,
 ,
…,
,
…,
 ,
т. е.
,
т. е.
 .
.
А2.


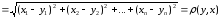 .
.
А3. Проверим,
выполняется ли в
 аксиома треугольника. Запишем аксиому
в виде:
аксиома треугольника. Запишем аксиому
в виде:
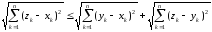 .
.
Полагая
 ,
,
 ,
получим
,
получим
 и
и
 .
.
Для доказательства
этого неравенства используется
неравенство Коши–Буняковского
 .
.
Действительно,

 ,
,
т.е.
 .
.
Следовательно, аксиома треугольника выполнена, и рассматриваемое множество с заданной метрикой является метрическим пространством.
Что и требовалось доказать.
4. Множество
упорядоченных групп из
 действительных чисел
действительных чисел
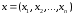 с
с
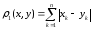 .
Это метрическое пространство обозначается
.
Это метрическое пространство обозначается
 .
.
5. Множество упорядоченных групп из действительных чисел с . Это метрическое пространство обозначается .
Примеры 3, 4 и 5 показывают, что один и тот же запас точек может быть по-разному метризован.
6. Множество
 всех непрерывных действительных функций,
определенных на сегменте
всех непрерывных действительных функций,
определенных на сегменте
 с расстоянием
с расстоянием
 .
Обозначают это метрическое пространство
как и само множество точек пространства:
.
Обозначают это метрическое пространство
как и само множество точек пространства:
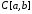 .
В частности, вместо
.
В частности, вместо
 пишут
пишут
 .
.
7. Через
 обозначается метрическое пространство,
точками которого служат всевозможные
последовательности
обозначается метрическое пространство,
точками которого служат всевозможные
последовательности
 действительных чисел, удовлетворяющие
условию
действительных чисел, удовлетворяющие
условию
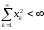 ,
и метрика определяется формулой
,
и метрика определяется формулой
 .
.
Доказательство.
Так как
 ,
то
,
то
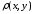 имеет смысл при всех
имеет смысл при всех
 .
Т.е. ряд
.
Т.е. ряд
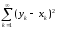 сходится, если
сходится, если
 и
и
 .
.
Покажем, что
 удовлетворяет аксиомам.
удовлетворяет аксиомам.
Аксиомы 1, 2 очевидны. Аксиома треугольника примет вид:
 .
.
Все ряды являются сходящимися.
Неравенство
справедливо для любого
 (см. пример 3). При
(см. пример 3). При
 получаем неравенство для
получаем неравенство для
 .
.
Что и требовалось доказать.
8. Рассмотрим
совокупность всех функций, непрерывных
на отрезке
 и
и
 .
Такое метрическое пространство
обозначается
.
Такое метрическое пространство
обозначается
 и называется пространством непрерывных
функций с квадратичной метрикой.
и называется пространством непрерывных
функций с квадратичной метрикой.
9. Рассмотрим
множество всех ограниченных
последовательностей
 действительных чисел. Определим
действительных чисел. Определим
 .
Это метрическое пространство обозначается
.
Это метрическое пространство обозначается
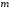 .
.
10. Множество
упорядоченных групп из
 действительных
чисел с расстоянием
действительных
чисел с расстоянием
 ,
где
,
где
 – любое фиксированное число
– любое фиксированное число
 ,
представляет собой метрическое
пространство, обозначаемое
,
представляет собой метрическое
пространство, обозначаемое
 .
.
Рассмотренная в
этом примере метрика
 превращается в евклидову метрику при
превращается в евклидову метрику при
 (см. пример 3) и в метрику примера 4 при
(см. пример 3) и в метрику примера 4 при
 .
Можно показать, что метрика
.
Можно показать, что метрика
 (см. пример 5) является предельным случаем
(см. пример 5) является предельным случаем
 .
.
11. Рассмотрим
всевозможные последовательности
 действительных чисел, удовлетворяющие
условию
действительных чисел, удовлетворяющие
условию
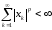 ,
где
,
где
 – некоторое фиксированное число, а
расстояние определяется формулой
– некоторое фиксированное число, а
расстояние определяется формулой
 .
Имеем метрическое пространство
.
Имеем метрическое пространство
 .
.
12. Пусть
 – множество всех бесконечных
последовательностей –комплексных
чисел
– множество всех бесконечных
последовательностей –комплексных
чисел
 .
Определим
.
Определим
 .
Имеем метрическое пространство.
.
Имеем метрическое пространство.
Определение:
Пусть
 – метрическое пространство и
– метрическое пространство и
 – любое подмножество
– любое подмножество
 .
Тогда
.
Тогда
 с той же функцией
с той же функцией
 ,
которая теперь определена для
,
которая теперь определена для
 ,
представляет собой метрическое
пространство, которое называется
подпространством
пространства
,
представляет собой метрическое
пространство, которое называется
подпространством
пространства
 .
.
