Министерство образования РФ

Московский государственный институт электроники и математики (Технический университет)

КАФЕДРА "ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА"

Методические указания

по выполнению лабораторной работы №4

“Закраска поверхностей”

по курсу

"Компьютерная графика"

Москва, 1999 г.

Изучение различных способов закраски поверхностей.

Методические указания к лабораторной работе № 4 “Закраска поверхностей” являются учебно-методическим материалом по дисциплине “Компьютерная графика”, изучаемой студентами 3 курса специальности “Вычислительные машины, комплексы, системы и сети”.

Лабораторная работа выполняется в объеме 4-6 часов.

Основным содержанием работы является изучение различных методов закраски поверхностей для решения различных графических анимационных задач.

1. Цель работы.

Целью данной лабораторной работы является изучение основных методов закрашивания поверхностей, а именно методов:

1. Однотонной закраски граней многогранника;

2. Закраски поверхности методом Гуро;

3. Закраски поверхности методом Фонга.

2. Теоретическая часть

2.1. Общие сведения

Как известно, световая энергия, падающая на поверхность от источника света, может быть отражена, поглощена или пропущена. Распределение этой энергии зависит от длины световой волны и свойств поверхности. Цвет поверхности определяется поглощаемыми длинами волн, однако для закрашивания объекта используется оценка отражённого света. Чем интенсивность отражённого света выше, тем выше должна быть интенсивность цвета пикселя при закраске. Свет, отражённый от объекта, может быть диффузным или зеркальным.

2.2. Простая модель освещенности.

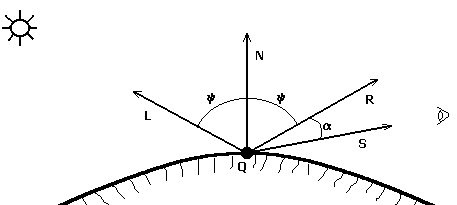
Световая энергия, падающая на поверхность, может быть поглощена, отражена или пропущена. Частично она поглощается и превращается в тепло, а частично отражается или пропускается. Объект можно увидеть, только если он отражает или пропускает свет; если же объект поглощает весь падающий свет, то он невидим и называется абсолютно черным телом. Свойства отраженного света зависят от строения, направления и формы источника света, от ориентации и свойств поверхности. Отраженный от объекта свет может также быть диффузным или зеркальным. Диффузное отражение света происходит, когда свет как бы проникает под поверхность объекта, поглощается, а затем вновь испускается. При этом положение наблюдателя не имеет значения, так как диффузно отраженный свет рассеивается равномерно по всем направлениям. Зеркальное отражение происходит от внешней поверхности объекта.

L – вектор направления источника света.

N – нормаль к поверхности в точке Q.

R – отраженный луч.

S – вектор наблюдения.

С учетом различных законов и свойств ( более подробно см. Д.Роджерс “Алгоритмические основы компьютерной графики” ) получим формулу для вычисления интенсивности света в точке Q.

N,L,R,S – единичные векторы, берется их скалярное произведение

Ia – интенсивность рассеяного света. Il – интенсивность точечного источника.

Ka – коэффициент диффузного отраженного света. (0 Ka 1)

Kd – коэффициент диффузного отражения. (0 Kd 1)

Ks – коэффициент зеркального отражения. K – произвольная постоянная.

D – определяется положением ближайшего объекта к точке наблюдения, т.е. ближайший объект освещается с полной интенсивностью, а более далекие – с уменьшенной.

n – степень, аппроксимирующая пространственное распределение зеркально отраженного света.

2.3. Определение нормали к поверхности.

Во многих алгоритмах удаления невидимых линий и поверхностей используются только ребра или вершины, поэтому, для того чтобы объединить их с моделью освещения, необходимо знать приближенное значение нормали на ребрах и в вершинах. Пусть заданы уравнения плоскостей полигональных граней, тогда нормаль к их общей вершине равна среднему значению нормалей ко всем многоугольникам, сходящимся в этой вершине. Например.

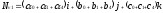
где a0a1a4b0b1b4c0c1c4 – коэффициенты уравнений плоскостей трех многоугольников P0,P1,P4, окружающих V1. Соответсвенно единичная нормаль равна: Nv1 / |Nv1|

Если же уравнения плоскостей не заданы, то нормаль к вершине можно определить, усредняя векторные произведения всех ребер, пересекающихся в вершине. Еще раз для вершины V1 имеем:

Соответсвенно единичная нормаль равна: Nv1 / |Nv1|

Обратите внимание на то, что полученные нормали, высчитанные двумя способами, различаются как по величине, так и по направлению. Поэтому модель освещения дает несколько отличающиеся результаты, в зависимости от использованного метода аппроксимации.

2.4. Определение вектора отражения.

Для модели освещенности чрезвычайно важно правильно задавать направление векторов отражения. В данном разделе рассмотрим несколько наиболее общих методов. По закону отражения вектор падающего света, нормаль к поверхности и вектор отражения лежат в одной плоскости, причем на этой плоскости угол падения равен углу отражения. Фонг вывел отсюда простое решение для случая, когда свет падает вдоль оси Z. Это предположение удобно для модели освещения с одним точечным источником. Если начало системы координат перенести в точку поверхности, то проекция нормали и вектора отражения на плоскость XY будут лежать на одной прямой. Таким образом компоненты единичных векторов N и R следующим образом.

Rz = 2*Nz*Nz – 1; Rx = 2*Nz*Ny; Ry = 2*Nz*Nx;

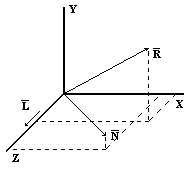
Когда свет падает не по оси Z ( например, когда источников света несколько ), таким методом пользоваться нельзя. Можно перенести и повернуть каждый источник так, чтобы свет падал вдоль оси Z; однако проще перенести и повернуть нормаль так, чтобы она была параллельна оси Z, а точку P поверхности принять за начало координат. Тогда плоскость XY будет касательной к поверхности, а x- и y-составляющие единичных векторов падения и отражения будут иметь разные знаки; z-составляющие этих векторов, будут, конечно, равны. Для того, чтобы получить результаты в первоначальной ориентации, надо выполнить обратное преобразование. В перемещенной и повернутой системе координат: Rx = -Lx; Ry = -Ly; Rz = Lz.

И наконец общий метод. В нем условие того, что единичная нормаль, единичный метод падения и единичный вектор отражения лежат в одной плоскости, записывается при помощи их векторных произведений. Равенство углов падения и отражения выражается через скалярное произведение этих векторов.

Из этой системы и находим компоненты вектора R.

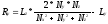
2.5. Однотонная закраска граней многогранника

Этот простейший способ закраски заключается в том, что на каждой из граней выбирается по одной точке, для неё определяется освещённость, а затем вся грань закрашивается с найденной освещённостью.

Предложенный алгоритм обладает, однако, одним большим недостатком – полученное изображение имеет неестественный многогранный вид. Это объясняется тем, что определяемая подобным образом освещенность сцены не является непрерывной величиной, а имеет кусочно-постоянный характер.

Однако данный метод является самым быстрым.

2.6. Закраска методом Гуро

Достаточно простым методом закраски поверхностей является метод Гуро, который основывается на определении освещенности грани в ее вершинах с последующей билинейной интерполяцией получившихся величин на всю грань.

Обратимся к рисунку, на котором изображена выпуклая четырехугольная грань.

Предположим, что интенсивности в ее вершинах V₁, V_2, V_3, V₄ известны и равны I_v1, I_v2, I_v3 и I_v4.

Пусть W – произвольная точка грани. Для определения интенсивности (освещенности) в этой точке проведем через нее горизонтальную прямую. Обозначим через U и V точки пересечения проведенной прямой с границей грани.

Будем считать, что интенсивность на отрезке UV изменяется линейно, то есть

I_W = (1 - t)I_U – tI_V ,

где t = UW/UV, 0 t 1

Для определения интенсивности в точках U и V вновь воспользуемся линейной интерполяцией, также считая, что вдоль каждого из ребер границы интенсивность изменяется линейно.

Тогда интенсивность в точках U и V вычисляется по формулам:

I_U = (1 - u)I_V4 – uI_{V1 ,}

I_V = (1 - v)I_V1 – vI_{V2 ,}

где u = V₄U/ V₄ V₁, 0 u 1, v = V₁V/ V₁ V₂, 0 v 1 .

Метод Гуро обеспечивает непрерывное изменение интенсивности при переходе от одной грани к другой без разрывов и скачков.

Еще одним преимуществом этого метода является его инкрементальный характер: грань рисуется в виде набора горизонтальных отрезков, причем так, что интенсивность последующего пиксела отрезка отличается от интенсивности предыдущего на величину постоянную для данного отрезка. Кроме того, при переходе от отрезка к отрезку значения интенсивности в его концах также изменяются линейно.

Таким образом, процесс рисования грани слагается из следующих шагов:

1. Проектирование вершин грани на экран;

2. Отыскание интенсивностей в вершинах по формуле: I = I_a k_a + (I₁k_d / d + k)cos , где: I_a - интенсивность рассеяного света;

k_a – (постоянный) коэффициент диффузного отражения рассеяного света, 0k_a1;

I₁ – интенсивность точечного источника;

k_d – коэффициент диффузного отражения (постоянная величина, 0 k_d 1);

d – произвольная постоянная;

- угол между направлением на источник света и (внешней) нормалью к поверхности.

3. Определение координат концов очередного отрезка и значений интенсивности в них линейной интерполяцией;

4. Рисование отрезка с линейным изменением интенсивности между его концами.

Замечания:

1. При определении освещенности в вершине, естественно, встает вопрос о выборе нормали. В качестве нормали в вершине выбирается нормированная сумма нормалей прилегающих граней

n = (a₁n₁ + …+ a_kn_k)/ a₁n₁ + …+ a_kn_k , где a₁n₁ + …+ a_kn_k – произвольные весовые коэффициенты.

2. Дефекты изображения, возникающие при закраске Гуро, частично объясняются тем, что этот метод не обеспечивает гладкости изменения интенсивности.

2.7 Закраска методом Фонга

Закраска Фонга требует больших вычислительных затрат, однако она позволяет разрешить многие проблемы метода Гуро. При закраске Фонга вдоль сканирующей строки интерполируется вектор нормали, который затем испльзуется в модели освещения для вычисленя интенсивности пикселя. При этом достигается лучшая локальная аппроксимация кривизны поверхности и, следовательно, получается более реалистичное изображение. В частности, правдоподобнее выглядят зеркальные блики. Это объясняется тем, что при расчете освешенности используется не только рассеянный свет и диффузное отражение (как в методе Гуро), но и отраженный свет (зеркальное отражение):

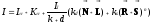
При закраске Фонга аппроксимация кривизны поверхности производится сначала в вершинах многоугольников путем аппроксимации нормали в вершине. После этого билинейной интерполяцией вычисляется нормаль в каждом пикселе. Например:

Ищем нормаль в точке Q линейной интерполяцией между A и B, в R – между B и C, и , наконец, в P – между Q и R. Таким образом:

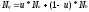
, где U = AQ / AB, W = BR / BC, T = QP / QR.

Хотя метод Фонга устраняет большинство недостатков метода Гуро, он тоже основывается на линейной интерполяции. Поэтому в местах разрыва первой производной интенсивности заметен эффект полос Маха, хотя и не такой сильной, как при закраске Гуро. Кроме того, закраска может значительно изменяться от кадра к кадру. Это происходит из-за того, что правило закраски зависит от поворотов, а обработка ведется в пространстве изображения. Поэтому, когда от кадра к кадру меняется ориентация объекта, его закраска тоже изменяется, причем достаточно заметно.