
- •Вопросы к зачету по высшей математике для юристов
- •Изобразите данные графически
- •Найдите коэффициент корреляции
- •Постройте эмпирическую ломаную регрессии
- •Изобразите данные графически
- •Найдите коэффициент корреляции
- •Постройте эмпирическую ломаную регрессии
- •Изобразите данные графически
- •Найдите коэффициент корреляции
- •Постройте эмпирическую ломаную регрессии
- •9. По сведениям автоинспекции, количество дорожных происшествий на улицах города в сентябре было таким:
- •9. Увд города опубликовало сводку о числе правонарушений, совершенных подростками за первые 20 дней сентября:
- •9.Средняя месячная зарплата за год каждого из десяти случайно отобранных работников хозяйства такова:
- •Изобразите данные графически
- •Найдите коэффициент корреляции
- •Постройте эмпирическую ломаную регрессии
- •9. По сведениям автоинспекции, количество дорожных происшествий на улицах города в сентябре было таким:
- •Изобразите данные графически
- •Найдите коэффициент корреляции
- •Постройте эмпирическую ломаную регрессии
- •5.Студенты одной группы должны сдать 5 экзаменов в течение десяти дней. Сколькими способами можно составить расписание экзаменов, если в один день разрешается сдавать не более одного экзамена.
-
Изобразите данные графически
-
Найдите коэффициент корреляции
-
Постройте эмпирическую ломаную регрессии
-
Определите параметры эмпирической линейной регрессии y=kx+b
Контрольная работа по высшей математике для юристов
Вариант 5.
-
Изобразить на диаграмме Эйлера- Венна:
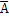 ∩
(В
U
С)
∩
(В
U
С)
2. Найти 1) производную функции у=х3 ctg х +еcos x
2) предел
limx→3![]()
-
Найти промежутки выпуклости графика функции: у=4х3+6х2+7х-12
-
Найти площадь фигуры ограниченной линиями у=х2-5х+б, у=0.
-
В студенческой группе (12 девушек и 10 юношей) разыгрываются 7 билетов в кино. Сколько существует различных вариантов.
6.Ведутся поиски 3 преступников. Каждый из них независимо от других может быть обнаружен в течение суток с вероятностью 0,7. Какова вероятность того, что в течение суток будет обнаружен только один преступник.
7. Ящик содержит 14 деталей, среди которых 5 бракованных. Найти вероятность того, что наудачу отобранных 5 деталях окажется 2 бракованные детали.
8. Даны точки
А(-4,3,-б) В(3,-1,5) С(0,4,-5) Найти (2![]() -
-
![]() ).
).
![]() ,
длину
,
длину
![]() и угол
АВС
и угол
АВС
9. По сведениям автоинспекции, количество дорожных происшествий на улицах города в сентябре было таким:
10 7 8 7 8 11 10 8 7 11 6 5 7 8 7 10 9 7 12 7 8 8 6 8 11 10 9 9 8 7.
Найти статистическое распределение выборки. Найти выборочную среднюю, дисперсию, среднее квадратическое отклонение.
10. Майор Зимин решил сравнить среднее число книг, прочитанных среднестатистическим восьмиклассником за год, с количеством правонарушений, совершенных подростками в его микрорайоне в течение года. Проанализировав данные за 10 лет, он получил следующую таблицу
|
X |
18 |
24 |
20 |
22 |
18 |
38 |
39 |
30 |
35 |
38 |
|
Y |
20 |
20 |
15 |
15 |
14 |
4 |
6 |
10 |
8 |
5 |
Здесь Х-среднее число книг прочитанных одним восьмиклассником за год, У-число правонарушений в течении года.
-
Изобразите данные графически
-
Найдите коэффициент корреляции
-
Постройте эмпирическую ломаную регрессии
-
Определите параметры эмпирической линейной регрессии y=kx+b
Контрольная работа по высшей математике для юристов.
Вариант 6
-
Изобразить на диаграмме Эйлера-Венна:
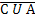 ∩ В
∩ В
-
2 Найти 1) производную функции y=x5arccosx – ctg ln х
2) предел ![]()
3. Найти промежутки
возрастания и убывания функции: ![]()
4 Найти площадь фигуры ограниченной линиями у=3х , х=0, х=2.
5.Студенты одной группы должны сдать 4 экзамена в течение десяти дней. Сколькими способами можно составить расписание экзаменов, если в один день разрешается сдавать не более одного экзамена.
6. Программа экзамена содержит 30 вопросов. Студент знает 25 из них. Каждому студенту предлагают 2 вопроса, которые выбираются случайным образом. Положительная оценка ставится в том случае, если студент правильно ответил хотя бы на один вопрос. Какова вероятность успешной сдачи экзамена?
7. В двух ящиках находятся детали: в первом 12 (из них 4 стандартных), во втором 15 (из них 10 стандартных). Из каждого ящика вынимают на удачу по одной детали. Найти вероятность того, что обе детали окажутся стандартными.
8.Даны точки A(-4,-3,-5),B(1,-2,-8),C(3,2,-4),D(2,0,-1). Коллинеарны ли векторы АВ и СD, найти их длину и скалярное произведение.
