1.6. Графический способ вычисления интеграла Мора – способ Верещагина

Упрощение операции интегрирования основано на том, что эпюры от единичных усилий на прямолинейных участках оказываются линейными. Рассмотрим эту процедуру применительно к участку балки. На рис.1.16 сверху показан участок балки с эпюрой М_робщего вида, а внизу эпюра, представляющая линейную функцию. Преобразуем интеграл Мора

(а)

с учётом этой особенности. Как видно из верхнего чертежа, М_рdx = dω, а из нижнего чертежа имеем. Если кроме того считать, что жёсткостьEIна протяжении участка постоянна, вместо (а) будем иметь

. (б)

Интеграл представляет собой статический момент площади эпюрыМ_ротносительно осиу. Его можно записать иначе

S_y = ω ∙ x_c ,

где ω– площадь этой эпюрыМ_р;

х_с– координата центра тяжести эпюрыМ_р.

Рис.1.16

Отметив на нижней эпюре соответствующую ординату и обозначив её буквой m, будем иметь

x_ctg α = m.

В результате подстановки этих выражений в (б) получим

. (в)

Если балка имеет несколько участков по длине, формула Верещагина будет иметь вид

, (1.27)

где ∆ – обобщённое перемещение (либо прогиб υ, либо угол поворота θ);

ω_i– площадь эпюры моментов от внешней нагрузки (грузовой эпюры);

m_i– ордината единичной эпюры под центром тяжести грузовой эпюры;

n– число участков по длине балки.

При пользовании этой формулой надо уметь вычислять площади и координаты центров тяжести основных фигур: прямоугольника, прямолинейного треугольника и криволинейного треугольника. Минимально необходимые справочные данные приведены в табл.1.1. Процедуру графического вычисления называют «перемножением» эпюр.

В случае, если эпюра М_ртоже линейная, операция перемножения обладает свойством коммутативности: безразлично, умножается ли площадь грузовой эпюры на ординату единичной или площадь единичной на ординату грузовой.

Встречающиеся на практике эпюры могут быть, как правило, разбиты на простые фигуры, приведённые в табл.1.1.

Таблица 1.1

Эпюры Мри	Площадь грузовой опоры	Ордината единичной эпюры

Примечание: параболы – квадратные.

В качестве примера рассмотрим уже рассчитанную балку на рис.1.13. Чтобы построить эпюры М_р и , можно не определять опорные реакции: достаточно сосчитать момент на опореВ от нагрузки на консоли, построить эпюру на консоли, а затем соединить прямой линией значение М на опоре В с нулём на опоре А (рис.1.17).

В соответствии с формулой (1.27)

.

Конечно, результат получился такой же, что и при интегрировании по формуле Мора, но с меньшими затратами труда.

Рис.1.17

Глава 2. Статически неопределимые балки

2.1. Общие понятия

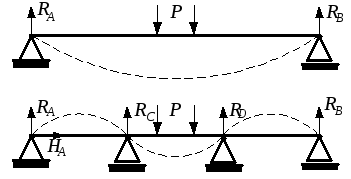
Изложенные в предыдущей главе методы определения перемещений широко применяются в расчётах статически неопределимых балок. Если при проектировании длинных балок (мостов, валов турбин) условия прочности и (или) жёсткости не выполняются, можно увеличить сечение балки, а можно поставить дополнительные опоры в пролёте (рис.2.1,б). Второй путь очень часто оказывается предпочтительным, так как позволяет, не увеличивая вес конструкции, сделать её более жёсткой.

а
б

Рис.2.1

Балка с промежуточными опорами становится статически неопределимой, так как трёх уравнений статики уже недостаточно для определения пяти неизвестных реакций.

Напомним, что простую статически неопределимую систему, образованную из стержней, работающих на растяжение-сжатие, мы рассматривали в разделе 2.5 первой части курса. Дополнительное уравнение для определения продольных сил в стержнях – уравнение совместности деформаций – было получено из рассмотрения схемы деформирования системы. Аналогичным по существу методом рассчитываются статически неопределимые балки.

Степень статической неопределимости определяется числом «лишних» связей. Балка на рис.2.1,б имеет две «лишних» промежуточных опоры – их можно удалить без ущерба для равновесия. Степень статической неопределимости этой балки равна двум.