1.4. Энергетические теоремы

В предыдущих параграфах настоящей главы определялись перемещения в балках с прямой осью. Ранее определялись перемещения прямого стержня при растяжении и кручении. Рассмотрим теперь универсальный метод, позволяющий определять перемещения в плоском или пространственном стержне, а также в кривом стержне. Этот метод – метод Мора – удобен также и для расчёта статически неопределимых балок, о чём будет сказано в главе 2. Метод Мора основан на энергетических теоремах, которые рассматриваются ниже.

1. Понятие о действительном и возможном перемещениях. Работа внешних сил

Условимся относительно обозначений. Перемещение какой-либо точки по определённому направлению от какой-либо силы или группы сил обозначается греческой буквой ∆, а перемещение от силы, равной единице, – буквойδ. Напоминаем, что перемещения определяются в линейно деформируемых системах (справедлив закон Гука), подчиняющихся принципу суперпозиции.

Различают действительное и возможное перемещения. К балке статически прикладываем силу Р(рис.1.9,а). Точка приложения этой силы перемещается на величину∆_рр. Первый индекс показывает точку и направление перемещения, второй – причину, вызвавшую данное перемещение. На рис.1.9,б показан график зависимости перемещений∆от изменяющейся во времени силыP_t. ∆_рр – действительное перемещение точки приложения силыР, вызванное её действием. Заштрихованная площадь треугольника определяет действительную работу, затраченную внешней силой на деформирование объекта

. (1.14)

Формула (1.14) представляет собой аналитическое выражение теоремы Клапейрона: действительная работа внешней силы равна половине произведения силы на перемещение точки её приложения по её направлению.

а б

Рис.1.9

Под возможным перемещением будем понимать бесконечно малое перемещение, допускаемое имеющимися связями и не зависящее от заданной системы сил. Рассмотрим балку, нагруженную силой Р(рис.1.10) и догрузим её силойК. Так как первоначальное перемещение∆_рр от действия силыРмалое, то добавочное перемещение∆_рк можно считать независимым от силыР, т.е.∆_рк – возможное перемещение (график на рис.1.10,б).

Возможной (виртуальной) работой силы Р называем работу этой силы на малом возможном перемещении. Виртуальная работа равна площади заштрихованного прямоугольника

. (1.15)

а б

Рис.1.10

Полная работа внешних сил для балки, показанной на рис.1.10,а, будет равна:

. (а)

Изменим порядок приложения сил (рис.1.11).

Рис.1.11

При таком варианте нагружения величина полной работы внешних сил будет равна:

. (б)

Ясно, что при любом порядке приложения сил величина полной работы одна и та же. Приравняв правые части формул (а) и (б), получим аналитическое выражение теоремы о взаимности возможных работ (теоремы Бетти):

Р∆_рк = К∆_кр. (1.16)

В случае равенства сил Р = Кполучим выражение теоремы о взаимности возможных перемещений (теоремы Максвелла):

∆_рк = ∆_кр . (1.17)

Если внешние силы не только равны друг другу, но каждая из них равна единице, формулу (1.17) можно переписать в виде

δ_ij = δ_ji , (1.18)

где iиj– номера единичных сил.

Формула (1.18) очень важна для расчёта статически неопределимых балок, о чём пойдёт речь в главе 2.

Можно заметить, что график на рис.1.9,б точно повторится и для других деформаций стержня: растяжение – P_t = Nи∆ = ∆ℓ; кручение –P_t = М_кри∆ = φ; изгиб при действии сосредоточенного момента –P_t = Ми∆ = θ. Поэтому во всех приведённых выше рассуждениях силуРможно трактовать как обобщённую силу, а перемещение∆– как обобщённое перемещение.

Под обобщённой силой подразумевают нагрузку в виде сосредоточенного усилия или момента, которые деформируют систему в условиях статического равновесия и совершают работу на соответствующих обобщённых перемещениях.

Под обобщённым перемещением понимают макродеформацию объекта в той точке, где приложена обобщённая сила.

2. Потенциальная энергия стержня. Теорема Кастильяно

График, приведённый на рис.1.9,б, представляет собой закон Гука для того или иного вида деформации стержня. Работа, затраченная на деформирование объекта, определяется формулой теоремы Клапейрона (1.14). При отсутствии энергетических потерь она равна потенциальной энергии деформации стержня U:

• для осевой деформации U = 0,5P∆ℓ; ;

• для кручения U = 0,5М_крφ;;

• для изгиба U = 0,5Мθ;.

Выполним операции дифференцирования:

• для осевой деформации ;

• для кручения ;

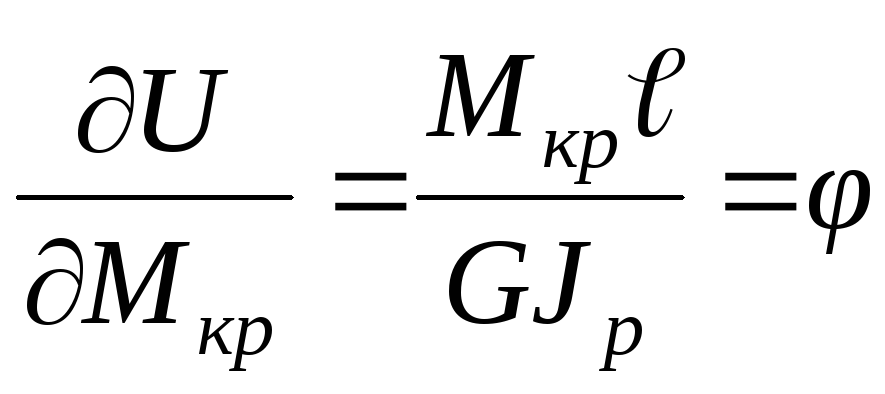• для изгиба .

Получены формулы, выражающие макродеформацию стержня через потенциальную энергию упругой деформации и совпадающие с точностью до обозначений. Их можно объединить одной записью:

. (1.19)

Формула (1.19) выражает теорему Кастильяно: частная производная от потенциальной энергии системы по силе равна перемещению точки приложения силы по её направлению. Теорема Кастильяно является главным звеном в системе энергетических методов расчёта.

Применим теорему Кастильяно к расчёту балок. Потенциальная энергия стержня при изгибе найдена ранее (см.п.5.10 первой части курса):

. (1.20)

Рассмотрим простой пример – защемлённую балку, нагруженную сосредоточенной силой (рис.1.12).

Рис.1.12

M = – P ∙ x; M² = P² ∙ x²; .

.

Получили известный результат – см.п.1.2.

В случае произвольного пространственного стержня, когда все шесть составляющих внутренних усилий ненулевые и меняются вдоль оси стержня, необходимо выделить в стержне элемент бесконечно малой длины и последовательно подсчитать энергию, накапливаемую в результате осевых, крутильных, изгибных и сдвиговых деформаций:

• для осевой деформации ;

• для кручения ;

• для изгиба и;

• для сдвига и(коэффициентыk_yиk_zзависят от формы поперечного сечения и составляют величину порядка 1, 2).

Для подсчёта потенциальной энергии стержня необходимо просуммировать элементарные значения dUпо всей длине стержня:

. (1.21)

Последними двумя слагаемыми, как правило, пренебрегают ввиду их малости по сравнению с предыдущими. Подставив (1.21) в (1.19), получим:

. (1.22)

где ∆- обобщённое перемещение (линейное или угловое);

Р– обобщённая сила, приложенная в той точке, в которой определяется перемещение (сосредоточенная сила или сосредоточенный момент).

Формулу (1.22) можно распространить на случай стержневых систем, состоящих из многих стержней (рам или ферм). Для этого надо в (1.22) перед каждым интегралом ставить знак суммирования.