Круговая интерполяция с использованием

оценочной функции.

I квадрант.

F(,)>0

R F(,)=0 решение траектории

движения изображающей

F(,)<0 точки



Если дуга окружности в других квадрантах, то

№ квадранта	Направление
			
	х	у	Х	у
1 2 3 4	 - - 	  - -	 - - 	  - -

F(,)=²+²-R²

Пересчёт значений F(,) для движения по часовой стрелке ().

а) При шаге по  (если (F(i,i)0))

F (i+1, i) = (i+1)²+i²-R²=F(i,i)+2i+1

F

б) При шаге по  (если F(i,i)>0)

F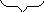(i, i+1)=i²+(i-1)²-R²=F(i,i) - 2i + 1

F

Для повышения скорости движения алгоритм пересчёта F(,) можно усовершенствовать с учётом того, что:

а) При 0<<45 (1 участок) – ведущая координата.

б) При 4590 (2 участок)  - ведущая координата.

Тогда: F(i+1, i+1) = F(i+1,_i-1) = F(i,i) + 2(i - i) + 2

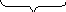
F

Приращением 1 соответствует элемент движения F по  и  на dz.

Fi – частота шагов (определяет контурную скорость).

Если fi=const, то движение по окружности будет с Vk=var (переменным), что нежелательно с технологической точки зрения.

Поэтому: fi+1=fiVk/R

Где «+» – для первого полуквадранта,

«-»  для второго полуквадранта.

 Тогда Vk – const.

Алгоритм круговой интерполяции.

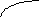
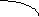
Начало

(2 участок) Нет Да (1 участок)

i-i

Нет Да Нет Да

Fi0 Fi0

Fi+1=Fi+2 Fi+1=Fi+ Fi+1=Fi+ Fi+1=Fi-

2(i+i)+2 +2(i-i)+2 -2i+1

Шаг по  i+1=i-1 i+1=i+1 Шаг по 

fi+1=fi-Vk/R fi+1=fi+Vk/R

i+1=i+1 Шаг по  i+1=i-1 Шаг по 

Обработка по идля

окончательного раннего кадра

движения УП

Конец

Если заданная дуга окружности расположена в нескольких квадрантах, то её разбивают на соответствующее число устройств, и каждый из них записывается в данный кадр.

Достоинства: Простота реализации.

Недостаток: Vk (скорость) мала. Контурная скорость ограничена из-за необходимости отработки приводами элементарных приращений с частотойfi.

В современных ЧПУ – такие алгоритмы применяются редко (NC типа) – с жёсткой реализацией алгоритма и дискретными приводами с шаговыми двигателями.

Более широкое применение в СNC – типах систем находят методы интерполяции в кодовых приращениях (определяютсяхтиут, а в абстрактныхтит) за времяTk – период квантования управляющих воздействий. Процедура их расчёта базируется на моделировании движений изображающей точки с оценочной функцией в ускоренном масштабе времени начиная с большего шага:

H0>>dz (пои) и заканчивается шагом.

Hm = dz, где k=0,1,2,...,m– номер шага.

1 этап: вычисление т, т

2 этап: их выдача i=i+т

i=i+т

Методы интерполяции «цифра за цифрой».

Здесь числа рассматриваются как композиции цифр с основанием q, зависящим от использования системы счисления. Для двоичных системq=2.

n

В общем, виде x = (iq^-i)

i=1

число

где Ai{0,1,2,...,q^-1}

Алгоритмы этих методов мы используют итерационную процедуру: U[k+1] = f{u[k]}, однократное применение которой даёт одну достоверную цифру результата, аn – кратное –n – верных результатов (цифр).

Такие методы появились в начале ХVIIвека.

а) Работы 2-х авторов Вагдер и Меджер.

Ими были разработаны алгоритмы для вычисления:

• элементов f(x) (показательных, прямых и обратных тригонометрических, логарифмических, гиперболических).

• множительно – делительные (х/yz).

• корневые хi у , ³х/у...

• векторных преобразований.

Основные положения метода.

Если U(x) – заданная функция,X – аргумент.

U0(x) – известные начальные значения.

Иерархическая формула:

U[k+1] = U[k] + i[k]

i –скаляр (величина шага итерации).

+1

[k] = -1 направления движения

i[k]=U[k] –приращение.

При этом i изменится вq – раз (напримерq=2) при получении очередной верной функции искомой функции.

Алгоритмы этих методов 2-х этапные.

а) На первом этапе формируются последовательные значения [к]

[1][2]...[kmax]

Kmax зависит от разрядности представленных используемых чисел (x, u(x))

б) Строится итерационный процесс и определяется последовательность

[1] [1] n

U[0]=  U[1]=   u[kmax]

[1] [2] n

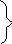0 для разных

u0(x) = 1 U(x) свои случаи

C0 – некоторая константа

Отличительной особенностью алгоритмов этих методов является наличие в них только коротких операций (сложение, вычитание сдвигов влево, вправо).

Примеры рекуррентных выражений для вычисленных функций sin  иcos .

1 этап:

Qk+1=Qk - karctg (q ^-i)

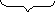
табличное значение

k = sign (Qk)

k=0,1,...kmax

Начальное условие: Q0=0

Определяем знаки К-ые, Кmax – зависит от требуемой точности вычислений.

2 этап: yk+1=yk-kxkq^-i - дляsin 

xk+1=xk+kykq^-i - дляcos 

Начальное условие у0=0, х0=1/

где =1,646 – масштабный коэффициент.

При к=m ym = -sin 

Хm = cos 

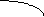
Алгоритм круговой интерполяции по методу «цифра за цифрой» Меджита.

(q=2, замена переменнойqⁱ yi=zi)

x = R cos ; y = R sin 

Для 1 – го этапа:

Qi+1 = 2  ( Qi - i  2^-i  arctg 2^-i )

i = sign Qi

1. *.

2. вычисление тригонометрических функций cos , sin .

___

где Q0=; i=0,n – гдеn – число достоверных разрядов.

Для 2-го этапа

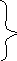
Zi-1=2^-1(Zi+Xi)

Xi-1=Xi - i-12^-2(i-1)Zi

где i=n, n-1, ... 0

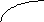
Начало

1

Хn=R/M; 0,  0=arctg(Iнач/Xнач)

i=0; Q0 =VkTk/R

приращение угла

2

i = sign Qi

3

И запоми - Да Нет

наемi 4 i<0 5

Qi+1=Qi+ Qi+1=Qi-

+2ⁱarctg2^-i -2ⁱarctg2^-i

6

Qi+1=Qi+1/2

. . . . Блок 1-7 результирует

i=i+1 1 этап алгоритма

Нет 7

i=n

Да

Да 8 Нет

i<0

9 10

Zi-1=(Zi-Xi)/2 Zi-1=(Zi+Xi)/2

Да 11

I<n/2

12

Zc=Zi2^-2(i-1)

Да 13 Нет

14 i<0 15

Xi-1=Xi+Zc Xi-1=Xi-Zc

16

i = i-1 Блоки 8-17

реализуют

2 этап

17 алгоритма.

Нет

i = 0

Да

Конец

Назначение блока № 11: при i>n/2 Zcвыходит за разрядную сетку, что позволяет сократить время счёта.

Межтактовые приращения вычисляются по значениям х0и у0для соответствующих шагов интерполяции.

хт[к]=х0[k-1]x0[k]

yт[k]=y0[k-1]y0[k]

где х0[k], x0[k-1], y0[k], y0[k-1] – вычисленные по приведённому выше алгоритму (на соседних шагах) верхние знаки («-» и «+») соответствуют движениям против часовой стрелки, нижним – по часовой.

Алгоритм линейной интерполяции по методу «цифра за цифрой» Меджита – аналогичен предыдущему, но:

а) в блоке № 1 хn = L/M гдеL=VkTk – приращение пути заTk.

б) в блоках 4 и 5 таблицы констант заменяются на единичное значение arctg (yкон/xкон)

в) Вычисляем значения x0 и у0являются приращениями констант заTk.

x[k]=x0[k]; y[k]=y0[k]

Оценка требуемой разрядности n.

1. При линейной интерполяции.

а) Lmax=Vk max, max[inf Tk] = 10 м/c*0,01 c =0,1 м

inf – максимальное значение из минимального, т. е.inf Tk –нижняя граница Тk.

Lmax 0,1

Следовательно:  =  = 10⁵, то есть 1666 бит< 2¹¹-1

min dz 10^-6

или n=11.

2) При круговой интерполяции.

а) Rmax = 10 m

б) min dz = 10^-6 m   min = (min dz)/(Rмах)=10^-6/10=10^-72^-24 илиn=24

т. о. Rmax=2²⁴dz

Вывод: методы «цифра за цифрой» позволяют минимизировать временные затраты на реализацию алгоритмов с учётом типа интерполяции.

Время вычисления sin  (илиcos ).

а) на К580 6 мс

К1810  1,5 мс.

Таблично – аналитические методы интерполяции (4-я группа).

Чисто табличные методы не применяются.

f(x)

2ⁿ – для указанных операций,n – разрядных операндов.

2²ⁿ – для бинарных операций.

Объём ПЗУ в словах.

XПЗУ f(x) – значение(двоичный код)

f(x)

адрес

(двоичный код)

Пример: R=10 м, dz=1 мкм

2²ⁿ 1,7*10⁶ – 24 разрядных слов

требуется ПЗУ объёмом 5,1*10⁴ Кбайт = 51 МБ для хранения значенийsin  c точностьюdz.

Достоинства: Отсутствует накапливающееся погрешность. Упрощаются итерационные процедуры.

В качестве аппроксимирующей функции используют итерационные полиномы Лагранжа, Ньютона, а в зависимости от числа учитывающего табличные значения применяют линейную, параболическую, кубическую аппроксимацию.

Кусочно-линейная аппроксимация (интерполяция) по формуле Ньютона:

f(x) = f(xi)+(f(xi+1) - f(xi))/(xi+1-xi)(x-xi) = f(xi+kix)

где f(xi); f(xi+1) – табличные значения.

xi+1-xi=xi – итог таблицы.

Шаг таблицы, конечно, оценивается требуемой погрешностью аппроксимации:

хi  [d²f(x)/dx²при х=хi ^-1а]^1/2

где d²f(x)/dx²^-1- обратная величина модуля второй производной.

а– максимальное значение ошибки аппроксимации х[хi, xi+1]

Для ф-й sin  иcos  приsin =cos =1

___

= - постоянный шаг в таблице (на апроксимации для табличных значенийsin  иcos ).

. . . . .

Так какsin  = sin  sin max = 1

. . .  . .

 cos  = cos  cos max = 1

Чтобы избежать в последующих (операциях) вычислениях операций умножения и деления, заменив их на операции сдвига кодов, а также чтобы использовать коды значений аргумента в количестве адресов, по которым хранятся коды значений аргумента в количестве адресов, по которым хранятся коды значений функции необходимо шаг по аргументу выбрать равным целой степени основания систем счислений.

 хi+1 = xi+1 – хi = q^-(n-r) =2^-(n-r)

шаг по аргументу

где (n-r) – разрядность, кода старшей части аргумента xi(являющейся адресом, «грубые» значения функций в таблице ПЗУ).

Для таблицы sin  и cos  шаг:

  2^–(n-r)

Оценка объёма ПЗУ (пример). Если таблица содержит 25 – разрядные значения функции, то есть n = 25, a(n-r) = 12 разрядов адреса, тогда при R = 10 м и dz = 1 мкм для хранения опорных точек на дуге окружности первого квадранта требуется N = 3835 опорных точек, так как N = R/4Rarcsin(2²dz/2/R) = R/(2^N+1dz⁾ – это отношение длины дуги (R/2) к длине дуги, стягиваемой аппроксимированной хордой  объём ПЗУ Q = 2(N-1)*2²⁵ бит =

= 23963 байт = 24 кБ

Другой способ представления таблиц:

• не в абсолютных значениях sin  и cos , а в приращениях их смежных значений:

хi = xi – xi-1= R(cos i – cos i-1) = R  cos  i

yi = yi – yi-1= R(sin i – sin i-1) = R  sin i

Это позволяет вдвое уменьшить объём таблиц.

Вычисление поправок (к табличным значениям функции) – это типичная интерполяционная задача, которая может решаться любым

рассматриваемым ранее методом.

Учитывая разнообразие форм представления таблиц и разнообразие алгоритмов вычисления поправок, становится понятным, что группа табличных алгоритмов является наиболее многочисленной.

Обобщённая схема алгоритма линейно – круговой интерполяции таблица алгоритмического типа.

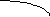
Начало

вычисление

sin , cos  1 этап

xi = Rcos

yi = Rsin

xт = xi-1 – xi 2 этап

Только yт = yi-1 – yi

при

круговой  =  +

интерпо-

ляции

Конец

Здесь R = - радиус при круговой интерполяции.

- угол наклона прямой

 =

- центробежный угол окружности