
- •Кдос. П.
- •1 Работа.
- •Цифровое Обработка Связь с Диагностика
- •Показатели качества, основные характеристики
- •Организация в однопроцессорном учпу.
- •Методы и средства программного
- •Классификация методов интерполяции
- •Обобщённая схема алгоритма интерполяции
- •Запрос на прерывание о
- •Метод двойной рекурсии
- •Методы и алгоритмы интерполяции
- •Алгоритм линейной интерполяции с оценочной
- •Круговая интерполяция с использованием
- •Обработка по идля
- •Расчёт эквидистантного
- •Ошибки воспроизведения типовых участков
- •При воспроизведении прямой под углом
- •Искажение геометрических форм
- •Влияние «неидеальностей» кинематических цепей
- •Символы с необязательным семантическим
- •Структурное программирование
- •Автоматизация программирования процессов
- •Обобщённая структура арт – образных
ПУС.
Типовая схема контурного фрезерования.



Кдос. П.

_












 X
X
X
X








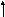
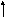
 Wx
Wx









 fx
fx
Wxx Wyx Wzx



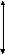
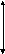
 _
_
_
_
 Р
fp
Р
fp











 Wp
WСПИД
Wp
WСПИД











 Wxy
Wyy
Wzy
Wxy
Wyy
Wzy



 _ _
_
_
_ _
_
_


 yвх fy
Y P
Y
yвх fy
Y P
Y


















Wy





 Kдос.
п.
Kдос.
п.

Блок – схема систем ЧПУ станком.















 1 2
3 4 деталь
1 2
3 4 деталь


































 1 2
3 4 5 6 7 8
1 2
3 4 5 6 7 8









 fx
fx








 _
Wx
_
Wx

 ЧПУ
ЧПУ

 fy
fy








Wy

 _
_

Повышения живучести производства потребовало создания ГПС, в основе которой лежат станки с ЧПУ.
1 – Чертёж
2 – Таблица исходных данных.
3 – Программоноситель.
4 – Станок.
Целью ЧПУ является чертёж превратить в готовую деталь.
1 – Составление и запись программ в текстовой форме (инженер – технолог).
2 – Ввод информации на носитель, контроль правильности.
3 – Ввод информации в станок.
4 – Блок управления.
5, 6 – Привод исполнительного узла.
7 – Ходовой винт.
8 – Датчик информации.
(Михеев, Сосонкин. Программное управление станками.)
WСПИД – ПФ станок – приспособление – изготовление – деталь.
ПФ технологические системы.
Формируется сила резания, которая носит пространственный характер и распределяется по составлению и воздействию в качестве возмущения на силовые элементы.
fx , fy – случайные помехи.
Wx, Wy – ПФ координация привода.
Таким образом, мы видим, что система управления в процессах контурного фрезерования представляет собой сложную, взаимосвязанную, иерархическую систему управления.
Сделаем разумное допущение:
Будем отдельно рассматривать следующие привода координационных систем от процессов резания, а силу резания будем рассматривать в качестве возмущения на следящие привода.
(мелкий рисунок).
Данная система контурного управления конической.
Вообще – то проблема повышения точности обработки весьма многогранна.
В общем, балансе погрешности детали, погрешность от следящих приводов может составлять до 60 % .
В практических случаях любая траектория апроксимируется отрезками прямых линий и дугами окружностей.


c
R
b
a
Здесь мы можем выделить 3 основных режима резания:
1 – Режим позиционирования. Необходимо перемещать точку в конечное положение за минимальное время. (Зависит от производительности станка).
Типовой станок – ступенчатое воздействие.
2 – Обработка линейного задающего воздействия.
3 – Обработка задающего гармонического воздействия.
Точностные показатели.
Мы будем различать контурную погрешность (нормальный привод от реального контура к желаемому).
 формообразование
формообразование



 волнистость
1
волнистость
1








 шероховатость
2
шероховатость
2













Контурная погрешность.
1 1
= K [ – ]

 Kx
Ky
Kx
Ky



 V
V
= [ 1 - Ф (j)]
R
(Лебедев, Орлова, Пальцев. Следящий ЭП станков с ЧПУ.)
Кх, Ky – добротность следящих приводов.
Ф(jw) - модуль частотной характеристики.
V – контурная скорость.
R – радиус закругления.
(Андрейчиков. О повышении динамической точности станков с ЧПУ.)
Так как идентичности следящих приводов добиться очень сложно, то основным способом повышения точностных характеристик является повышение качественных характеристик координации следящих приводов.
Мы знаем:
моментная погрешность
скоростная погрешность
динамическая погрешность
 х
х
х
х

 tв
tв






 хстат
хстат
n


 дин
t
t
дин
t
t

 0
0
0
0
n – динамическая проверка скорости.
В настоящее время проблем со статическими и моментальными погрешностями практически нет, из – за получения высокого коэффициента усиления, а также введения интегрирующих составляющих в закон управления.
(В станках с ЧПУ используется, как правило, П – регулятор положения)
Проблема динамической точности существует.
Основным путём повышения динамической точности является путь повышения быстродействия системы. Однако, он ограничен ростом в переход, режимах работы динамических перегрузок, поэтому наиболее перспективными методами являются программные методы коррекции.
Постановка задачи синтеза программного управления.
А (р) J(t) = B(p)(t)


 (t)
Y(t)
(t)
Y(t)

 W(s)
W(s)

T1
[ Y*(t) – Y(t) ]2 dt (*)
0
Необходимый синтез закона управления (t) из условия (*), где
Y*(t) – желаемая траектория
Y(t) – реальная траектория
Формально задача решается путём использования операций обращения:
(t) = B(p)-1A(p)Y*(t)
B(p) = bm
Однако данный имеет существенный недостаток – высокий рост шумов, связанный с использованием операций дифференцирования.
(Башарин, Постников. Примеры расчёта систем электропривода на ЭВМ.)
Что в конечном итоге вызывает необходимость использования специальных процедур сглаживания и регулирующих.
B(p) = b0p + b1
В данном случае задача решается в 2 этапа.
1 – вычисляют функцию y(t) = A(p)Y*(t)
2 – численно решают ДУ x(t) = (b0p+b1)(t)
Однако использование численных методов ставит под сомнение возможности синтеза программного управления в реальном масштабе времени.
Синтез программного управления для управления скоростью ДПТ (Л. р. № 1).
Управление угловой скоростью исполнительного элемента.
В качестве исполнительного элемента рассматривается двигатель постоянного тока с независимым возбуждением, ПФ которого:
1
W(s) = ; C2 = 0,4377 Bc/рад
C2(T1T2s2+T1s+1)
T1 = 0,0289 c , T2 = 0,013 c
Задача решается при нулевых начальных условиях. В качестве желаемой траектории выбираем траекторию с ограничением ускорения и скорости нарастания ускорения выходной координаты (рис.1, кривые 1, 2).
 V(t);
A(t)
V(t);
A(t)

 2
1
2
1






am S



Lty Lty
ty

В соответствии с формулами Эйлера гармоники тригонометрического ряда (5):

Ak = E(-sin (R) – sin (RL/(1-L)) + sin (R/(1 – L)))
Vmm2(1-L)
E =
2L()3
Bk = E(-1 + cos (RL/(1-L)) + cos (R) – cos (R/(1-L))) (7)
R = 2/m A0= Vm/2 am = Vm/ty/(1-L)
T TL T 2
tx = ; t1 = ; t2 = ; m
m(1-L) m(1-L) m 1-L
где ty – время управления
Vm, am – максимальные значения скорости и ускорения выходной координаты.
Пусть Vm = 1 рад/c; L = 0,25; m = 3; T = 0,314 c,
что соответствует am = 9,55 рад/c2; tу = 0,14 c; t1 = 0,035 c;
t2 =0,104 c гармоники управляющего воздействия.
V(t) = P0 + Pкcos(kt) + Tksin(kt) (6)
k=1 k=1
находим по частотным характеристикам (s) или по формулам
Pк = - C2T1T2k22Ak + C2T1kBk +C2Ak; P0=C2A0
Tk = - C2T1T2Bkk22 – C2T1kAk + C2Bk
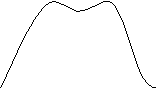
На рис. 3 представлены:
Графики скорости и ускорения (1, 2) рассчитанные в соответствии с (7) с точностью до 50 – й гармоники.
Графики скорости и ускорения (3, 4) выходной координаты при подаче управляющего воздействия (6) с точностью до 5 – й гармоники.
График управляющего воздействия (кривая 5) рассчитывается в соответствии с (6) с точностью до 5 гармоники.
V(t) a(t) x(t)
 2
4 1
2
4 1







 0,5
10 1,0
0,5
10 1,0
 0,4 8 0,8
0,4 8 0,8



 5
рис. 3.
5
рис. 3.


 0,3 6 0,6
0,3 6 0,6



 0,2 4 0,4
0,2 4 0,4
3


 0,1 2 0,2
0,1 2 0,2



 0
0
0,04 0,08 0,12 t, с
Управление угловым перемещением.


 y*(t)
y*(t)

 W(s)
W(s)
 (t)
=?
(t)
=?
T1
J = [Y*(t) – Y(t)]2 dt
0
W1(s) = 1/Kе/(T1T2s2 + T1s +1) двигатель по скорости
W2(s) = 1/Kер/(T1T2s2 + T2s +1) двигатель по углу
W3(s) = (а3s + a4)/(s4 + a1s3 + а2s2 + а3s + a4)
W4(s) =W3(s) система позиционирования















 a3
s3
+ a4
s2
1
1
a3
s3
+ a4
s2
1
1









 s4+a1
s3+a2
s2+a3
s+a4
s s
s4+a1
s3+a2
s2+a3
s+a4
s s
.. .
(t) Y(t) Y(t) Y(t)

















 P0
P0















 t
=1
Asint
t
=1
Asint











 t
=1
Pcost
t
=1
Pcost














 t
3
T3sint
t
3
T3sint



К это !
