Пример расчета Подбор сечения стержня при заданной нагрузке
З а д а н и е и и с х о д н ы е д а н н ы е
Для стержня, показанного на рис. 3.8,
подобрать поперечное сечение. Форма
поперечного сечения дана на рис. 3.9.
Исходные данные приведены в табл. 3.2.
Модуль нормальной упругости
и допускаемое напряжение принять
равными:
для дерева
МПа
кН/см2и
МПа
кН/см2;
для чугуна
МПа
кН/см2и
МПа
кН/см2.
Таблица 3.2
|
Устойчивость |
Поперечный удар | ||||||||||||||
|
Подбор сечения |
Определение грузоподъемности | ||||||||||||||
|
Номер строки |
Рис. 3.8. |
Рис. 3.9. |
кН |
м |
МПа |
|
Рис. 3.8. |
Рис. 3.11. |
Номер строки |
м |
Рис. 3.14. |
Номер профиля |
кН |
м |
см |
|
1 |
1 |
1 |
35 |
0,5 |
10 |
0,2 |
3 |
1 |
10 |
1,5 |
1 |
24 |
10 |
1,2 |
3,5 |
|
2 |
2 |
2 |
36 |
0,6 |
10 |
0,2 |
4 |
2 |
10 |
1,6 |
2 |
24а |
14 |
1,4 |
3,0 |
|
3 |
3 |
3 |
37 |
0,7 |
10 |
0,2 |
2 |
3 |
14 |
1,7 |
3 |
27 |
15 |
1,6 |
2,5 |
|
4 |
4 |
4 |
38 |
0,8 |
10 |
0,3 |
1 |
4 |
16 |
1,8 |
4 |
27а |
20 |
1,8 |
2,0 |
|
5 |
4 |
5 |
39 |
0,9 |
10 |
0,3 |
2 |
5 |
18 |
1,9 |
5 |
30 |
22 |
1,9 |
2,0 |
|
6 |
3 |
1 |
40 |
1,0 |
100 |
0,3 |
3 |
6 |
18 |
2,0 |
6 |
30а |
25 |
2,0 |
1,5 |
|
7 |
3 |
2 |
41 |
1,1 |
100 |
0,4 |
4 |
7 |
20 |
2,1 |
7 |
33 |
28 |
2,2 |
1,2 |
|
8 |
4 |
3 |
42 |
1,2 |
100 |
0,4 |
3 |
8 |
20 |
2,2 |
8 |
36 |
30 |
2,4 |
1,2 |
|
9 |
3 |
4 |
43 |
1,3 |
100 |
0,4 |
1 |
9 |
22 |
2,3 |
9 |
40 |
32 |
2,6 |
1,0 |
|
0 |
4 |
5 |
44 |
1,4 |
100 |
0,4 |
2 |
10 |
22 |
2,4 |
0 |
45 |
35 |
2,8 |
1,0 |
|
|
е |
е |
д |
е |
е |
а |
е |
е |
д |
д |
е |
а |
д |
д |
б |
,
,
,
,
,
,
Р е ш е н и е
Вычертим схему стержня и поперечное сечение (рис. 3.10). Проставим на схеме размеры и нагрузку, материал – чугун, коэффициент условия закрепления концов стержня принимаем по рис. 3.2.
Расчет необходимо начать с определения геометрических характеристик:
наружный
диаметр
;
внутренний
диаметр
;
площадь
поперечного сечения
;
момент
инерции 
;
радиус
инерции 
.
Подбор сечения произведем из условия устойчивости (3.11).
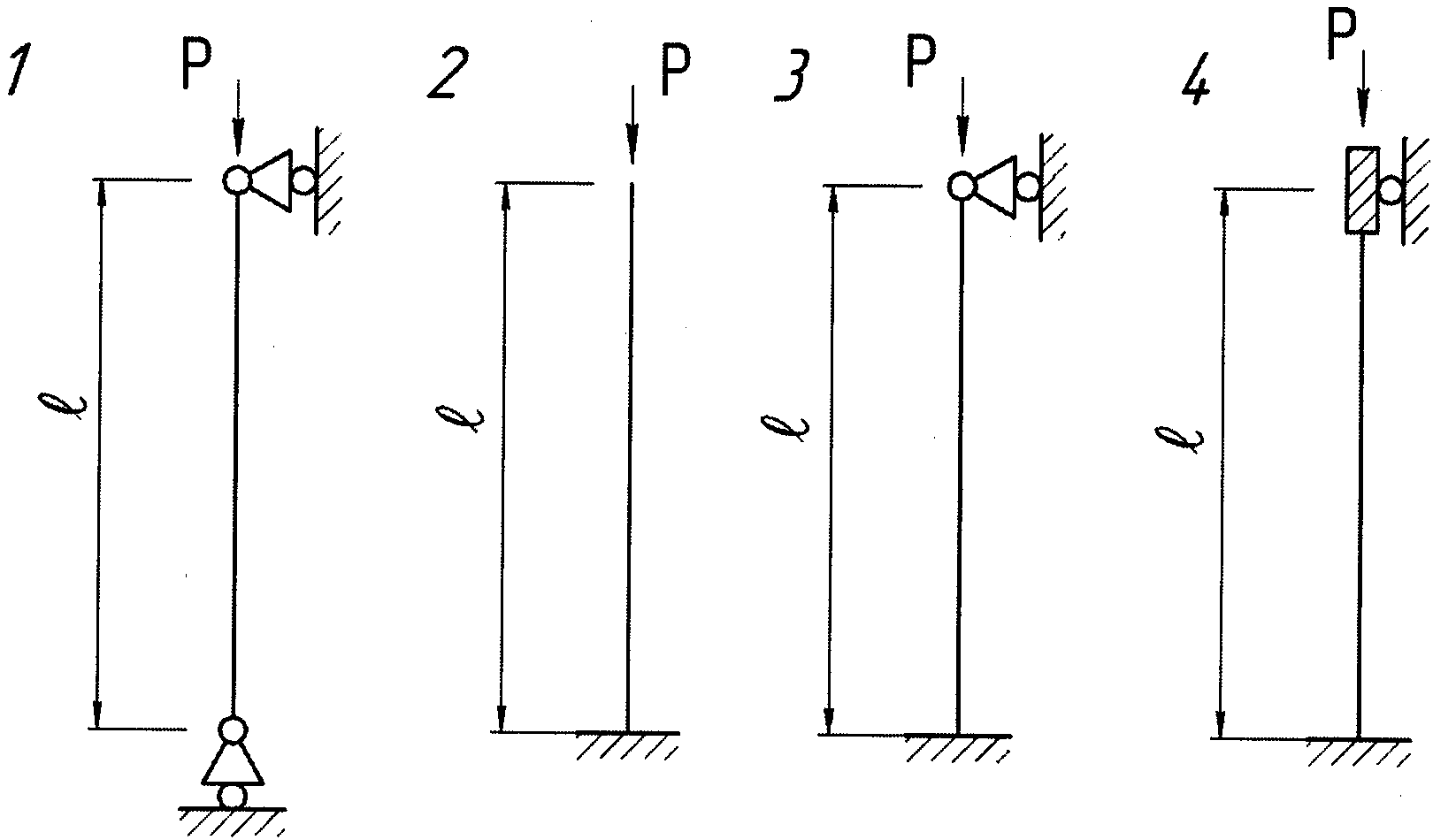
Рис. 3.8. Схема сжимаемого стержня
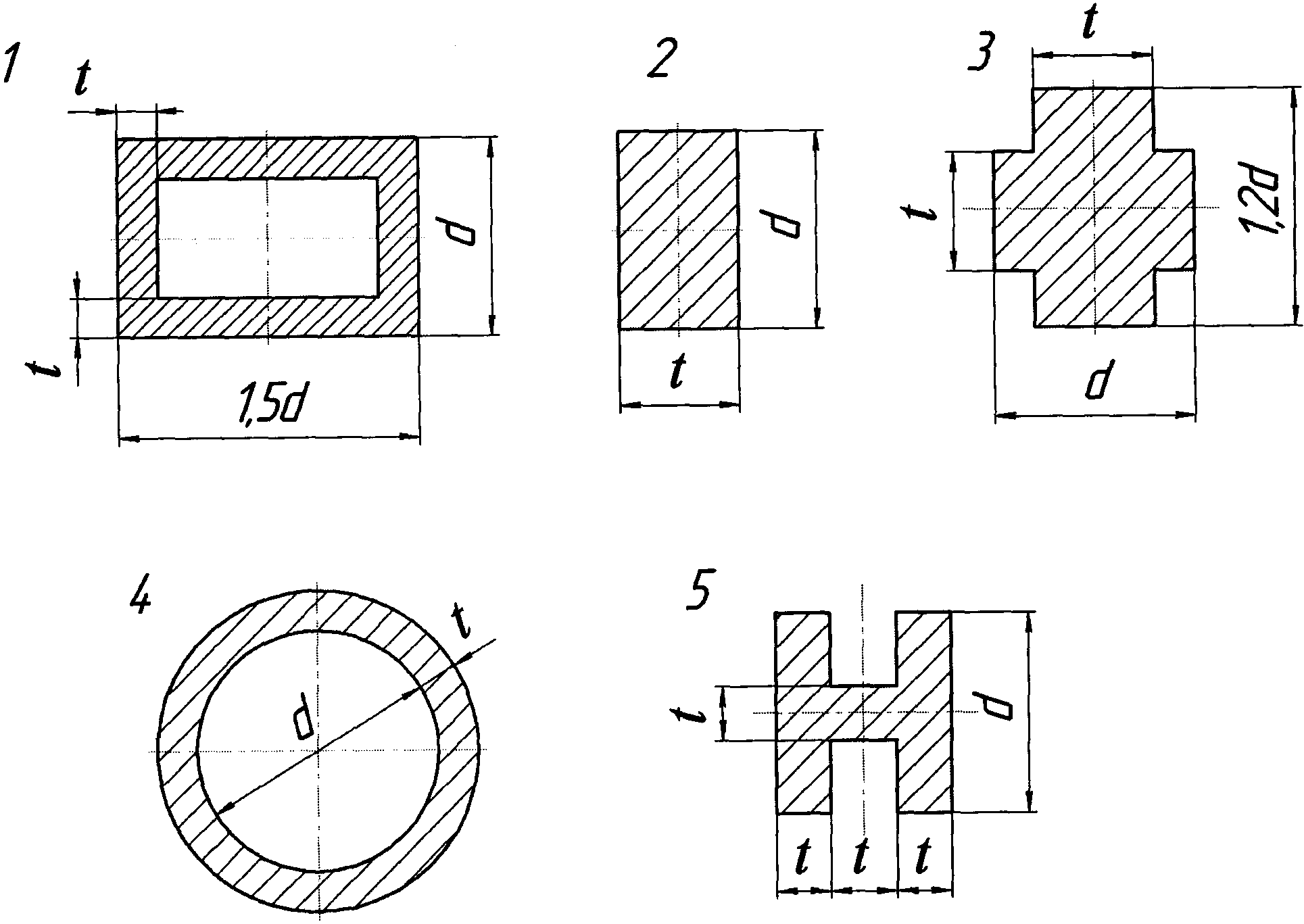
Рис. 3.9. Поперечные сечения стержня (к задаче №1)
Рис. 3.10. Схема к определению размеров поперечного стержня
Рис. 3.11. Поперечные сечения стержня (к задаче №2)
Ввиду того, что коэффициент
неизвестен и зависит от размеров
поперечного сечения, которые надо
определить, задача решается методом
последовательных приближений. Зададим
коэффициенту,
изменяющемуся в пределах
,
произвольное значение.
1. Принимаем
см2;
см;
см.
Гибкость
.
Из
табл. 3.3 находим
.
Найденное значение отличается от
первоначально принятого
.
Поэтому переходим ко второму приближению.
2. Принимаем
.
см2;
см;
см.
Гибкость
.
В табл. 3.3 гибкость
изменяется с шагом 10, поэтому для
определения
,
соответствующего
,
произведем линейную интерполяцию
|
|
|
|
40 |
0,69 |
|
50 |
0,57 |
.
Полученное значение
совпало с исходным
,
поэтому вычисления можно закончить.
Сделаем проверку устойчивости.
Действующее в стержне напряжение
кН/см2.
Допускаемое напряжение
кН/см2.
Условие устойчивости обеспечено. Таким обратом, чугунная труба имеет размеры:
внутренний
диаметр
см;
наружный
диаметр
см.
Таблица 3.3
Коэффициент
|
|
Ст.3 |
Алюминий |
Чугун |
Дерево |
|
0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 |
1,00 0,99 0,96 0,94 0,92 0,89 0,86 0,81 0,79 0,69 0,60 0,52 0,45 0,40 0,38 0,32 0,29 0,26 0,23 0,21 0,21 |
1,00 1,00 0,92 0,85 0,78 0,72 0,64 0,56 0,49 0,39 0,32 0,96 0,22 0,19 0,16 0,14 - - - - - |
1,00 0,97 0,91 0,81 0,69 0,57 0,44 0,34 0,26 0,20 0,16 - - - - - - - - - - |
1,00 0,99 0,97 0,93 0,87 0,80 0,71 0,60 0,48 0,38 0,31 0,25 0,22 0,18 0,16 0,14 0,12 0,11 0,10 0,09 0,08 |
