2.5.2. Температурные напряжения

В элементах статически неопределимых конструкций при изменении температуры возникают усилия (напряжения). Статически определимые конструкции при изменении температуры деформируются свободно: если нагреть стержень на ∆Т градусов, то он удлинится (рис.2.12) на величину ∆ℓ_Т.

Рис.2.12

∆ℓ_Т = α ∙ ∆Т ∙ ℓ, (2.19)

где α – коэффициент линейного расширения, размерность – 1/ град.

Превратим стержень, показанный на рис.2.12, в статический неопределимый. Для этого справа установим жёсткую опору (рис.2.13).

Рис.2.13

Теперь при нагревании жёсткие опоры препятствуют удлинению стержня, в результате чего возникают реакции, направленные вдоль оси. Уравнение статики:

∑ х = 0: R_B – R_A = 0  R_B = R_A = R.

Уравнение совместности деформаций:

∆ℓ = ∆ℓ_Т + ∆ℓ_N = 0 .

Записываем физическое уравнение, помня о том, что обе составляющие имеют знак “ + “, т.к. продольная сила N = R – растягивающая и от нагревания стержень должен удлиняться:

.

Получаем формулу для напряжения в стержне при равномерном по длине нагреве

. (2.20)

Теперь вернёмся к ферме, показанной на рис.2.11, и определим напряжения, возникающие в её стержнях, при равномерном нагреве одного из них. Внешняя сила Р при этом отсутствует. Исходные данные – в табл.2.2. Узел А – на рис.2.11,б, Р = 0.

Таблица 2.2.

Стержень		Площадь поперечного сечения F, см2	Коэффициент линейного расширения α, 1/град	Изменение температуры ∆Т0, С
1		10,6	225·10-7	+40
2		21,2
1.	∑ х = 0: N3sin 300 – N2sin 300 = 0  N3 = N2, ∑ у = 0: N1 – 2N2cos 300 = 0.					(а)

2. Схема деформации – на рис.2.11,в, уравнение совместности деформации остается то же самое

∆ℓ₂ = ∆ℓ₁ ∙ cos 30⁰. (б)

3. Физическая сторона задачи:

,

.

В первом уравнении поставим знаки “–“, т.к. на схеме деформации системы первый стержень укорачивается. Теперь выражения для ∆ℓ подставляем в уравнение совместности деформаций (б):

.

Получили 8,16N₂ + 24,5N₁ = – 2338,2. (в)

4. Синтез. Решаем систему уравнений (а) и (в):

Получаем N₁ = – 80 кН, N₂ = – 46,26 кН.

5. Расчёт на прочность:

, .

Напряжения меньше допускаемых (см. табл.2.1), прочность обеспечена.

2.5.3. Монтажные напряжения

Свободная сборка статически неопределимых конструкций возможна при точном изготовлении их элементов. При отклонении размеров элементов от номинальных сборку можно осуществить с приложением усилий, вызывающих деформации элементов, поэтому в них после монтажа системы будут напряжения, называемые начальными или монтажными. В статически определимых конструкциях неточность размеров элементов не требует применения усилий при монтаже, и в элементах не возникают начальные напряжения.

Снова рассмотрим трёхстержневую статически неопределимую ферму и определим монтажные напряжения при условии, что длина первого стержня оказалась короче номинальной на величину δ (рис.2.14 и табл.2.3).

а б

Рис.2.14

Таблица 2.3

Стержень	Площадь поперечного сечения F, см2	Модуль Юнга E, кН/см2	Неточность изготовления δ, см
1	10,6	104	-0,3
2	21,2	2·104

Если величина δ незначительна по сравнению с длинами стержней, то приложив определенные усилия, можно все три стержня соединить в узле, который займёт положение А′ ( рис.2.14,б). Очевидно, при этом все стержни будут растянуты, поэтому схема сил на рис. 2.11, б (Р = 0).

1. Статическая сторона этой задачи совпадает со статической стороной задачи о температурных напряжениях. Уравнения статики те же самые:

   ∑х = 0: N3sin 30 – N2sin30 = 0, N3= N2, ∑y = 0: N1 – 2N2cos30 = 0.

   (а)

2. Геометрическая сторона задачи. Из приведённой на рис.2.14,б схемы деформации следует уравнение совместности деформаций

∆ℓ₂ = (δ – ∆ℓ₁) ∙ cos 30. (б)

3. Физическая сторона задачи. По закону Гука

,

8,16 N₂ = 2598 – 24,51 N₁. (в)

Следует отметить, что при записи уравнения совместности деформаций величину δ необходимо подставлять со знаком “+ “, т.к. знак “ - “ в таблице исходных данных – это лишь условное обозначение того обстоятельства, что длина стержня короче номинальной. В схеме деформации на рис.2.14,б и соответственно в уравнении совместности деформаций (б) это обстоятельство учтено.

4. Синтез. Решаем систему уравнений (а) и (б):

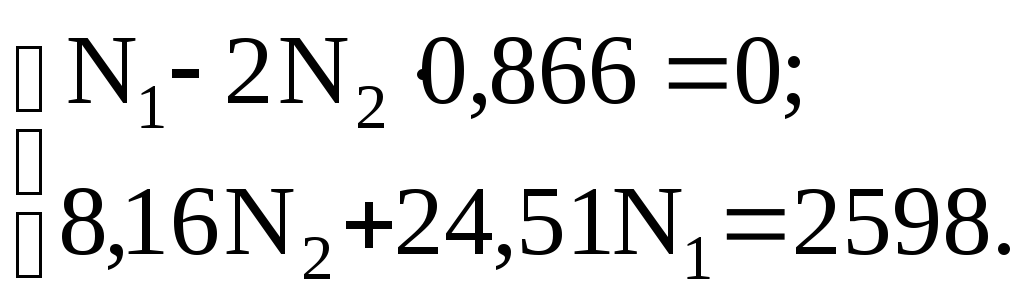
Получаем N₁ = 88,81 кН, N₂ = 51,33 кН.

5. Расчёт на прочность

, .

Напряжения меньше допускаемых (см. табл.2.1), прочность обеспечена.

На основании рассмотренных примеров можно отметить следующие особенности статически неопределимых конструкций, которыми они отличаются от статически определимых:

1. Распределение усилий между элементами статически неопределимых конструкций зависит от жёсткостей этих элементов. Если увеличить жёсткость какого- либо из них, то он примет на себя большее усилие.

2. В статически неопределимых конструкциях при изменении температуры её элементов по сравнению с температурой, при которой осуществлялась сборка конструкций, возникают усилия и напряжения.

3. В элементах статически неопределимых конструкций могут существовать усилия и напряжения при отсутствии внешней нагрузки. Эти усилия и напряжения, называемые начальными (монтажными), появляются при сборке конструкции. Начальные напряжения или создаются с определённой целью (например, затяжка болтов, прессовая посадка, предварительно напряжённый железобетон), или возникают вследствие неточного изготовления отдельных элементов конструкций.

4. В статически неопределимых конструкциях во всех элементах одновременно нельзя получить напряжения, равные допускаемым.