5.9. Касательные напряжения в полках тонкостенных профилей. Центр изгиба

Допущения, положенные в основу вывода формулы Журавского (5.27), соответствуют действительности, если ширина сечения b мала по сравнению с высотой h (размером, перпендикулярным нейтральной линии сечения).

Если сечение представляет собой тонкостенный профиль, то в полках ширина сечения значительна и картина распределения касательных напряжений существенно меняется: они становятся перпендикулярными к усилию Q (горизонтальными) и меняются по величине вдоль полки. Эти напряжения будем обозначать τ_П.

Заметим, что в полках действуют и касательные напряжения, параллельные Q. Однако эти напряжения настолько малы по сравнению с касательными напряжениями в стенке (см. график на рис.5.24) и по сравнению с τ_П, что их можно совсем не принимать во внимание.

Получим формулу для касательных напряжений τ_П в полках тонкостенных профилей, вывод проведем на примере консольной балки швеллерного сечения, нагруженной сосредоточенной силой (рис. 5.29). Так же, как и при выводе формулы Журавского, Q = const, M – линейная функция (рис.5.29,б).

Двумя близкими поперечными сечениями A₁B₁ и A₂B₂ выделим элемент балки длиной dx (рис.5.29,в). Далее отсечем часть полки m₁m₂ (рис.5.29,г), проведя линию, параллельную оси y на расстоянии z от края полки. Рассмотрим равновесие этого элемента (рис.5.29,д). В поперечных сечениях действуют нормальные напряжения σ′ и σ′′, причём σ′′ > σ′ ввиду неравенства изгибающих моментов.

Учитывая, что полка узкая (t мало по сравнению с шириной b и высотой h), примем следующие допущения:

1) нормальные напряжения σ постоянны по толщине t;

2) касательные напряжения τ_П также постоянны по толщине и зависят только от расстояния z;

3) всюду в полке τ_П параллельны нейтральной линии z.

Нормальные напряжения:

,

,

где h₁ – расстояние между осями полок, h₁ = h – t.

а б в

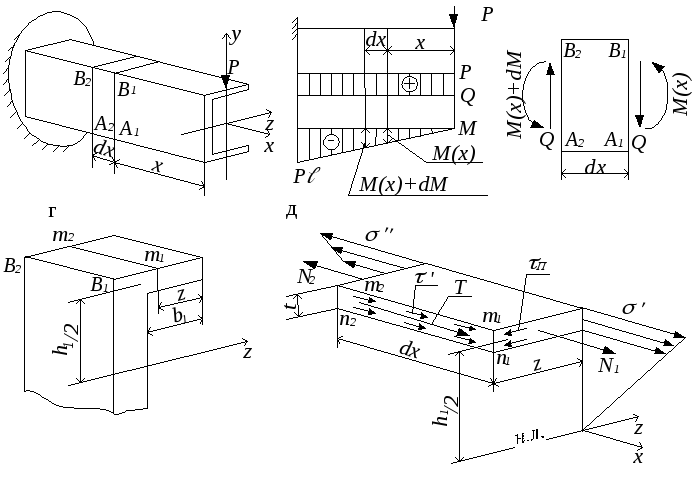
Рис.5.29

Нормальные усилия:

, . (5.44)

Ввиду того, что N₂ > N₁, равновесие рассматриваемого элемента возможно только в том случае, если по грани m₁m₂n₂n₁ будут действовать касательные напряжения τ′, равные по закону парности касательным напряжениям τ_П. Касательное усилие

Т = τ′∙ t ∙ dx = τ_П ∙ t ∙ dx. (5.45)

Уравнение равновесия рассматриваемого элемента имеет вид

 x = N₁ + T – N₂ = 0.

Подставляя N по формулам (5.44) и Т по формуле (5.45), получим

,

,

.

Учитывая, что , находим

. (5.46)

Напряжения τ_П меняются по линейному закону и достигают наибольшего значения в точке сопряжения полки со стенкой

. (5.47)

Если в формуле (5.46) числитель и знаменатель умножить на t, получим формулу, идентичную формуле Журавского

, (5.48)

где - статический момент отсечённой части полки.

Напряжения τ_П всегда образуют единый поток с касательными напряжениями τ в стенке профиля (рис.5.30,а). Последние направлены в сторону Q. Касательные напряжения в стенке и полках здесь приводятся к усилиям T_cm и T_П, показанным на рис. 5.30,б. Эти усилия создают относительно точки O, через которую проходит поперечная сила Q, крутящий момент. Открытые тонкостенные профили очень плохо сопротивляются кручению. Для исключения кручения надо, чтобы поперечная сила проходила через точку, относительно которой момент внутренних касательных усилий равнялся бы нулю. Эта точка называется центром изгиба.

а б

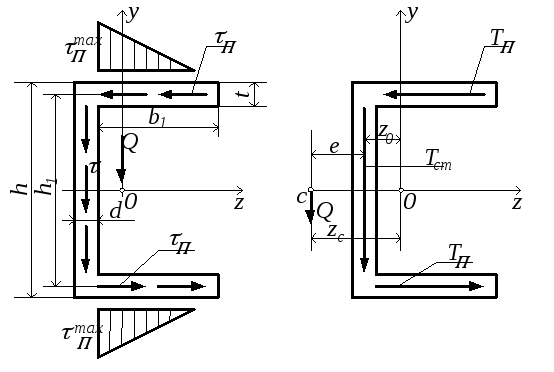
Рис.5.30

Найдём положение центра изгиба из условия равенства нулю момента внутренних касательных усилий

 М_с= – Т_cm∙e+T_П∙h₁= 0,

T_cm=Q,

T_П= площади эпюры τ_П½ ∙b₁∙t.

Подставим по формуле (5.48) и получим

,

. (5.49)

Если исходить из размеров, заданных в сортаменте, то

. (5.50)

Удобнее отсчитывать расстояние не от оси стенки, а от центра тяжести сечения

. (5.51)

Если сечение имеет две оси симметрии и силовая плоскость проходит через одну из них (например у двутавра), то в нём возникают касательные напряжения, показанные на рис.5.31,а. В силу симметрии полок относительно вертикальной оси горизонтальные усилия T_П взаимно уравновешиваются на каждой полке. Центр изгиба совпадает с центром тяжести, кручения нет.

Чтобы избежать кручения при изгибе тонкостенного несимметричного профиля (рис.5.31,б), необходимо применять симметричный профиль из двух швеллеров или выносить нагрузку из главной плоскости так, чтобы она проходила через центр изгиба (рис.5.31,в).

а б в

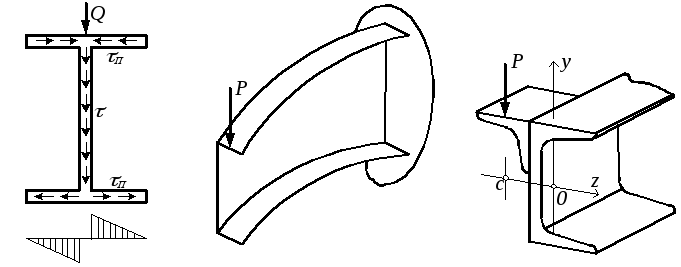
Рис.5.31