
физика акимов (АДб)
.pdf
35. Момент импульса вращающегося тела относительно оси вращения
Lz Jz ,
где ω – угловая скорость тела. 36. Для материальной точки
Lz m v r,
где r – расстояние точки от оси, относительно которой определяется момент импульса; m – масса точки; v – линейная скорость.
37. Работа постоянного момента силы Mz , действующего на вращающее тело, находится по формуле
A Mz ,
где φ – угол поворота тела.
38. Кинетическая энергия вращающегося тела
Ek Jz 2 . 2
39. Кинетическая энергия тела, катящегося по плоскости без скольжения, равна
|
|
|
Ek |
m v2 |
|
Jz 2 |
, |
||
|
|
|
|
|
|||||
|
|
|
2 |
2 |
|
|
|||
где |
|
m v2 |
кинетическая энергия поступательного движения тела; |
||||||
2 |
|||||||||
|
|
|
|
Jz 2 |
|||||
v – |
|
|
|
|
|
||||
скорость центра масс тела; |
|
|
|
кинетическая энергия |
|||||
2 |
|
||||||||
|
|
|
|
|
|
|
|||
вращательного движения тела вокруг оси, проходящей через центр инерции.
40. Закон сохранения момента импульса: если суммарный момент внешних сил относительно некоторой оси равен нулю, то момент импульса системы относительно этой оси есть величина постоянная:
Lz const .
21

3.2. Механические колебания и волны в упругих средах
1. Смещение, скорость и ускорение при гармоническом колебании:
хА cos( t ); v х А sin( t );
a х v А 2 cos( t ),
где A – амплитуда колебаний; – угловая или циклическая частота;
φ– начальная фаза.
2.Циклическая частота , период колебаний T и частота
связаны соотношением |
|
2 |
2 . |
|
|||
|
|
T |
|
3. При сложении двух одинаково направленных гармонических колебаний одинакового периода получается гармоническое колебание того же периода, амплитуда которого A и начальная фаза 0 определяются уравнениями:
А 
 А12 А22 2А1 А2 cos( 2 1);
А12 А22 2А1 А2 cos( 2 1);
tg 0 А1 sin 1 А2 sin 2 , А1 cos 1 А2 cos 2
где A1 и A2 – амплитуды складываемых колебаний; φ1 и φ2 – начальные фазы.
При сложении двух гармонических взаимно перпендикулярных колебаний одинакового периода получается гармоническое колебание следующего вида:
X2 |
|
Y2 |
|
2X Y |
cos sin2 , |
|
A2 |
A2 |
|
||||
|
|
A A |
||||
1 |
2 |
1 |
2 |
|
||
где A1 и A2 – амплитуды складываемых колебаний; φ – разность фаз обоих колебаний;
X2 |
|
Y2 |
1, |
|
π |
; |
|
A2 |
A2 |
||||||
|
|||||||
|
|
2 |
|||||
1 |
2 |
|
|
|
|
||
Y A2 X , Δφ = 0;
A1
22

Y A2 X , Δφ = .
A1
Сила, действующая на тело при свободном гармоническом колебании (квазиупругая сила),
F m a m 02 x k x,
где k m 20 – коэффициент квазиупругой силы.
4. При отсутствии сопротивления среды циклическая частота свободных колебаний ω0, называемая собственной циклической частотой, и период колебаний T равны:
|
|
|
|
k |
|
; |
|
|
Т 2 |
|
m |
. |
||||||
|
|
|
||||||||||||||||
|
|
|||||||||||||||||
|
0 |
|
|
m |
|
|
|
|
|
|
|
|
k |
|||||
5. |
Период колебаний математического маятника длиной L |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Т 2 |
|
|
L |
|
|
|
|
|||||||
|
|
|
|
|
|
g . |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
6. |
Период колебаний физического маятника |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
T 2 |
|
|
|
J |
|
, |
|
|
||||||||
|
|
m g d |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
где J – момент инерции маятника относительно оси качения; d – расстояние от оси до его центра тяжести.
7. Полная энергия тела, совершающего гармонические колебания, равна
Е m 2 A2 . 2
8. Уравнение смещения в затухающих колебаниях при наличии сил сопротивления, пропорциональных скорости (Fсопр r v, где r –
коэффициент сопротивления), имеет вид
x A0 e t sin( t 0),
где A0 e t – убывающая во времени амплитуда смещения; – коэффициент затухания; ω – циклическая частота затухающих
23

колебаний; φ0 – начальная амплитуда и фаза. Величины , ω
выражаются через параметры системы r, |
m формулами: |
||||||
|
r |
|
|
|
|||
|
; |
|
2 |
2 |
. |
||
|
|||||||
|
2m |
0 |
|
|
|||
|
|
|
|
|
|||
9.Логарифмический декремент затухания
ln A1 T ,
A2
где A1 и A2 – амплитуды двух последовательных колебаний, отстающих по времени друг от друга на период.
10. Амплитуда вынужденных колебаний
A |
|
|
h |
|
, |
|
|
|
|
|
|||
( 2 |
2) 4 2 2 |
|||||
|
|
|
|
|||
0 |
|
|
|
|||
где h – отношение амплитуды вынуждающей силы к массе тела; ω0 – собственная циклическая частота; Ω – циклическая частота вынуждающей силы.
11.Резонансная циклическая частота
рез 
 20 2 2 .
20 2 2 .
12.Уравнение плоской бегущей волны, распространяющейся со скоростью vв направлении оси Ox:
х А sin (t |
r |
) |
или х А sin( t k r), |
|
|||
|
v |
|
|
где x – смещение от положения равновесия точки, находящейся на расстоянии r от источника гармонических колебаний, характеризующихся амплитудой A, циклической частотой ω с начальной
фазой φ0 = 0; k – волновое число, |
k |
|
|
2 |
|
2 |
, |
– длина |
||
v |
|
T v |
|
|
||||||
волны. |
|
|
|
|
|
|
|
|
|
|
13. Длина волны связана с периодом колебаний T и частотой соотношениями:
v Т и |
v. |
|
|
14. Связь между разностью фаз φ двух точек бегущей волны и разностью хода r = r2 – r1 (т.е. разностью расстояний этих точек от источника колебаний):
24

2 r.
15. Уравнение стоячей волны:
y = A coskx cosωt .
16. Фазовая скорость продольных волн в тонких стержнях
v2 E ,
где E – модуль упругости; – плотность материала стержня.
3.3. Основы молекулярной физики и термодинамики
1.Количество вещества тела (системы)
N ,
NA
где N – число структурных элементов (молекул, атомов, составляющих тело); NA – постоянная Авогадро, NA = 6,02 10-23 моль-1.
2.Молярная масса вещества
Мm ,
где m – масса однородного тела; – количество вещества этого тела. 3. Относительная молекулярная масса вещества
Mr = n Ari ,
где n – число атомов i-го химического элемента, входящего в состав молекулы данного вещества; Ari – относительная атомная масса этого элемента.
4. Связь молекулярной массы M с относительной молекулярной массой вещества:
M = Mr k ,
где k = 10-3 кг/моль.
25
5. Количество вещества смеси газов:
|
2 |
|
|
; |
|
N1 |
|
N2 |
|
N3 |
|
Nn |
; |
|||||||
|
|
|
|
|
|
|||||||||||||||
1 |
3 |
|
|
|
n |
|
|
|
NA |
|
NA NA |
|
NA |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
m1 |
|
m2 |
|
m3 |
|
mn |
, |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
M1 M2 |
|
M3 |
|
|
Mn |
|
|
|
||||||||
где υi, Ni, mi, Mi – соответственно количество вещества, число молекул, масса, молярная масса i-го компонента смеси.
6. Уравнение Менделеева–Клапейрона (уравнение состояния идеального газа):
р V |
m |
R T или |
p V R T , |
|
|||
|
M |
|
|
где р – давление; V – объем; m – масса газа; M – молекулярная масса газа; R – молекулярная газовая постоянная; υ – количество вещества; T – термодинамическая температура.
7. Опытные газовые законы, являющиеся частными случаями уравнения Менделеева–Клапейрона для изопроцесса:
а) закон Бойля–Мариотта (изотермический процесс: T = const; m = const):
р V = const ,
для двух состояний газа р1 V1 = р2 V2 ;
б) закон Гей–Люссака (изобарный процесс: p = const; m = const):
|
|
V |
const , |
|||
|
|
|||||
|
|
T |
|
|
|
|
для двух состояний |
|
p1 |
|
p2 |
; |
|
T1 |
|
|||||
|
|
T2 |
||||
в) объединённый газовый закон (m = const):
р V |
const или |
p1 V1 |
|
p2 V2 |
, |
|
T1 |
|
|||
T |
|
T2 |
|||
где p1, V1, T1 – давление, объём и температура в начальном состоянии; p2, V2, T2 – те же величины в конечном состоянии.
8.Закон Дальтона, определяющий давление смеси газов:
р= p1 + p2 + p3 + …+pn ,
26

где pi – парциальные давления компонентов смеси; n – число компонентов смеси.
Парциальным давлением называется давление газа, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью.
9. Молярная масса смеси газов
M m1 m2 m3 mn ,
1 2 3 n
где mi – масса i-го компонента смеси; n – число компонентов смеси;i – количество вещества i-го компонента смеси.
10. Концентрация молекул
n N NA ,
V M
где N – число молекул, содержащихся в данной системе; ρ – плотность вещества; V – объём системы.
11. Основное уравнение кинетической теории газов:
2
р 3n n
n  ,
,
где  n
n  средняя кинетическая энергия поступательного движения молекул.
средняя кинетическая энергия поступательного движения молекул.
12. Средняя кинетическая энергия поступательного движения молекул
3
 n
n  2k T ,
2k T ,
где k – постоянная Больцмана.
13. Средняя полная кинетическая энергия молекулы
n |
|
i |
k T , |
|
|||
|
2 |
|
|
где i – число степеней свободы.
14. Зависимость давления газа от концентрации молекул и температуры:
p = n k T.
15. Скорости молекул:
27
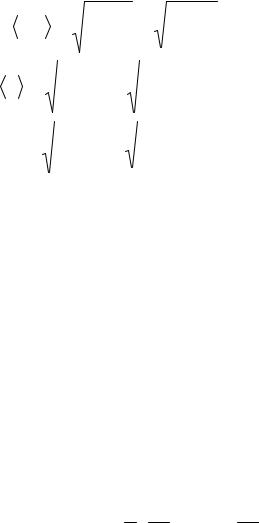
vкв |
|
|
3k T |
|
|
|
3R T |
средняя квадратичная; |
||||||||||||
|
m1 |
|
M |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
v |
|
|
8k T |
|
|
8R T |
|
средняя арифметическая; |
||||||||||||
|
|
|
|
|
|
|
|
M |
|
|||||||||||
|
|
|
|
m1 |
|
|
|
|
|
|||||||||||
vВ |
2k T |
|
|
|
|
|
2R T |
|
|
наиболее вероятная, |
||||||||||
|
|
|
|
|
M |
|||||||||||||||
|
|
|
|
|
m1 |
|
|
|
|
|
||||||||||
где m1 – масса одной молекулы.
16. Удельные теплоёмкости газа при постоянном объёме CV и постоянном давлении Cp:
С |
i R |
; |
С |
p |
|
(i 2) R |
. |
|
|
||||||
V |
2M |
|
|
2M |
|||
17. Связь между удельной c и молярной C теплоёмкостями:
с |
С |
; |
C c M . |
|
|||
|
M |
|
|
18. Уравнение Майера: |
|
||
Cp – CV = R .
19. Внутренняя энергия идеального газа
U i m R T m C T . |
|
2 M |
M V |
20. Первое начало термодинамики:
Q = U + A,
где Q – теплота, сообщённая системе (газу); U – изменение внутренней энергии системы; A – работа, совершённая системой против внешних сил.
21. Работа расширения газа:
|
|
V2 |
|
|
– в общем случае; |
|
|
А pdV |
|||
|
|
V1 |
|
|
|
|
А р(V2 |
V1) – при изобарном процессе; |
|||
A |
m |
R T ln |
V2 |
– при изотермическом процессе; |
|
|
V1 |
||||
|
M |
|
|
||
28

|
m |
|
|
|
|
|
RT |
|
m |
|
V |
|
1 |
|
|||
A U |
|
C |
T |
или |
A |
1 |
|
|
|
1 |
1 |
|
|
|
|||
|
|
|
|
||||||||||||||
M |
V |
|
|
|
|
1 M |
|
|
|
|
|
||||||
|
|
|
|
V2 |
|
|
|||||||||||
|
|
|
|
|
|
Ср |
|
|
|
|
|
|
|
|
|
|
|
при адиабатном процессе, где |
|
показатель адиабаты. |
|
||||||||||||||
|
|
||||||||||||||||
СV
22. Уравнение Пуассона. Связывающие параметры идеального газа при адиабатном процессе:
|
|
Т |
2 |
|
|
V1 |
1 |
|
p |
|
V |
|
|
Т |
|
|
V |
1/ |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
2 |
|
|
1 |
|
|
р V |
const; Т |
|
V |
|
; |
|
; |
|
|
|
. |
|||||||||||||
|
1 |
|
|
2 |
|
p |
V |
|
|
Т |
|
V |
|
|||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
1 |
|
|
2 |
|
|
||||
23.Термодинамический КПД цикла
Q1 Q2 ,
Q1
где Q1 – теплота, полученная рабочим телом от теплоотдатчика; Q2 – теплота, переданная рабочим телом теплоприёмнику.
24.Теплодинамический КПД цикла Карно
Q1 Q2 T1 T2 ,
Q1 T1
где T1 и T2 – термодинамические температуры теплоотдатчика и теплоприёмника.
3.4. Электростатика. Постоянный ток
1. Закона Кулона:
F |
Q1 Q2 |
, |
|
4 0 r2 |
|||
|
|
где F – сила взаимодействия точечных зарядов Q1 и Q2; r – расстояние между зарядами; ε – диэлектрическая проницаемость; ε0 – электрическая постоянная.
2. Напряжённость электрического поля и потенциал:
|
F |
|
Ep |
|
|
E |
|
; |
|
|
, |
|
Q |
||||
|
Q |
|
|
||
29

где Ep – потенциальная энергия точечного положительного заряда Q, находящегося в данной точке поля (при условии, что потенциальная энергия заряда, удалённого в бесконечность, равна нулю).
3. Сила, действующая на точечный заряд, находящийся в электрическом поле, и потенциальная энергия этого заряда:
F Q E; |
Ep Q . |
4. Напряжённость и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции электрических полей):
|
n |
n |
E Ei ; |
i , |
|
|
i 1 |
i 1 |
где Ei и φi – напряжённость и потенциал в данной точке поля, создаваемого i-м зарядом.
5. Напряжённость и потенциал поля, создаваемого точечным зарядом:
Е |
Q |
; |
|
Q |
, |
4 0 r2 |
4 0 r |
где r – расстояние от заряда Q до точки, в которой определяются напряжённость и потенциал.
6. Напряжённость и потенциал поля, создаваемого проводящей заряженной сферой радиусом R на расстояние r от центра сферы:
а) |
Е 0, |
|
|
Q |
|
|
(при r R); |
||||||
4 0 R |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||
б) |
Е |
|
Q |
|
|
|
, |
|
|
Q |
(при r = R); |
||
4 0 R2 |
|
|
4 0 R |
||||||||||
в) |
Е |
|
|
Q |
|
|
, |
|
|
Q |
(при r R), |
||
|
4 0 r2 |
|
|
4 0 r |
|
||||||||
где Q – заряд сферы.
7.Линейная плотность заряда
Q . l
8.Поверхностная плотность заряда
Q .
S
30
