Часть 3 Графы

ЗАДАНИЕ

Вариант 7
Задание 1. Определить кратчайшие пути от вершины 1 до всех остальных вершин графа, используя алгоритм Дейкстры. Построить дерево кратчайших путей. Отрицательные длины в матрице заменить положительными (матрица 1).
Задание 2. Определить кратчайшие пути от вершины 1 до всех остальных вершин графа, пользуясь алгоритмом Беллмана. Построить дерево кратчайших путей (матрица 1).
																																						Матрица 1
				1				2					3						4					5						6						7					8						9						10
	1			−				−					−						−					2						5						3					−						−						−
	2			7				−					5						−					10						5						−					−						-1						−
	3			7				−					−						−					−						6						2					−						−						10
	4			−				6					8						−					−						−						−					7						2						−
	5			3				8					−						1					−						−						7					−						10						7
	6			2				−					10						-2					6						−						−					3						−						−
	7			−				−					9						7					−						−						−					−						−						−
	8			−				3					−						7					−						−						2					−						−						9
	9			−				−					7						−					6						−						-1					−						−						−
	10			1				−					−						−					−						8						8					−						6						−
Задание 3. Определить кратчайшие пути между всеми парами вершин графа, используя алгоритм Флойда. Построить деревья кратчайших путей (матрица 2).
																																Матрица 2
										1								2									3								4									5
			1							−								−									-3								−									8
			2							−								−									9								7									−
			3							−								9									−								3									8
			4							-3								1									−								−									−
			5							1								−									1								10									−

Задание 4. Отыскать гамильтонов контур наименьшей длины, пользуясь алгоритмом ветвей и границ (матрица 3).

													Матрица 3
		1			2			3			4			5	6	7
1		∞			13			6			12			9	10	5
2		14			∞			10			11			10	5	9
3		13			7			∞			7			15	8	14
4		8			6			10			∞			4	12	3
5		8			7			9			14			∞	3	7
6		5			3			15			1			10	∞	12
7		5			3			15			8			9	15	∞

Задание 5. В графе на рис. 1 найти центр, главный центр, абсолютный центр, медиану, главную медиану, абсолютную медиану.

РЕШЕНИЕ

Задание 1.

1.Положим и будем считать эту метку постоянной.

2.

3.

4.

5.

6.

7.

8.

_{9. Из вершины 10 можно попасть в вершины 1,6,7,9, но для них уже найдены постоянные кратчайшие пути, переходим к следующей метке.}

10.

11.

	1	2	3	4	5	6	7	8	9	10
1											p=1
2					2+	5	3				p=5
3		10		3+	2+	5	3		12	9	p=4
4		9	11	3+	2+	5	3+	10	5	9	p=7
5		9	11	3+	2+	5	3+	10	5+	9	p=9
6		9	11	3+	2+	5+	3+	10	5+	9	p=6
7		9	11	3+	2+	5+	3+	8+	5+	9	p=8
8		9	11	3+	2+	5+	3+	8+	5+	9+	p=10
9		9+	11	3+	2+	5+	3+	8+	5+	9+	p=2
10		9+	11+	3+	2+	5+	3+	8+	5+	9+	p=3

Построим дерево кратчайших путей

Задание 2.

	1	2	3	4	5	6	7	8	9	10
1	0	∞	∞		2	5
2	0	10	12	3	2	5		8	12	9
3	0	9			2	5
4	0			3	2	5

;;;;

;;;;;;.

;

;;;.

Построим дерево кратчайших путей

Задание 3.

	1	2	3	4	5
1	0	7	∞	2	∞
2	∞	0	7	9	6
3	5	12	0	7	-1
4	∞	1	6	0	∞
5	5	-2	∞	7	0

_.

	1	2	3	4	5
1	0	7	14	2	13
2	∞	0	7	9	6
3	5	12	0	7	-1
4	∞	1	6	0	7
5	5	-2	5	7	0

_{; ;.}

	1	2	3	4	5
1	0	7	14	2	12
2	12	0	7	9	6
3	5	12	0	7	-1
4	11	1	6	0	5
5	5	-2	5	7	0

_;;;;;.

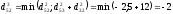	1	2	3	4	5
1	0	7	8	2	7
2	12	0	7	9	6
3	5	8	0	7	-1
4	11	1	6	0	5
5	5	-2	5	7	0

_{; ;;.}

	1	2	3	4	5
1	0	3	8	2	7
2	11	0	7	9	6
3	4	-3	0	6	-1
4	10	1	6	0	5
5	5	-2	5	7	0

_{; ;}

Построим деревья кратчайших путей

Задание 4.

Шаг 1

	1	2	3	4	5	6	7
1		13	6	12	9	10	5	5
2	14		10	11	10	5	9	5
3	13	7		7	15	8	14	7
4	8	6	10		4	12	3	3
5	8	7	9	14		3	7	3
6	5	3	15	1	10		12	1
7	5	3	15	8	9	15		3

Шаг 2

	1	2	3	4	5	6	7
1		8	1	7	4	5	0
2	9		5	6	5	0	4
3	6	0		0	8	1	7
4	5	3	7		1	9	0
5	5	4	6	11		0	4
6	4	2	14	0	9		11
7	2	0	12	5	6	12
	2		1		1

Нижняя граница: 5+5+7+3+3+1+3+2+1+1=31

Шаг 3

	1	2	3	4	5	6	7
1		8	04	7	3	5
2	7		4	6	4	04	4
3	4	00		00	7	1	7
4	3	3	6		03	9
5	3	4	5	11		03	4
6	2	2	13	02	8		11
7	02	00	11	5	5	12

Шаг 4

	1	2	4	5	6	7
2	7		6	4	04	4
3		00	00	7	1	7
4	3	3		04	9
5	3	4	11		03	4
6	2	2	02	8		11
7	02	00	5	5	12

Не до приводится

Шаг 5

	1	2	4	5	7
3		0	0	7	7
4	3	3		0
5	3	4	11		4	3
6	2		0	8	11
7	0	0	5	5

Доприводим 5 строку на 3

Шаг 6

	1	2	4	5	7
3		00	00	7	7
4	3	3		05
5	01	1	8		1
6	2		02	8	11
7	00	00	5	5

Шаг 7

	1	2	4	7
3			0
5	0	1		1
6	2		0	11
7			5
				1

Доприводим 7 столбец на единицу

Шаг 8

	1	2	4	7
3			00
5	00	1		06
6	2		02	10
7			5

Шаг 9

	1	2	4
3			00
6	2
7

Не доприводим

Шаг 10

	1	3
2
6

Гамильтонов контур: 4---5---7---1---3---2---6---4(4+7+5+6+7+5+1=35)

Задание 5.

Рассмотрим граф на рис. 1 с матрицей D (табл.1)

Найдем внешний центр.

Таблица 1

j i	1	2	3	4	∑
1	0	10	4	19	33
2	10	0	9	9	28
3	4	9	0	18	31
4	7	15	6	0	28
∑	21	34	19	46

D =

; ;

;;

Внешний центр графа – это вершина 2. В табл. 1 числа выделены желтым.

Найдем внутренний центр для графа на рис. 1

; ;

; ;

;

Внутренний центр для графа – вершина 2. В табл.1 числа выделены курсивом с подчеркиванием.

Найдем внешнюю медиану для графа на рис. 1

;;

;;

=28,внешняя медиана – вершины 2 и 4. Число 9 выделено в табл. 1 жирным шрифтом и желтым цветом.

Найдем внутреннюю медиану для графа на рис. 1

;;

;;

=19, внутренняя медиана – вершина 3. Число 9 выделено в табл. 1 жирным шрифтом и желтым цветом.

Таблица 2

	1	10	4	11,5	25	19	26	95,5
D1 =	2	10	11,5	9	15	9	16	70,5
	3	11,5	4	9	24	18	25	91,5
	4	16	8,5	15	6	24	7	76,5

Найдем Главный внешний центр графа таблица 2

В этом графе главный внешний центр – вершина 2. Число 16 выделено жирным курсивом.

Найдем Главную внешнюю медиану графа

min(95,5;70,5;91,5;76,5)=70,5.

Главная внешняя медиана – это вершина 2. Число 70,5 выделено в табл. 2 жирным шрифтом.

Таблица 3

D2 =	Вершина Ребро(дуга)	1	2	3	4
		10	10	11,5	19
		4	11,5	4	20,5
		11,5	9	9	18
		10	15	6	24
		16	24	15	9
		7	17	11	26
	∑	58,5	86,5	56,5	116,5

Найдем главный внутренний центр графа таблица 3

Min(16,24,15,26)=15

В графе один внутренний центр – вершина 3. Число 15 в табл. 3 выделено также курсивом.

Найдем главную внутреннюю медиану графа таблица 3

Min(58,5;86,5;56,5;116,5)=56,5;главная внутренняя медиана – это вершина 3. Число 56,5 выделено в табл. 3 жирным шрифтом.

Найдем внешний абсолютный центр

Построим графики расстояний точка-вершина для всех точек ребра (1,2) до всех вершин графа.

Минимум максимальных расстояний точка-вершина для точек ребра (1,2) равен 9,5 и достигается при f =

Построим графики расстояний точка-вершина для всех точек ребра (1,3) до всех вершин графа.

Минимум максимальных расстояний точка-вершина для точек ребра (1,3) равен 18 и достигается при f = 1, то есть в вершине 3.

Построим графики расстояний точка-вершина для всех точек ребра (1,4) до всех вершин графа.

Минимум максимальных расстояний точка-вершина для точек ребра (2,3) равен 10 и достигается при f = 0, т. е. в вершине 2

Таблица 4

Ребро
(1, 2)	9.5	19/20
(1,3)	10	0(вершина 3)
(2,3)	18	1(вершина 2)
Внешний центр		Вершина 2

Абсолютным внешним центром этого графа является 19/20-точка ребра

(1, 2); абсолютный минимум расстояний точка-вершина равен 9.5

Абсолютная внешняя медиана совпадет с внешней медианой, это вершины 2 и 4

Найдем абсолютный внутренний центр графа.

Рассмотрим ребро (1, 2).

Минимум максимальных расстояний точка-вершина для точек ребра (1,2) равен 8,5 и достигается при f =

Рассмотрим ребро (1, 3).

Минимум максимальных расстояний точка-вершина для точек ребра (1,3) равен 9 и достигается при f = 1, т.е. в вершине 3.

Рассмотрим ребро (2,3).

Минимум максимальных расстояний точка-вершина для точек ребра (2,3) равен 7,5 и достигается при f =

Ребро
(1, 2)	8,5	3/20
(1,3)	9	1(вершина 1)
(2,3)	7,5	15/18
Внутренний центр		Вершина (2)

Абсолютным внутренним центром этого графа является 15/18-точка ребра

(2, 3); абсолютный минимум расстояний точка-вершина равен 7,5.

Абсолютная внутреняя медиана совпадет с внутренней медианой, это вершина 3