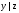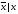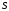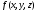хМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Сибирская государственная автомобильно-дорожная академия
(СибАДИ)»
Факультет Информационные системы в управлении (ИСУ)
Специальность Автоматизированные системы обработки информации и управления (АСОИУ)
Кафедра Компьютерные информационные автоматизированные системы (КИАС)
Курсовая работа по дисциплине
Математическая логика и теория алгоритмов
Тема Алгоритмы дискретной математики
Выполнил: студент гр.АС-10И2
Курганов И.Д.
Проверил: преподаватель
Палий И.А.
Омск – 2012г.
Содержание
Введение
Часть 1. Логические функции (Функции алгебры логики).
ЗАДАНИЕ
Логическая функция A двух переменных.
Расставить скобки в формуле своего варианта в соответствии со старшинством логических операций, так чтобы сделать явной последовательность вычисления значений логической функции. Составить таблицу истинности функции. Применяя равносильные преобразования, построить ДНФ и СДНФ этой функции.
Логическая функция B двух переменных.
Расставить скобки в формуле своего варианта в соответствии со старшинством логических операций, так чтобы сделать явной последовательность вычисления значений логической функции. Составить таблицу истинности. Применяя равносильные преобразования, построить КНФ и СКНФ этой функции.
Логическая функция C трех переменных.
Расставить скобки в формуле своего варианта в соответствии со старшинством логических операций, так чтобы сделать явной последовательность вычисления значений логической функции. Составить таблицу истинности функции. Применяя равносильные преобразования, построить ДНФ и СДНФ, КНФ и СКНФ, СПНФ этой функции.
Логическая функция D трех переменных.
Расставить скобки в формуле своего варианта в соответствии со старшинством логических операций, так чтобы сделать явной последовательность вычисления значений логической функции. Составить таблицу истинности функции. Определить, к каким классам Поста принадлежит эта функция, дать подробные объяснения.
Логическая функция E четырех переменных.
Построить минимальные ДНФ и КНФ функции E четырех переменных своего варианта, заданной вектором своих значений. Воспользоваться двумя алгоритмами: методом Квайна и картами Карно. Определить, к каким классам Поста принадлежит эта функция, дать подробные объяснения.
Вариант 7
Логическая функция A двух переменных 1
Построим таблицу истинности заданной функции:
|
x |
y |
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
0 |
1 |
1 |
Применяя равносильные преобразования, попытаемся построить ДНФ и СДНФ этой функции:
1)

2)
ДНФ:

Построим СДНФ:
 :
:
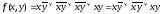
СДНФ:

Логическая функция B двух переменных
Построим таблицу истинности заданной функции:
|
x |
y |
|
|
|
|
f |
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
1 |
1 |
КНФ и СКНФ для этой функции равны единице, так как эта функция является "константой 1".
КНФ = СКНФ =1
Логическая функция C трех переменных
Построим таблицу истинности заданной функции:
|
x |
y |
z |
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
1 |
1 |
0 |
Применяя равносильные преобразования, попытаемся построить ДНФ и СДНФ этой функции:
1)

2)

3)
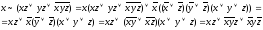
4)
 -ДНФ
-ДНФ
СДНФ:

СКНФ:
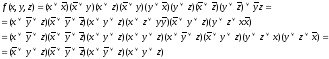
СПНФ:
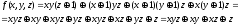 Логическая
функция D
трех переменных
Логическая
функция D
трех переменных
Построим таблицу истинности заданной функции:
|
x |
y |
z |
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
Проверим функцию на линейность

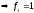
|
f |
f1 |
|
0 |
1 |
|
1 |
1 |
|
0 |
1 |
|
1 |
1 |
|
1 |
1 |
|
1 |
1 |
|
0 |
1 |
|
0 |
1 |

Проверим функцию на монотонность
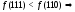
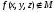
111>110
Проверим функцию на сохранение нуля

Проверим функцию на сохранение единицы

Проверим функцию на самодвойственность
|
f |
f* |
|
1 |
1 |
|
1 |
0 |
|
1 |
0 |
|
0 |
0 |
|
1 |
1 |
|
1 |
0 |
|
1 |
0 |
|
0 |
0 |

Построим таблицу поста для этой функции
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Логическая функция E четырех переменных
0111010000101101
Восстановим таблицу истинности функции по её вектору значения:
|
X1 |
X2 |
X3 |
X4 |
F(x1,x2,x3,x4) |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
Выпишем СДНФ и СКНФ для этой функции
СДНФ:

СКНФ :

Составим карту Карно для ДНФ
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
1 |
|
1 |
|
|
|
|
|
1 |
1 |
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
Минимальная ДНФ:

Составим карту Карно для КНФ
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
|
|
|
|
0 |
|
|
|
|
0 |
0 |
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
Минимальная КНФ:

Минимизация по методу Квайна для ДНФ
Выпишем двоичные наборы на которых функция равна 1и рассортируем их в столбцы по количеству единиц:
|
|
0011 |
|
|
|
0001 |
1010 |
1101 |
1111 |
|
0010 |
0101 |
|
|
|
|
1100 |
|
|
После проведенных склеек рассортируем полученные наборы по положению прочерка:
|
_101 |
0_01 |
00_1 |
001_ |
|
_010 |
|
11_1 |
110_ |
Выполнить дополнительные склейки нельзя.
Получим 7 двоичных наборов:
_010, _101, 0_01, 00_1, 11_1, 001_,110_
|
|
0001 |
0011 |
1010 |
1101 |
0010 |
0101 |
1100 |
1111 |
|
_010+ |
|
|
1+ |
|
1+ |
|
|
|
|
_101˅ |
|
|
|
1˅ |
|
1˅ |
|
|
|
0_01^ |
1^ |
|
|
|
|
1^ |
|
|
|
00_1˅ |
1˅ |
1˅ |
|
|
|
|
|
|
|
11_1+ |
|
|
|
1+ |
|
|
|
1+ |
|
001_^ |
|
1^ |
|
|
1^ |
|
|
|
|
110_ |
|
|
|
1+ |
|
|
1+ |
|
Ядро функции: { }
}
 -
минимальные
ДНФ
-
минимальные
ДНФ
Минимизация по методу Квайна для КНФ
Выпишем двоичные наборы на которых функция равна 0 и рассортируем их в столбцы по количеству нулей:
|
0111 |
0110 |
0100 |
0000 |
|
1110 |
1001 |
1000 |
|
|
1011 |
|
|
|
После проведенных склеек получим :
|
_110 |
0_00 |
10_1 |
011_ |
|
_000 |
|
01_0 |
100_ |
Выполнить дополнительные склейки нельзя.
Получим 7 двоичных наборов:
_110, _000, 0_00, 10_1, 01_0, 011_,100_
|
|
0000 |
0100 |
0110 |
0111 |
1000 |
1001 |
1011 |
1110 |
|
_110+ |
|
|
0+ |
|
|
|
|
0+ |
|
_000 |
0˅ |
|
|
|
0˅ |
|
|
|
|
0_00 |
0^ |
0^ |
|
|
|
|
|
|
|
10_1+ |
|
|
|
|
|
0+ |
0+ |
|
|
01_0 |
|
0˅ |
0˅ |
|
|
|
|
|
|
011_+ |
|
|
|
0+ |
|
|
|
|
|
100_ |
|
|
0^ |
|
0^ |
|
|
|
Ядро функции: { }
}
В результате получим:
 -
минимальная
КНФ
-
минимальная
КНФ
Определим принадлежность функции к основным классам поста:
Проверим функцию на линейность


|
X1 |
X2 |
X3 |
X4 |
f |
f1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
1 |
1 |
|
0 |
0 |
1 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
0 |

Проверим функцию на монотонность


1011>1010
Проверим функцию на сохранение нуля

Проверим функцию на сохранение единицы

Проверим функцию на самодвойственность
|
f |
f1 |
|
0 |
0 |
|
1 |
1 |
|
1 |
0 |
|
1 |
0 |
|
0 |
1 |
|
1 |
0 |
|
0 |
1 |
|
0 |
1 |
|
0 |
1 |
|
0 |
1 |
|
1 |
0 |
|
0 |
1 |
|
1 |
0 |
|
1 |
0 |
|
0 |
0 |
|
1 |
1 |

Построим таблицу поста для этой функции
|
|
|
|
|
|
|
|
|
+ |
+ |
|
|
|