
Метод от противного:
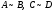 ╞
╞
Предположим,
что
 = 0. Это значит, что
= 0. Это значит, что =0,
а
=0,
а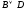 =1
или
=1
или =1
, а
=1
, а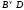 =0.
=0.
Если
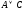 =0
следовательноA=C=0.
=0
следовательноA=C=0.
Если
В=1 и D=1,
тогда
 =0,
=0,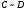 =0.
=0.
Если
B=0
и D=1,
тогда
 =0.
=0.
Если
В=1 и D=0,
тогда
 =0.
=0.
Если
 =0
, тогдаB=0
и D=0.
=0
, тогдаB=0
и D=0.
Предположим,
что А=С=1, тогда А=В=0 и
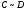 =0.
=0.
Теперь
предположим, что А=1, С=0, тогда
 =0.
=0.
Теперь
предположим, что А=0, С=1, тогда
 =0.
=0.
Исходя
из этого можно сделать вывод, что формула
 =0,
а
=0,
а =1
является логическим следствием
=1
является логическим следствием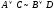 .
.
 ╞
╞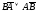 .
.
Предположим,
что
 =0
, это значит что эти обе части равны 0.
=0
, это значит что эти обе части равны 0.
Рассмотрим
такой вариант, что В=0, а
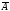 =1,
тоесть тоже самое что А=0 и В=0, тогда из
=1,
тоесть тоже самое что А=0 и В=0, тогда из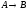 =1,
=1,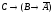 =1,
=1, ,
тоесть С=0 либо С=1.
,
тоесть С=0 либо С=1.
Если
С=0, то из
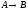 =1.
=1.
Если
С=1, то из
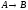 =1.
=1.
Мы
нашли такой вариант, при котором все
посылки истинны, а заключение ложно,
тоесть формула
 не является логическим следствием
не является логическим следствием .
.
Задание 2. Ввести необходимые обозначения и записать каждое из высказываний как формулу исчисления предикатов. Обосновать справедливость (ложность) заключения при помощи диаграмм Эйлера-Венна.
Некоторые писатели – женщины. Все женщины любят цветы. Следовательно, среди тех, кто любит цветы, есть писатели.
Решение:
А(х) = «х – женщина»
В(х) = «х любит цветы»
С(х) = «х – писатель»
Некоторые писатели женщины
(
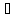 х)
( А(х) & С(х) ) 1
х)
( А(х) & С(х) ) 1
( х)
( А(х)
х)
( А(х) В(х) ) 2
В(х) ) 2
( )
( В(х) & С(х) ) 3
)
( В(х) & С(х) ) 3
( ( А(х) & С(х) ), (
( А(х) & С(х) ), (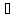 х)
( А(х)
х)
( А(х) В(х) )
В(х) ) (
( )
( В(х) & С(х) )
)
( В(х) & С(х) )
А – множество женщин
В – множество любителей цветов
С – множество писателей
а
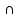 с
с

а
 в
в
в
 с
с
в
с
а
Задание
3.
Пусть предметная область
 ,
, «x
< y».
Рассмотреть все варианты одновременной
квантификации переменных двухместного
предиката
«x
< y».
Рассмотреть все варианты одновременной
квантификации переменных двухместного
предиката
 .
Определить истинность получаемых
выражений.
.
Определить истинность получаемых
выражений.
Q(x,y) = x < y
(
 (
(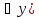 Q(x,y)
= Л. «Какой бы мы не взяли х, любой у будет
больше х» = Ложь
Q(x,y)
= Л. «Какой бы мы не взяли х, любой у будет
больше х» = Ложь Q(x,y)
= «Найдется х, что для него найдется у,
такой что у > х» = Истина.
Q(x,y)
= «Найдется х, что для него найдется у,
такой что у > х» = Истина.(
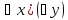 Q(x,y)
= «Для любого х, найдется у > х» = Истина.
Q(x,y)
= «Для любого х, найдется у > х» = Истина.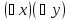 Q(x,y)
= «Найдется х, что любой у будет больше
х» = Ложь.
Q(x,y)
= «Найдется х, что любой у будет больше
х» = Ложь.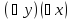 Q(x,y)
= «Для любого у, найдется х меньше у» =
Истина.
Q(x,y)
= «Для любого у, найдется х меньше у» =
Истина. (
(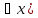 Q(x,y)
= «Найдется у, больший любого х» = Ложь.
Q(x,y)
= «Найдется у, больший любого х» = Ложь.
Глава 3. Задание по программированию Программирование алгоритма дискретной математики
Задание:
Общие положения. При выполнении задания необходимо
1. Подробно описать алгоритм.
2. Подробно описать программу, реализующую алгоритм: типы и структуры данных, блок-схему программы и т.п.
3. Привести листинг программы.
4. Привести результаты решения не мене трех тестовых примеров с различными исходными данными.
Индивидуальное задание(вариант 7):
Квадратная подматрица. Вводится матрица a(m,n) из 0 и 1. Найти в ней квадратную подматрицу из одних единиц максимального размера.
Блок-схема программы:



Листинг программы:
#include <stdlib>
#include <stdio>
#include "time.h"
#include "conio.h"
#include "iostream.h"
int TestRectangle(bool **array, int i_begin, int j_begin, int i_end, int j_end) {
for (int i = i_begin; i < i_end; ++i)
for (int j = j_begin; j < j_end; ++j)
if (array[i][j]==0)
return -1;
if((i_end - i_begin) == (j_end - j_begin))
return ((i_end - i_begin) * (j_end - j_begin));
else return -1;
}
int main(int argc, char *argv[]) {
srand(time(NULL));
int farm_width = 10;
int farm_height = 10;
bool **array = new bool*[farm_height];
for (int i = 0; i < farm_height; ++i) {
array[i] = new bool[farm_width];
for (int j = 0; j < farm_width; ++j)
printf("%2d", array[i][j] = rand() % 2);
printf("\n");
}
int max_i_begin = 0, max_j_begin = 0, max_i_end = 0, max_j_end = 0;
int max_area = 1;
for (int i_begin = 0; i_begin < farm_height; ++i_begin)
for (int j_begin = 0; j_begin < farm_width; ++j_begin)
for (int i_end = i_begin; i_end <= farm_height; ++i_end)
for (int j_end = j_begin; j_end <= farm_width; ++j_end) {
int this_area = TestRectangle(array,
i_begin, j_begin, i_end, j_end);
if (this_area > max_area) {
max_area = this_area;
max_i_begin = i_begin;
max_i_end = i_end;
max_j_begin = j_begin;
max_j_end = j_end;
}
}
printf("Max area: %d. (%d, %d) - (%d, %d) [(y1, x1) - (y2 - x2)]\n", max_area, max_i_begin + 1, max_j_begin + 1, max_i_end, max_j_end);getch();
for (int i = 0; i < farm_height; ++i)
delete [] array[i];
delete [] array;
return 0;
}
