
- •Пояснительная записка
- •Задание на курсовую работу по дисциплине «Теория вероятностей и математическая статистика»
- •1.Упорядочить выборку (все её элементы распределить по возрастанию)
- •2. Построить статистический (вариционный) ряд.
- •3. Найти точечные оценки , , асимметрии,эксцесс.
- •4. Определение параметров распределения, используя метод моментов и наибольшего правдоподобия.
- •6. Проверка гипотезы с использованием критерия Пирсона.
- •Список источников.
6. Проверка гипотезы с использованием критерия Пирсона.
Данный
критерий позволит сделать вывод о виде
распределения случайной величины в
нашем вариационном ряду. Пусть
 -
гипотеза о том, что случайная величина
Х в нашем вариационном ряду подчиняется
нормальному закону распределения. Для
подтверждения или опровержения данной
гипотезы сравним наблюдаемое значение
коэффициента Пирсона (коэффициент для
нашего вариационного ряда) с критическим
(табличным) его значением на заданном
уровне значимости
-
гипотеза о том, что случайная величина
Х в нашем вариационном ряду подчиняется
нормальному закону распределения. Для
подтверждения или опровержения данной
гипотезы сравним наблюдаемое значение
коэффициента Пирсона (коэффициент для
нашего вариационного ряда) с критическим
(табличным) его значением на заданном
уровне значимости
![]() .
.
|
|
0,201744 |
0,988804 |
1,747440 |
2,500804 |
3,261805 |
4,034272 |
4,800700 |
5,735250 |
|
0,988804 |
1,747440 |
2,500804 |
3,261805 |
4,034272 |
4,800700 |
5,735250 |
6,670003 | |
|
|
18 |
20 |
35 |
47 |
31 |
26 |
16 |
7 |
|
|
0,09 |
0,1 |
0,175 |
0,235 |
0,155 |
0,13 |
0,08 |
0,035 |
Для
расчета коэффициента Пирсона нам
необходимы эмпирические ( )
и теоретические (
)
и теоретические ( частоты.
Т.к. эмпирические были уже нами ранее
рассчитаны, подсчитаем теоретические.
Для этого необходимы значения вероятностей
,с которыми случайная величина Х попадает
в каждый из 9 интервалов нашего
вариационного ряда. Для расчета
вероятностей воспользуемся формулой
Муавра- Лапласа):
частоты.
Т.к. эмпирические были уже нами ранее
рассчитаны, подсчитаем теоретические.
Для этого необходимы значения вероятностей
,с которыми случайная величина Х попадает
в каждый из 9 интервалов нашего
вариационного ряда. Для расчета
вероятностей воспользуемся формулой
Муавра- Лапласа):

Рассчитаем значение функции Муавра-Лапласса на границах каждого интервала по формуле
 (начальное и конечное значение Z
примем равные
(начальное и конечное значение Z
примем равные
 , т.к. данные значения нашей совокупности
являются выборочными) инайдем
вероятности, с которыми случайная
величина Х попадает в каждый интервал
и подсчитаем теоретические частоты.
(Расчет вероятностей производится с
использованием таблицы значений функции
Муавра- Лапласа):
, т.к. данные значения нашей совокупности
являются выборочными) инайдем
вероятности, с которыми случайная
величина Х попадает в каждый интервал
и подсчитаем теоретические частоты.
(Расчет вероятностей производится с
использованием таблицы значений функции
Муавра- Лапласа):
|
|
|
|
|
|
|
|
|
|
0,201744 |
0,988804 |
|
-1,47124 |
-1 |
-0,899845 |
0,100155 |
20,031 |
|
0,988804 |
1,747440 |
-1,47124 |
-0,91799 |
-0,899845 |
-0,77628 |
0,123565 |
24,713 |
|
1,747440 |
2,500804 |
-0,91799 |
-0,36858 |
-0,77628 |
-0,61254 |
0,16374 |
32,748 |
|
2,500804 |
3,261805 |
-0,36858 |
0,186395 |
-0,61254 |
-0,40877 |
0,20377 |
40,754 |
|
3,261805 |
4,034272 |
0,186395 |
0,749736 |
-0,40877 |
-0,266745 |
0,142025 |
28,405 |
|
4,034272 |
4,800700 |
0,749736 |
1,308673 |
-0,266745 |
-0,143115 |
0,12363 |
24,726 |
|
4,800700 |
5,735250 |
1,308673 |
1,990217 |
-0,143115 |
-0,046235 |
0,09688 |
19,376 |
|
5,735250 |
6,670003 |
1,990217 |
|
-0,046235 |
0 |
0,046235 |
9,247 |
|
|
|
|
|
|
|
|
|
2.
Определим меру расхождения эмпирических
( и теоретических (
и теоретических ( частот
(значение коэффициента
частот
(значение коэффициента
 по
формуле:
по
формуле:
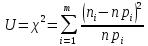
|
|
|
|
|
|
20,031 |
18 |
2,031 |
0,205929 |
|
24,713 |
20 |
4,713 |
0,898813 |
|
32,748 |
35 |
-2,252 |
0,154865 |
|
40,754 |
47 |
-6,246 |
0,957268 |
|
28,405 |
31 |
-2,595 |
0,237072 |
|
24,726 |
26 |
-1,274 |
0,065642 |
|
19,376 |
16 |
3,376 |
0,588221 |
|
9,247 |
7 |
2,247 |
0,546016 |
|
200 |
|
|
|
Отсюда следует, что X2наблюд = 3,653826
4. Сравним полученное наблюдаемое значение коэффициента с критическим значением на заданном уровне.
Для
этого воспользуемся таблицей значений
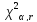 Пирсона. Число степеней свободы для
данного коэффициентаk
= m
– r
= 8 – 2 = 6
Пирсона. Число степеней свободы для
данного коэффициентаk
= m
– r
= 8 – 2 = 6 ,
гдеm-число
интервалов нашего вариационного ряда,
r-
число переменных, которыми мы описывали
наш ряд( мат.ожидание и дисперсия).
,
гдеm-число
интервалов нашего вариационного ряда,
r-
число переменных, которыми мы описывали
наш ряд( мат.ожидание и дисперсия).
X2критич = 16,8
Т.к. X2наблюд < X2критич , то оснований отвергать гипотезу о нормальности распределения данного вариационного ряда нет! Значит гипотеза не противоречит опытным данным.






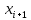

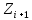


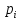 =
=






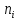



 3,653826
3,653826