2. Построить статистический (вариционный) ряд.
Оформим статистический ряд с помощью полигона
Строим таблицу:
|
X |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
|
5 |
19 |
27 |
34 |
39 |
34 |
19 |
13 |
7 |
2 |
1 |
|
P* |
2,5 |
9,5 |
13,5 |
17 |
19,5 |
17 |
9,5 |
6,5 |
3,5 |
1 |
0,5 |
Где: X –вероятностные значения x;
-
число попаданий в заданный интервал;
-
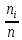- вероятность появления числа
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
F(x) |
0 |
0,025 |
0,12 |
0,255 |
0,425 |
0,62 |
0,79 |
0,885 |
0,95 |
0,985 |
0,995 |
1 |
3. Найти точечные оценки , , асимметрии,эксцесс.
а) мат. ожидание:
=
=
= 4,95
б) дисперсия:
=
=4,0875
в) стандартное отклонение:
=
=
=2,021756662
г) мода:
=
5
д) медиана:
=
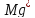=5,5
Центральные моменты:
е) асимметрия:
=
=
=-0,01553279
ж) эксцесс:
=
=
-
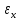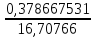3
=-2,97733569
4. Определение параметров распределения, используя метод моментов и наибольшего правдоподобия.
Метод моментов.
Метод моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов рассматриваемого распределения соответствующим эмпирическим моментам того же порядка.
Применяя метод моментов, имеем:
4,95,
т.к. начальный эмпирический момент
первого порядка равен выборочной
средней.
=
=4,0875
т.к. центральный эмпирический момент
второго порядка равен выборочной
дисперсии.
Теперь построим сглаживающую кривую, для этого построим таблицу:
|
X |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
f(x) |
0,029261928 |
0,068056 |
0,123929 |
0,1767 |
0,197264243 |
0,172429351 |
0,118012 |
0,06324 |
0,026534 |
0,008717 |
0,002242 |
Метод наибольшего правдоподобия.
Основу
метода правдоподобия составляет функция
правдоподобия, выражающая плотность
вероятности совместного появления
результатов выборки
В нашем случае она строится на основе
функции плотности вероятности нормально
распределенной случайной величины:
,
где
неизвестными являются параметры
.
Логарифмируем и получаем:
Приравняем к нулю частные производные для нахождения неизвестных оценок, т.е. решим систему правдоподобия:
откуда оценки максимального правдоподобия равны
=
4,95 и
4,0875
Теперь построим сглаживающую кривую, для этого построим таблицу:
|
X |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
f(x) |
0,029261928 |
0,068056 |
0,123929 |
0,1767 |
0,197264243 |
0,172429351 |
0,118012 |
0,06324 |
0,026534 |
0,008717 |
0,002242 |
5. Гипотеза о виде распределения случайных величин.
Данная случайная величина распределена по нормальному закону или закону Гаусса, так как построенная гистограмма отражает характерный вид нормального закона.
ЭТО ОТ 3КУРСА ПРИМЕР РЕШЕНИЯ НЕПРИРЫВНОЙ ВЕЛИЧИНЫ