Математика 2 - 9 вариант[1]

Сибирская государственная автомобильно-дорожная академия

(СибАДИ)

Факультет ЗАОЧНЫЙ

Кафедра ____ЭУТ____

КОНТРОЛЬНАЯ РАБОТА № 2( 9 вариант)

По дисциплине ___ Математика____________________________________

Студента(ки) _____Морозовой Христины Александровна_______________

Курс _______1________________ Шифр ______ ЭУТз-10-34______________

Омск 2011г.

Вариант № 9

Ι. Найти производные данных функций, используя правила вычисления производных.

Перепишем более удобном виде:

Используем правило:

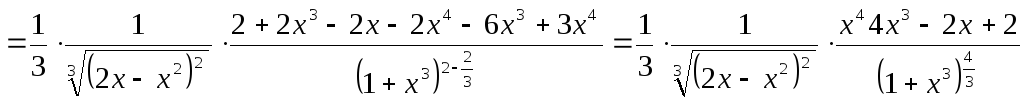
Ответ:

1) Способ:

;

2) Способ:

Ответ:

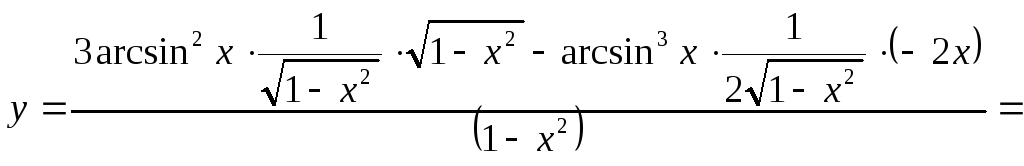
Ответ:

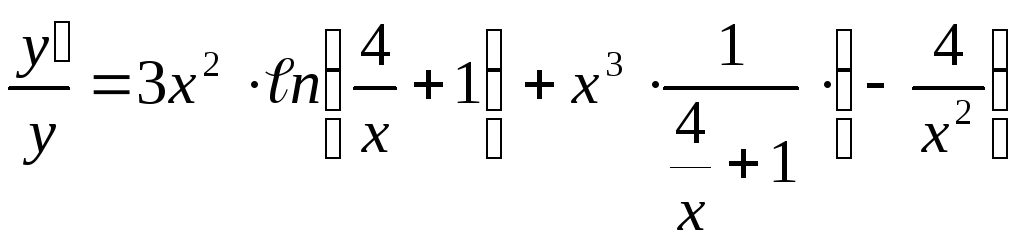
Ответ:

1) Способ:

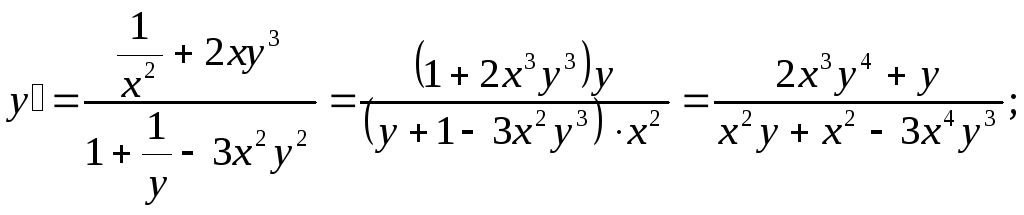
2) Способ:

Ответ:

ΙΙ . Найти для заданной функции

1) Вычисляем

1) Способ:

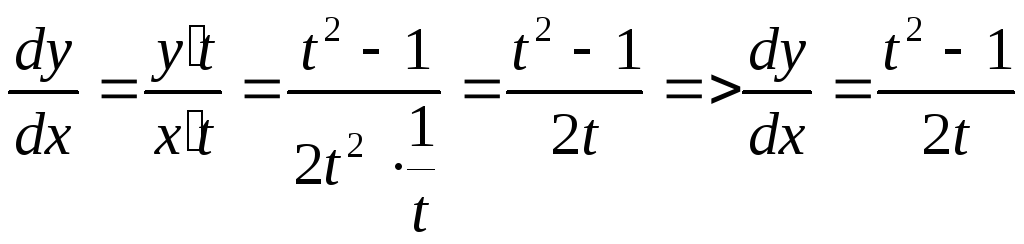
2) Способ:

2) Вычисляем

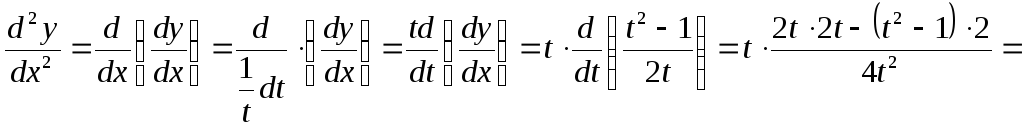
Ответ;

ΙΙΙ ). Исследовать методами дифференциального исчисления функцию и, используя результаты исследования построить график.

1) Область определения

В т.знаменатель функции равен функция не определена

2) График пересекает оси координат в точке

3)

Это функция общего вида

4) Выясним промежутки знакопостоянства.

На промежутке функция принимает отрицательные значения. На промежутке функция положительна.

5) Экстремумы

		0	0; 1	1	1;2	2	2; +
	+	0	-		-	0	+
y		0 max				H min

Промежуток возрастания

Промежуток убывания

Точка- точка максимума

Точка- точка минимума

6) В области определения ΙΙ производная не равна 0, и всюду существует => нет точек перегиба.

при в интервале- выпукл. вниз

при в интервале- выпукл. вверх

7) Ассимптоты

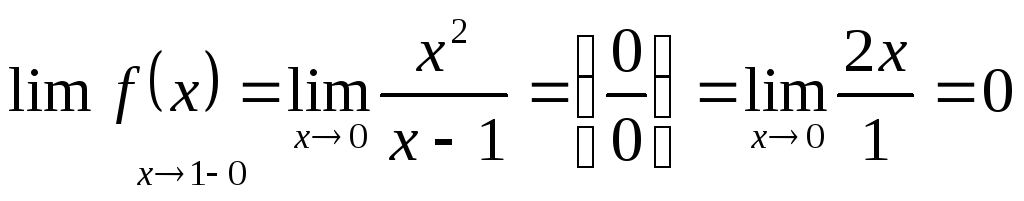
Прямая

Вертикальная Ассимптота.

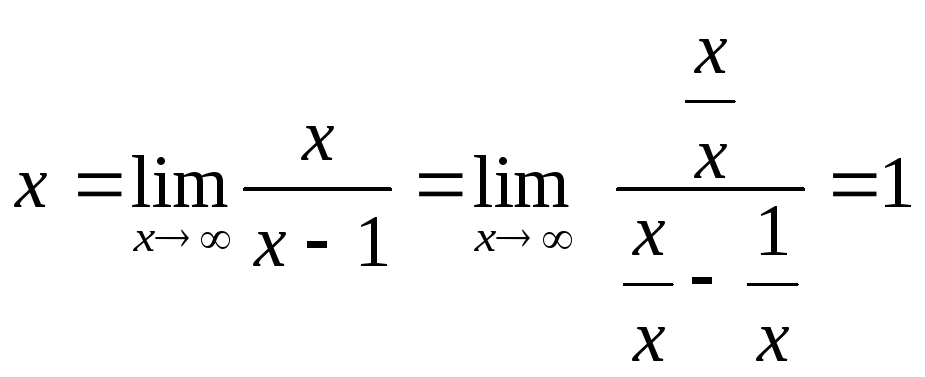
0

наклонная ассимптота

4

1

0 12

IV. Даны функция и две точки:и .

Требуется: 1) вычислить значениев точке ; 2) вычислить приближённое значениефункция в точке , исходя из значенияфункции в точкеи заменив приращение функции при переходе от точки к точкидифференциалом; 3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции её дифференциалом; 4) составить уравнение касательной плоскости к поверхности в точке; 5) линеаризовать данную функцию в окрестности точки .

;

1) Значение функции в точке

2)

3)

4)

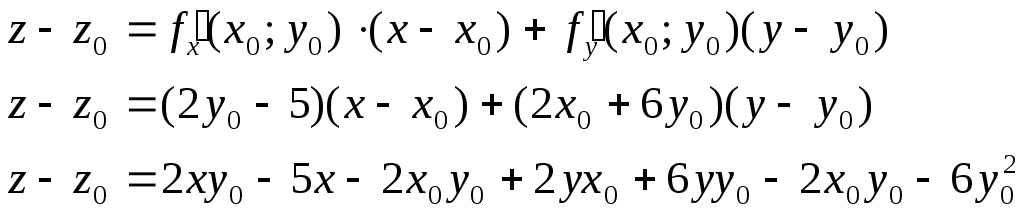
уравнение касательной

плоскости

Ответ; 1)

2)

3)

4) Уравнение касательной плоскости

V. Даны функция точка и вектор . Найти: 1)в точке; 2) производную скалярного поля в точке в направлении вектора.

; ,

1)

Вт.

Вт.

2)

Ответ: 1)

2)

VI. Найти наименьшее и наибольшее значение функции в замкнутой области , заданной системой неравенств. Сделать чертёж.

; ;;

3

-1 0 1

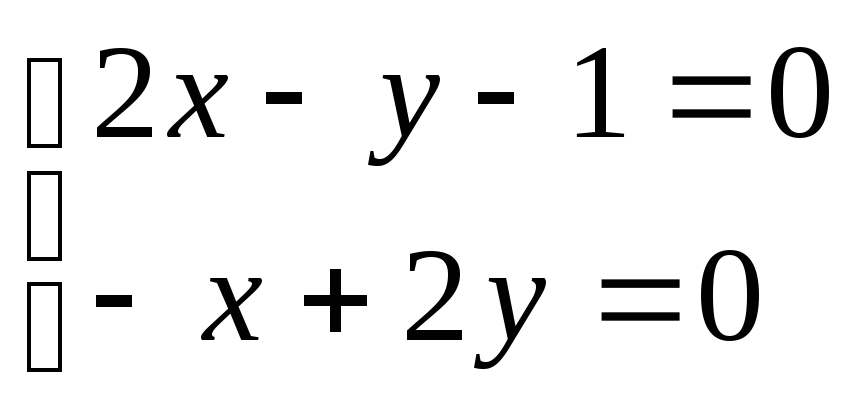
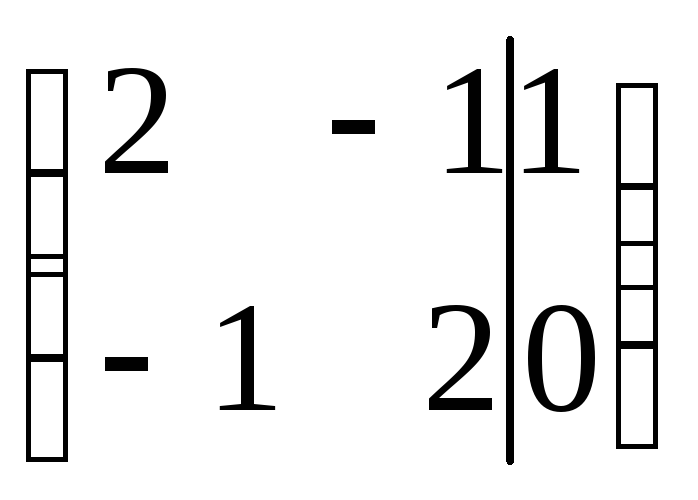
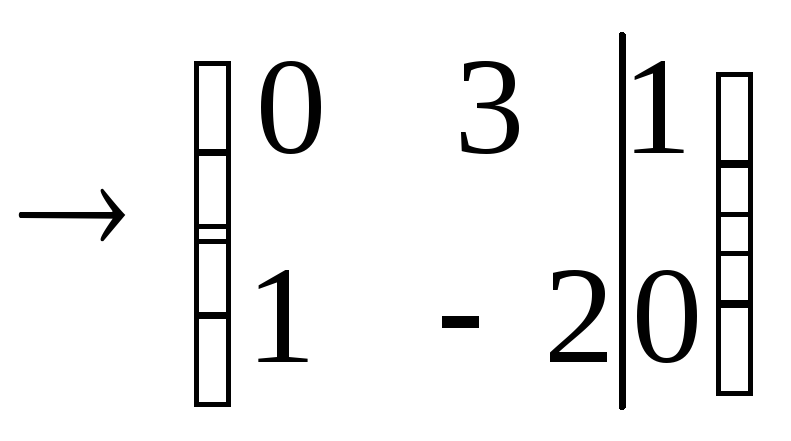
одна стационарная точка

2)

На оси

точка стационарности

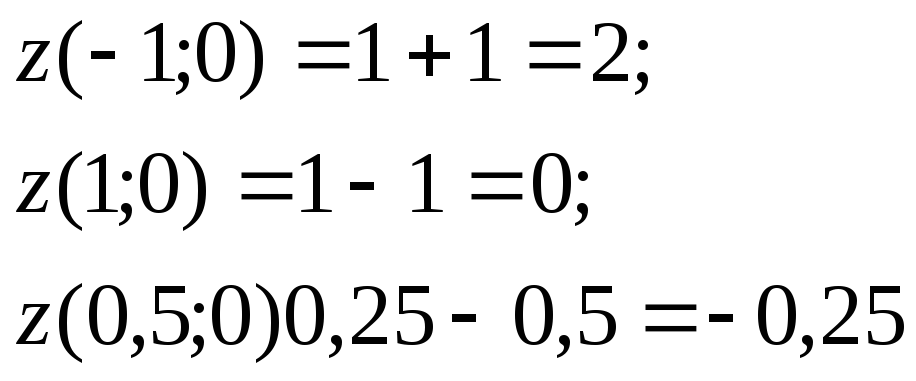
На прямой

- точка стационарности вне области

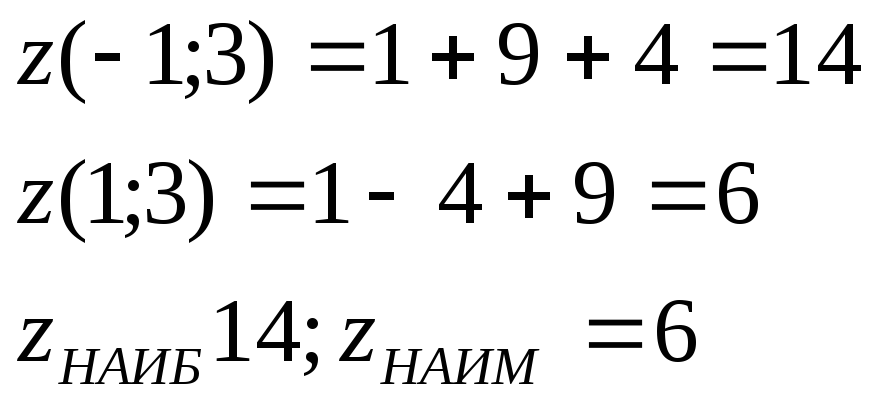
На прямой

не принадлежит области

На прямой

- точка стационарности

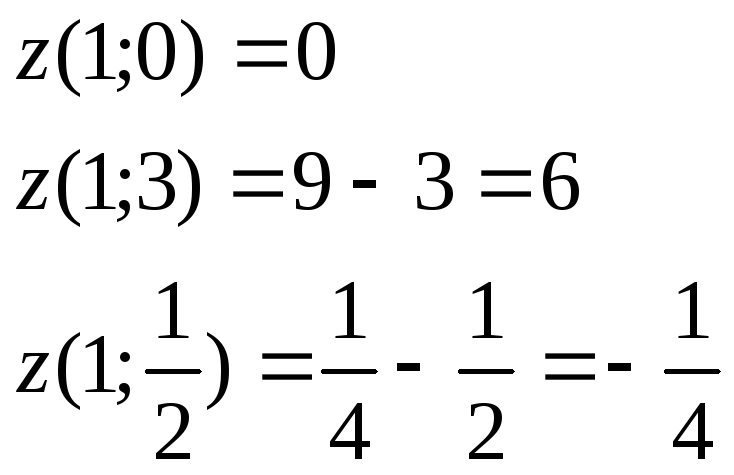
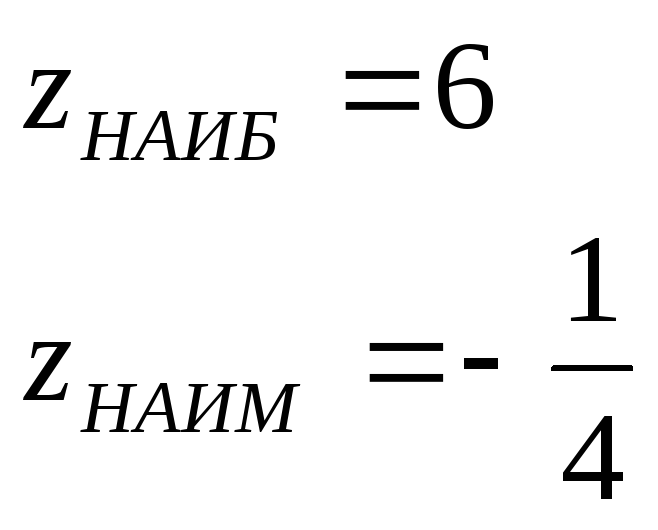
Сравниваем значения на границах и в стационарной точке.

Получаем - на границах

- в стационарной точке

Ответ: в точке

в точке

9