1
.doc
![]() ЗАДАНИЕ
N 1 сообщить
об ошибке
Тема: Основные
понятия, определения, допущения и
принципы
ЗАДАНИЕ
N 1 сообщить
об ошибке
Тема: Основные
понятия, определения, допущения и
принципы
Начало формы




Конец формы
Свойство материала сохранять некоторую часть деформации после снятия нагрузки называется …
|
|
|
|
пластичностью |
|
|
|
|
упругостью |
|
|
|
|
жесткостью |
|
|
|
|
твердостью |
![]()
![]() ЗАДАНИЕ N 2 сообщить
об ошибке
Тема: Внутренние
силы и напряжения
ЗАДАНИЕ N 2 сообщить
об ошибке
Тема: Внутренние
силы и напряжения
Начало формы




Конец формы
Полное напряжение
в точке сечения определяется как
 Предельный
переход позволила осуществить гипотеза …
Предельный
переход позволила осуществить гипотеза …
|
|
|
|
сплошной среды |
|
|
|
|
однородности материала |
|
|
|
|
изотропности материала |
|
|
|
|
начальных размеров |
Решение:
Полное
напряжение в точке сечения
 Предельный
переход позволила осуществить гипотеза
сплошной среды.
Предельный
переход позволила осуществить гипотеза
сплошной среды.
![]()
![]() ЗАДАНИЕ N 3 сообщить
об ошибке
Тема: Перемещение
и деформация
ЗАДАНИЕ N 3 сообщить
об ошибке
Тема: Перемещение
и деформация
Начало формы




Конец формы
Размерность линейной деформации – …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
 L
– первоначальная длина стержня
L
– первоначальная длина стержня
![]() –
длина стержня после приложения к нему
растягивающих сил.
–
длина стержня после приложения к нему
растягивающих сил.
![]() –
абсолютное изменение первоначальной
длины.
–
абсолютное изменение первоначальной
длины.
![]() –
линейная деформация (величина относительная
и безразмерная).
–
линейная деформация (величина относительная
и безразмерная).
![]()
![]() ЗАДАНИЕ
N 4 сообщить
об ошибке
Тема: Модели
прочностной надежности
ЗАДАНИЕ
N 4 сообщить
об ошибке
Тема: Модели
прочностной надежности
Начало формы




Конец формы
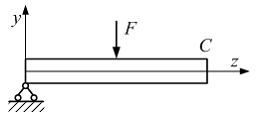 Правый
конец балки (см. рисунок) должен быть
закреплен так, чтобы сечение С
не перемещалось вдоль координатных
осей z
и y
и не поворачивалось в плоскости zy.
Опора, отвечающая таким требованиям,
называется …
Правый
конец балки (см. рисунок) должен быть
закреплен так, чтобы сечение С
не перемещалось вдоль координатных
осей z
и y
и не поворачивалось в плоскости zy.
Опора, отвечающая таким требованиям,
называется …
|
|
|
|
жестким защемлением |
|
|
|
|
шарнирно подвижной |
|
|
|
|
шарнирно неподвижной |
|
|
|
|
скользящим защемлением |
![]()
![]() ЗАДАНИЕ N 5 сообщить
об ошибке
Тема: Продольная
сила. Напряжения и деформации
ЗАДАНИЕ N 5 сообщить
об ошибке
Тема: Продольная
сила. Напряжения и деформации
Начало формы




Конец формы
 На
рисунке показан растянутый стержень.
Между продольными слоями материала …
На
рисунке показан растянутый стержень.
Между продольными слоями материала …
|
|
|
|
отсутствуют нормальные и касательные напряжения |
|
|
|
|
действуют нормальные напряжения |
|
|
|
|
действуют касательные напряжения |
|
|
|
|
действуют нормальные и касательные напряжения |
Решение: В сопротивлении материалов вводится гипотеза о том, что при растяжении-сжатии продольные слои материала в поперечном направлении друг на друга не давят. Согласно этой гипотезе напряжения между слоями материала равны нулю.
![]()
![]() ЗАДАНИЕ N 6 сообщить
об ошибке
Тема: Испытание
конструкционных материалов на растяжение
и сжатие
ЗАДАНИЕ N 6 сообщить
об ошибке
Тема: Испытание
конструкционных материалов на растяжение
и сжатие
Начало формы




Конец формы
Металлический образец, предназначенный для испытаний на сжатие, имеет форму короткого цилиндра, для того чтобы …
|
|
|
|
он не изогнулся в процессе испытаний |
|
|
|
|
он не разрушился |
|
|
|
|
уменьшить влияние сил трения между поверхностями образца и поверхностями плит испытательной машины |
|
|
|
|
он разрушился |
Решение:
 При
сжатии длинного образца возможен его
изгиб. Чтобы исключить это явление
образцы для испытаний на сжатие
изготавливают в форме короткого цилиндра.
При
сжатии длинного образца возможен его
изгиб. Чтобы исключить это явление
образцы для испытаний на сжатие
изготавливают в форме короткого цилиндра.
![]()
![]() ЗАДАНИЕ
N 7 сообщить
об ошибке
Тема: Механические
свойства и механические характеристики
материалов
ЗАДАНИЕ
N 7 сообщить
об ошибке
Тема: Механические
свойства и механические характеристики
материалов
Начало формы




Конец формы
 При
нагружении образца прямоугольного
сечения силами
При
нагружении образца прямоугольного
сечения силами
![]() стрелки
тензометров А и В переместились на 6 и
4 деления соответственно. Базы тензометров
– 20 мм.
Цена деления шкалы тензометров –
0,001 мм.
Модуль упругости материала образца
равен ____ МПа.
стрелки
тензометров А и В переместились на 6 и
4 деления соответственно. Базы тензометров
– 20 мм.
Цена деления шкалы тензометров –
0,001 мм.
Модуль упругости материала образца
равен ____ МПа.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]() ЗАДАНИЕ
N 8 сообщить
об ошибке
Тема: Расчеты
стержней на прочность и жесткость
ЗАДАНИЕ
N 8 сообщить
об ошибке
Тема: Расчеты
стержней на прочность и жесткость
Начало формы




Конец формы
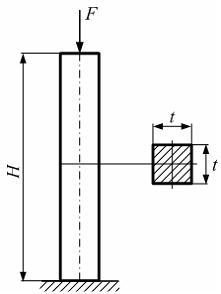 Колонна
находится под действием собственного
веса и силы F,
приложенной в центре тяжести поперечного
сечения (см. рисунок). Известны
величины: F,
H,
t,
Колонна
находится под действием собственного
веса и силы F,
приложенной в центре тяжести поперечного
сечения (см. рисунок). Известны
величины: F,
H,
t,
![]() –
объемный вес материала колонны,
–
объемный вес материала колонны,
![]() –
предел прочности на сжатие. Выражение
для коэффициента запаса прочности имеет
вид …
–
предел прочности на сжатие. Выражение
для коэффициента запаса прочности имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]() ЗАДАНИЕ
N 9 сообщить
об ошибке
Тема: Расчет балок
на прочность
ЗАДАНИЕ
N 9 сообщить
об ошибке
Тема: Расчет балок
на прочность
Начало формы




Конец формы
При расчете балки на прочность по нормальным напряжениям, когда форма и размеры поперечного сечения по длине балки не меняются, опасным считается сечение …
|
|
|
|
в котором действует наибольший изгибающий момент |
|
|
|
|
к которому приложена наибольшая внешняя нагрузка |
|
|
|
|
с наибольшей поперечной силой |
|
|
|
|
расположенное на стыке силовых участков |
![]()
![]() ЗАДАНИЕ N 10 сообщить
об ошибке
Тема: Напряжения
в поперечном сечении стержня при плоском
изгибе
ЗАДАНИЕ N 10 сообщить
об ошибке
Тема: Напряжения
в поперечном сечении стержня при плоском
изгибе
Начало формы




Конец формы
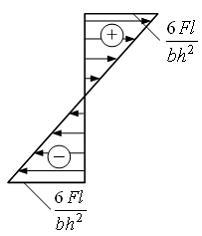
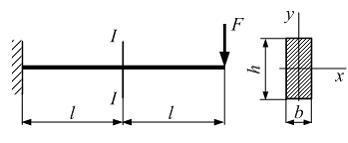 Эпюра
распределения нормальных напряжений
по высоте сечения балки I–I с размерами
b и h
имеет вид …
Эпюра
распределения нормальных напряжений
по высоте сечения балки I–I с размерами
b и h
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Нормальные
напряжения в поперечном сечении балки
распределены по высоте по линейному
закону
 где
где
![]() –
значение изгибающего момента в сечении,
в котором определяется нормальное
напряжение;
–
значение изгибающего момента в сечении,
в котором определяется нормальное
напряжение;
![]() –
осевой момент инерции сечения относительно
главной центральной оси, перпендикулярной
плоскости действия изгибающего момента
в том же сечении; y
– расстояние от главной центральной
оси до точки, в которой определяется
нормальное напряжение.
В сечении I–I
имеем
–
осевой момент инерции сечения относительно
главной центральной оси, перпендикулярной
плоскости действия изгибающего момента
в том же сечении; y
– расстояние от главной центральной
оси до точки, в которой определяется
нормальное напряжение.
В сечении I–I
имеем
 Верхняя
половина сечения I–I работает на
растяжение, нижняя – на сжатие.
Максимальные значения нормальных
напряжений по абсолютной величине
возникают в точках при
Верхняя
половина сечения I–I работает на
растяжение, нижняя – на сжатие.
Максимальные значения нормальных
напряжений по абсолютной величине
возникают в точках при
![]() и
равны
и
равны
 По
полученным значениям
По
полученным значениям
![]() построим
эпюру распределения нормальных напряжений
по высоте сечения I–I.
построим
эпюру распределения нормальных напряжений
по высоте сечения I–I.

![]()
![]() ЗАДАНИЕ
N 11 сообщить
об ошибке
Тема: Поперечная
сила, изгибающий момент и их эпюры
ЗАДАНИЕ
N 11 сообщить
об ошибке
Тема: Поперечная
сила, изгибающий момент и их эпюры
Начало формы




Конец формы
 На
схеме показана отсеченная часть балки
и нагрузка, действующая на нее. Неверным
является утверждение, что изгибающий
момент …
На
схеме показана отсеченная часть балки
и нагрузка, действующая на нее. Неверным
является утверждение, что изгибающий
момент …
|
|
|
|
в сечении В изменяется скачком |
|
|
|
|
в сечении А изменяется скачком |
|
|
|
|
на участке АВ постоянный |
|
|
|
|
на участке ВС переменный |
![]()
![]() ЗАДАНИЕ N 12 сообщить
об ошибке
Тема: Перемещения
при изгибе. Расчет балок на жесткость
ЗАДАНИЕ N 12 сообщить
об ошибке
Тема: Перемещения
при изгибе. Расчет балок на жесткость
Начало формы




Конец формы
 Однопролетная
балка длиной
l, высотой
h нагружена
равномерно распределенной нагрузкой.
Радиус кривизны нейтрального слоя балки
в середине пролета равен
Однопролетная
балка длиной
l, высотой
h нагружена
равномерно распределенной нагрузкой.
Радиус кривизны нейтрального слоя балки
в середине пролета равен
![]() .
Жесткость поперечного
сечения на изгиб
.
Жесткость поперечного
сечения на изгиб
![]() по
всей длине постоянна. Максимальное
нормальное напряжение в балке равно …
(Влияние поперечной силы на изменение
кривизны не учитывать).
по
всей длине постоянна. Максимальное
нормальное напряжение в балке равно …
(Влияние поперечной силы на изменение
кривизны не учитывать).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
При
изгибе балки кривизна нейтрального
слоя связана с изгибающим моментом и
жесткостью поперечного сечения на изгиб
соотношением
 Следовательно,
в середине пролета, в котором возникает
максимальный изгибающий момент, имеем
Следовательно,
в середине пролета, в котором возникает
максимальный изгибающий момент, имеем
 Максимальное
нормальное напряжение найдем по формуле
Максимальное
нормальное напряжение найдем по формуле
 Учитывая,
что
Учитывая,
что
![]() ,
получим
,
получим

![]()
![]() ЗАДАНИЕ N 13 сообщить
об ошибке
Тема: Расчет на
прочность при кручении
ЗАДАНИЕ N 13 сообщить
об ошибке
Тема: Расчет на
прочность при кручении
Начало формы




Конец формы
Стержень круглого поперечного сечения из пластичного материала работает на кручение. При расчете по допускаемым касательным напряжениям за предельное напряжение принимается …
|
|
|
|
предел текучести при чистом сдвиге |
|
|
|
|
предел текучести при растяжении |
|
|
|
|
предел прочности при чистом сдвиге |
|
|
|
|
предел упругости при чистом сдвиге |
Решение: Предел текучести при чистом сдвиге считается предельным напряжением в расчетах по допускаемым напряжениям стержней из пластичного материала, работающих на кручение.
![]()
![]() ЗАДАНИЕ N 14 сообщить
об ошибке
Тема: Чистый сдвиг.
Расчет на сдвиг (срез)
ЗАДАНИЕ N 14 сообщить
об ошибке
Тема: Чистый сдвиг.
Расчет на сдвиг (срез)
Начало формы




Конец формы
 Напряженное
состояние «чистый сдвиг» имеет место
при нагружении тонкостенной трубки по
схеме, показанной на рисунке …
Напряженное
состояние «чистый сдвиг» имеет место
при нагружении тонкостенной трубки по
схеме, показанной на рисунке …
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
4 |
|
|
|
|
3 |