17 Круговые диаграммы в 3-хф. Цепях

Получ. при неоднородных нагр.

Запишем выражение для

При изменении нейтральная точка нагрузки n малое перемещается по полуокружности, диаметр которой является направление

Порядок построения круговой диаграммы:

1. Строим треугольник линейных

напряжений и проводим диаметр AD

2. Из точки А по линии AD откладываем

неизменную проводимость 2g бранном масштабе проводимости mg.

3. Из точки F под проводим линию переменного параметра

4. Из начала точки А опускаем на линию п. п. Из серединыAD восстанавливаем , получаем центр окружности.

Для разметки фаз можно исп. Простую схему, к которой вкл. 2 лампочки и один конденсатор, соед.Звездой

18 Сопоставление схем 3-хф цепей применяемым при питании одноф. Потребителей

При питании одноф. потребителей необходимо обеспечить номинальную величину напр. на зажимах потреб. независимо от вкл. нагрузки. Данному требованию удовл. Схема звезда с нейтральным проводом и схема -ка. Схема звезды без нейтрального провода не может быть исп. в данном случае, т.к. в этой схеме напр. на фазах пропорционально величине сопр. нагрузки.

Сопоставим схему звезда с нейтральным проводом и треугольник при обрыве одной из фаз. При обрыве одной из линий в схеме звезды с нейтральным проводом под нормальным напр. остается 2 группы потреб., тогда как в схеме треуг-ка под нормальным напр. ост. 1 группа. Поэтому надежней явл. Схема звезда с нейтральным пр. В схеме с нейтральным пр. обеспечивается 2 ур. напр. фазное и линейное. Т.о. при питании одноф. потреб. прим. схема звезда с нейтральным пр.

19 Изменение мощности в 3-хф. Цепях

Активная мощность измеряется с помощью ваттметра. В симм. Режиме достаточно одного ваттметра, измеряющего активную мощность фазы

В несимм. режиме при наличии нейтрального провода исп. 3 ваттметра

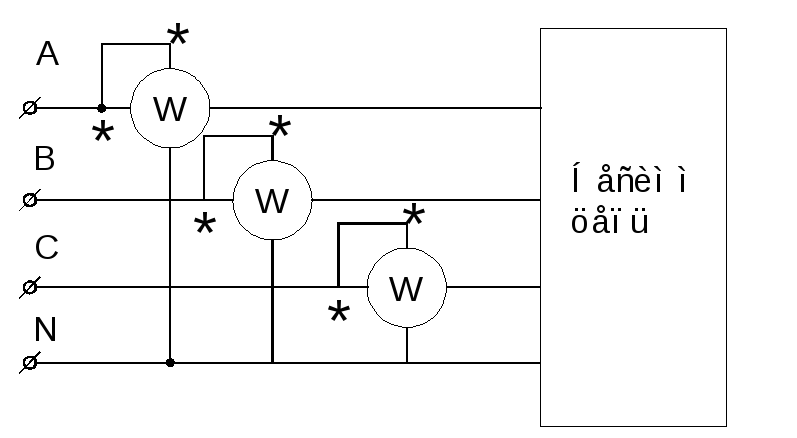
При отсутствии нейтрального провода обычно исп. схема двух ваттметров, вкл.. в любые две фазы. Например:

Покажем, что сумма показаний ваттметра дает активную мощность, потребляемую всей цепью.

Т.о. сумма показаний двух ваттметров дает активную м. всей цепи.

20 Вращающееся магнитное поле

Синусоидальный ток создает пульсир. магн. поле, в к-ой вектор магн. индукции оставаясь неизменным по напр. изм. по величине по синусоидальному закону.

Вектор магн. индукции напр. плоскости витка с током. Возьмем 3 витка, сдвинутые др. относ. др. наи пропустим по этим виткам 3-хф. систему токов.

Вычислим величину суммарного вектора магн. индукции для различных моментов времени

Т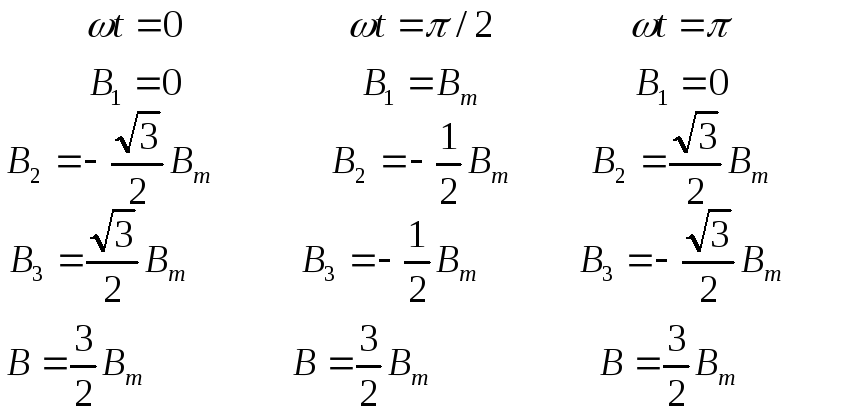.о. симм. система токов создает круговое вращающееся магн. поле, т.е. вектор магн. инд. остается неизменным по величине и вращается с уг. ск-ю равной уг. частоте, т.е. за один период совершает один оборот.

Круговое вращ. магн. поле позволяет осуществить создание асинхронного 3-хф. двигателя.

20 Метод симм. Составляющих

М.с. сост. основан на представлении несимм. 3-хф системы величин в виде суммы 3-х симм. 3-хф. систем.

Расчет проводится отдельно для каждой симм. системы и получ. результаты суммируются

Сущ.3 симм. системы:

1.Симм. система с нулевой последовательностью.

2. Симм. система обратной последовательности

3. Симм. система прямой последовательности

Симм. система прямой последовательности- это 3 вектора одинаковой величины сдвинутые др. относ. др. на 120 град. с прямой последовательностью чередования фазABC.Симм. система обратной последовательности – это 3 вектора сдвинутые др. относ. др. на 120 град. с обратной посл. чередования фаз.Симм. система с нулевой последовательностью- это 3 одинаковых вектора