7. Расчет несимметричного режима в схеме соединенной звездой с нейтральным проводом

Если заданы фазные напр. генератора

, то можно считать их принадлежащими

3-м ист. и представить ген. в симметрич.

схеме

Применим для расчета этой схемы метод

2-х узлов, в соответствии с которым рассчитываем напр. м/у нейтральными точками ген. и нагрузкой , которое наз. смещением нейтрали

, , , …

Затем токи в фазах и ток в нейтральном проводе рассчитываем по закону Ома

, , ,

; , , , , ,

Обрыв нейтрали

, ,

Токи рассчитываются также, а ток в нейтрали будет равен 0

8. Расчет несимметричного режима в схеме звезды без нейтрального провода

При отсутствии нейтрального провода задаются обычно линейные напряжения ген.и их сумма равна0

Поэтому достаточно задать два из них.

И ген. можно представить несимметричной

схемой с двумя ист. ЭДС, включенными в

люб. две фазы, при этом ЭДС ист. равны

соответствующим линейным напряжениям

Представим схему, в которой ЭДС

включены в фазы В и С

,

По методу двух узлов находим смещение нейтрали

, , , ,

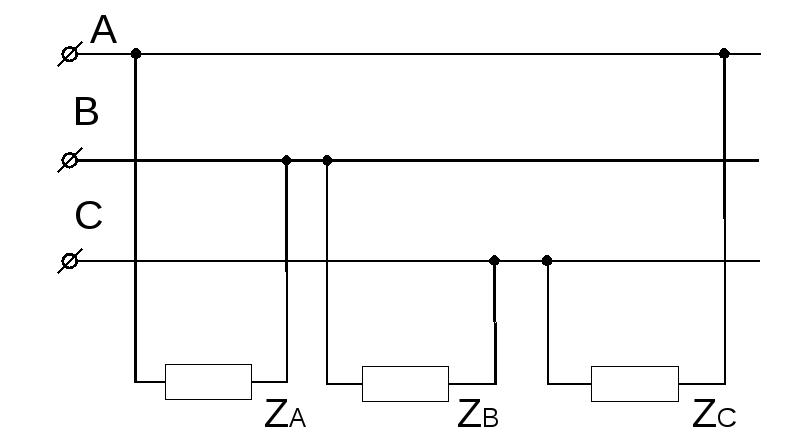
9. Расчет несимметричного режима в схеме треугольника

Для расчета целесообразно заменить треугольник сопротивлений эквивалентной звездой и рассчитать линейные токи по рассмотренной ранее методикой

, , ,

Для расчета фазных токов в исходной схеме треугольника необходимо найти линейное напряжение м/у вершинами треугольника

, , , , ,

, ,

Фазные токи по закону Ома ,…

11. А.Р в схеме звезда с нейтральным проводом:

В симметричном режиме токи образуют симметрич. систему токов и ток в нейтральном проводе равен 0

Обрываем линию, при этом становится равным 0. За счет наличия нейтрального провода смещение нейтрали не возникнет, поэтому напр. на фазах В и С останется неизменным и токи в этих фазах тоже не изменятся. Диаграмма для напр. ост. Такой же как в симметрич. режиме. Построим диаграмму токов.

, , ,

В результате обрыва в фазах В и С токи не изменяются, но возник ток в нейтрале равный по величине фазному току

П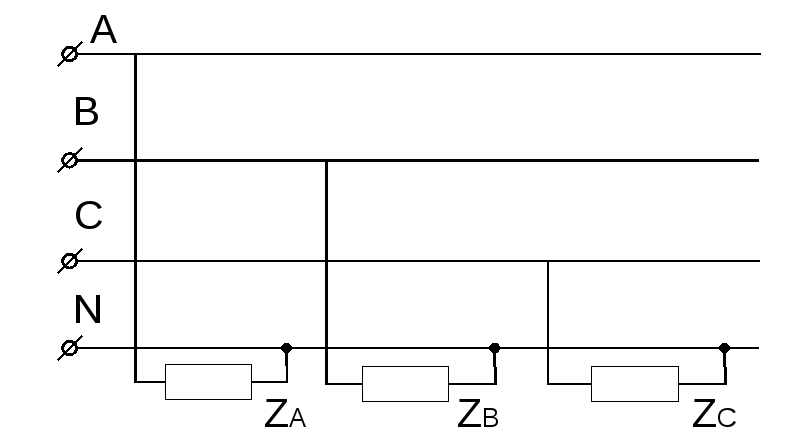ри к. з. одной из фаз нагрузки ток в этой фазе будет ограничиваться только внутренним сопротивлением ген. и может достигнуть недопустимых величин,

12. А.Р в 3-х ф. Цепи соединенной звездой без нейтрального провода

Диаграмма такая же. Обрыв линейного провода, например линии А

При обрыве линии А напр. в фазах В и С изменится и станут равными половине линейного напряжения . На векторной диаграмме нейтральная точка нагрузки лежит на середине лин. напр.

К. з. в одной из фаз нагрузки. При к. з в фазе А потенциал нейтральной точки нагузки n становится равным точки А.

Напр. в фазе В и С становятся равными лин. напр., т.е. увеличивается в раз, соответственно в увелич. токи в этих фазах

При к. з. ток в короткозамкнутой фазе возрастает в 3 раза по сравнению с симметрич. режимом.

16 Линейные диаграммы в трехфазных цепях

Рассмотрим 3-хф. цепь, соединенной звездой без нейтрального провода

Представим ген. эквивалентной схемой с двумя ист. ЭДС, вкл. В фазы В и С

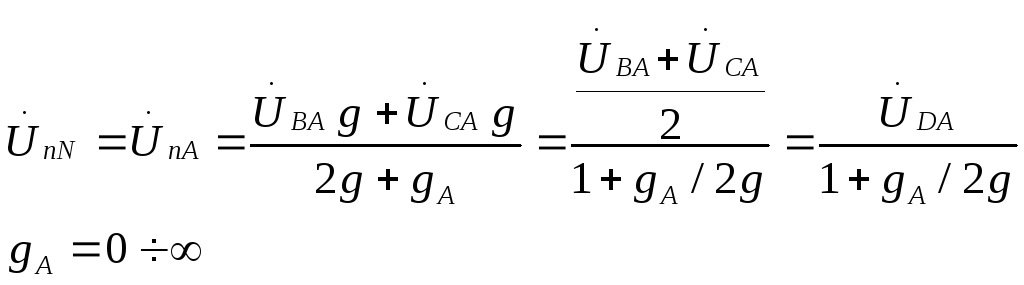
Поделим числитель

и знаменатель 2g

- сим. режим

т.D– х.х..

т.А- к.з.

т.n- сим. режим

вверх по AD

При изм. нейтральная точка нагрузки n малое перемещ. по прямой м/у т.А ит.D, т.е. получаем лин. Диаграмму