4. Свойства определенного интеграла

При введении понятия определенного интеграла предполагается a<b. Обобщим понятие определенного интеграла на случай, когда a=b и a>b.

В этих случаях соответственно полагаем по определению

где f(x) – любая функция;

где f(x) - функция, интегрируемая на отрезке [b,a] (b<a).

Определенный интеграл обладает следующими свойствами:

1. Каковы бы ни были числа а, в, с, всегда имеет равенство

(здесь и в дальнейшем предполагается, что интегралы, входящие в доказываемые формулы, существуют),

2. Постоянный множитель можно выносить за знак определенного интеграла, т. е.

3. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов, т. е.

Эти свойства доказываются путем построения соответствующих интегральных сумм и перехода к пределу при _R0.

Следующие свойства определенного интеграла выражаются с помощью неравенств.

4. Если всюду на отрезке [a, b] функция f(x)  0, то

Доказательство. В самом деле, так как

то переходя к пределу при _R0 получаем

5. Если всюду на отрезке [a, b] функция f(x)  g(x), то

(4.1)

Доказательство.

Так как g(x) – f(x)  0, то

В силу свойства 3

откуда получаем неравенство (4.1).

5. Если функция f(x) интегрируема на [a,b],то функциятакже интегрируема на [a,b] и имеет место

Докажем равенство

, (4.2)

которое понадобится в последующем.

Подынтегральная функция f(x) = 1. Интегральная сумма для неё выразится формулой

Итак, любая интегральная сумма для функции f(x) = 1 равна b – a, поэтому и предел ее равенb–a,т. е. справедливо равенство (4.2).

Теорема 5.Еслиmи М -соответственное наименьшее и наибольшее значения функцииf(x) на отрезке [a,b],a<b, то

(4.3)

Доказательство.По условию для любогоx[a,b] имеемmf(x)M.

По свойствам 5и 2

Учитывая формулу (4.2),получим соотношение (4.3).

Теорема 6 (о среднем). Если функцияf(x) непрерывна на отрезке [a,b], то на этом отрезке существует хотя бы одна точка С такая, что

(4.4)

Доказательство. Так как f(x) непрерывна на [a, b], то существуют числа m и M такие что mf(x)Mдля всех x[a,b].

Отсюда по теореме 5 находим

,

откуда 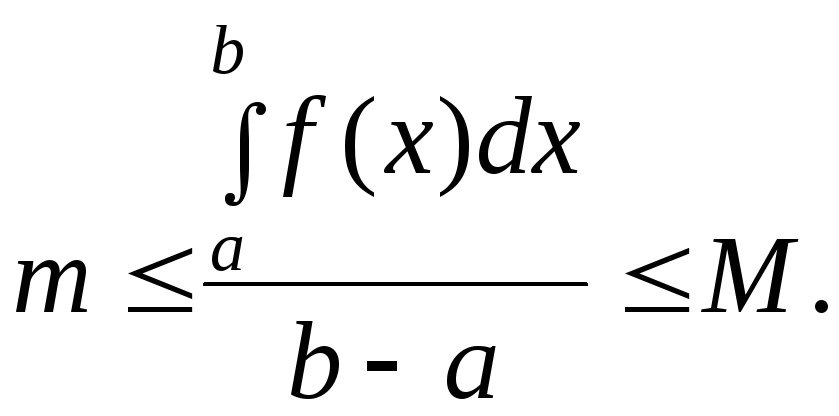Положим (mM).

Так как  заключено между наименьшим и наибольшим значением непрерывной функции f(x) на [a, b] (риc.3), то по теореме о прохождении

Рис. 3

функции через любое промежуточное значение существует точка С[a,b] такая, что f(c ) =  или

а это равносильно равенству (4.4).

Равенство (4.4) называется формулой среднего значения, а число f(C)= носит название среднего значения функции f(x) на отрезке [a, b].

Из формулы (4.4) имеем