Выборка и ее представление

Смоленск 2009

Пусть для изучения количественного (дискретного или непрерывного) признака Х из генеральной совокупности извлечена выборка x₁, x₂ ,...,x_k объема n. Наблюдавшиеся значения x_i признака Х называют вариантами, а последовательность вариант, записанных в возрастающем порядке, – вариационным рядом.

Статистическим распределением выборки называют перечень вариант x_i вариационного ряда и соответствующих им частот n_i (сумма всех частот равна объему выборки n) или относительных частот w_i (сумма всех относительных частот равна единице).

Статистическое распределение выборки можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты интервала принимают сумму частот вариант, попавших в этот интервал).

Эмпирическая функция распределения: Эмпирической функцией распределения (функцией распределения выборки) называют функцию F^*(x), определяющую для каждого значения х относительную частоту события Х<х:

F^*(x)=n_x/n,

где n – число вариант, меньших x; n – объем выборки.

Эмпирическая функция обладает следующими свойствами:

1) Значения эмпирической функции принадлежат отрезку [0;1];

2) F^*(x) – неубывающая функция;

3) Если x₁ –наименьшая варианта, а x_k – наибольшая, то F^*(x)=0 при x≤x₁ и F^*(x)=1 при x>x_k.

Дискретное распределение признака Х. Полигоном частот называют ломаную, отрезки которой соединяют точки (x₁, n₁), (x₂ , n₂),..., (x_k , n_k), где x_i – варианты выборки и n_i – соответствующие им частоты.

Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x₁; w₁), (x₂; w₂), ..., (x_k; w_k), где x_i – варианты выборки и w_k – соответствующие им относительные частоты.

Непрерывное распределение признака Х. При непрерывном распределении признака весь интервал, в котором заключены все наблюдаемые значения признака, разбивают на ряд частичных интервалов длины h и находят n_i – сумму частот вариант, попавших в i-й интервал. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению n_i/h (плотность частоты). Площадь частичного i-го прямоугольника равна h(n_i/h)=n_i – сумме частот вариант, попавших в i-й интервал. Площадь гистограммы частот равна сумме всех частот, т.е. объему выборки n.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению w_i/h (плотность относительной частоты). Площадь частичного i-го прямоугольника равна h(w_i/h)=w_i – относительной частоте вариант, попавших в i-й интервал. Площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.

Цель занятий: 1. Научить студентов правильно представлять статистический материал и проводить первоначальную его обработку.

2. Закрепить в сознании студентов соответствие между понятиями прикладной и математической статистики:

В прикладной статистике	В математической статистике
Генеральная совокупность Выборка	Х –случайная величина x1, x2 ,..., xn – результаты наблюдений Х

К занятию по данной теме должны быть подготовлены следующие вопросы.

1. Почему важно исследование распределения генеральной совокупности по количественным признакам?

2. Какие основные задачи математической статистики?

3. Что понимают под выборочным методом?

4. Что понимают под теоретической выборкой? Чем являются выборочные характеристики, если выборка теоретическая?

Задача 1. В супермаркете проводились наблюдения над числом Х покупателей, обратившихся в кассу за один час. Наблюдения в течение 30 часов (15 дней в период с 9 до 10 и с 10 до 11 часов) дали следующие результаты:

70, 75, 100, 120, 75, 60, 100, 120, 70, 60, 65, 100, 65, 100, 70, 75, 60, 100, 100, 120, 70, 75, 70, 120, 65, 70, 75, 70, 100, 100.

Число Х является дискретной случайной величиной, а полученные данные представляют собой выборку из n=30 наблюдений. Требуется составить ряд распределения частот (вариационный ряд).

Решение. Вначале составим ранжированный ряд:

60, 60, 60, 65, 65, 65, 70, 70, 70, 70, 70, 70, 70, 75, 75, 75, 75, 75, 100, 100, 100, 100, 100, 100, 100, 100, 120, 120, 120, 120.

Получено шесть групп, т.е. шесть различных значений случайной величины (шесть вариант). Для каждой группы подсчитаем частоту значений варианты и соответствующую относительную частоту. Все результаты укажем в табл. 1, которая и будет представлять вариационный ряд.

Таблица 1

Номер группы	i	1	2	3	4	5	6
Число обращений покупателей в кассу	xi	60	65	70	75	100	120
Частота	mi	3	3	7	5	8	4
Относительная частота	pi	3/30	3/30	7/30	5/30	8/30	4/30

Задача 2. В таблице 2 приведена выборка результатов измерения роста 105 студентов (юношей). Измерения проводились с точностью до 1 см.

Таблица 2

155	170	185	180	188	152	173	178	178	168	185
173	170	183	175	173	170	183	175	180	175	193
178	183	180	197	178	181	187	168	174	179	184
183	178	180	178	163	166	178	175	182	190	167
170	178	183	170	178	181	173	168	185	175	170
155	169	186	179	189	155	174	179	179	169	186
174	171	184	175	193	178	184	180	196	175	181
188	168	179	178	183	184	178	181	177	163	166
178	175	183	190	167	170	178	183	170	178	182
173	168	186	176	171	188

Требуется составить интервальный вариационный ряд.

Решение. Очевидно, что рост юношей есть случайная непрерывная величина. Найдем сначала минимальное и максимальное значения случайной величины: x_min=152 см, x_max=196 см. Тогда интервал варьирования R («размах») будет равен R=x_max-x_min= =44 см.

На практике обычно считают, что правильно составленный ряд распределения содержит от 6 до 15 частичных интервалов, однако фактическое число частичных интервалов и, соответственно, размер интервала определяются условиями конкретной задачи.

В нашем случае удобно выбрать длину частичного интервала равной 5 см, тогда число частичных интервалов, начиная со 150 см и кончая 200 см, будет равно 10. Соответствующий интервальный вариационный ряд приведен в таблице 3.

Таблица 3

Индекс интервала i	Рост студентов (интервалы) xi<X≤xi+1	Частота mi	Относительная частота p*i
1	150-155	4	0,0381
2	155-160	–	–
3	160-165	2	0,0190
4	165-170	19	0,1810
5	170-175	19	0,1810
6	175-180	26	0,2476
7	180-185	21	0,2000
8	185-190	10	0,0953
9	190-195	2	0,0190
10	195-200	2	0,0190

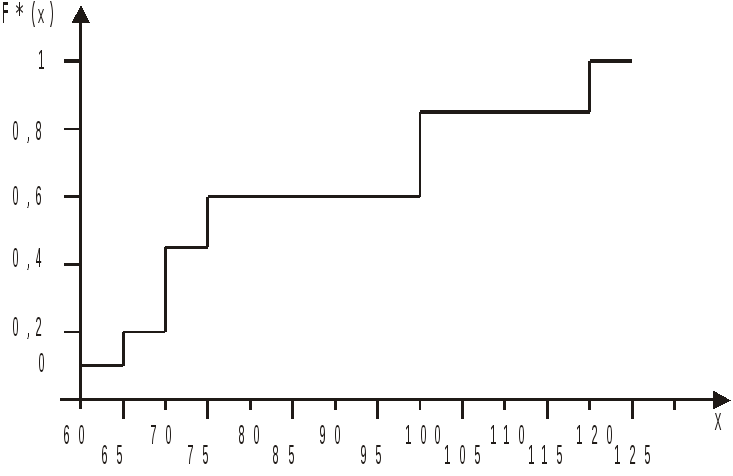
Задача 3. Построим выборочную функцию распределения по данным табл. 1.

Объем выборки по условию примера n=30. Наименьшая варианта равна 60, значит, n_x=0 при x≤60. Тогда F^*(x)=0/30=0 при х≤60. Если 60<x≤70, то неравенство X<x выполняется для вариант x₁=60 и x₂=65, а эти варианты встречаются по 3 раза, поэтому n_x=6 и F^*(x)=6/30 и т.д. Результат вычисления F^*(x) для всего множества значений вариант дискретной случайной величины приведен в таблице.

x	F*(x)
x≤60	0
60<x≤65	p*1 = 3/30
65<x≤70	p*1+ p*2 = 6/30
70<x≤75	p*1 +p*2 +p*3 = 13/30
75<x≤100	p*1 +p*2 +p*3 +p*4 = 18/30
100<x≤120	p*1 +p*2 +p*3 +p*4 +p*5 = 26/30
x>120	p*1 +p*2 +p*3 +p*4 +p*5 +p*6 = 30/30 = 1

График функции приведен на рис. 1.

В данном примере функция F^*(x) есть выборочная функция распределения дискретной случайной величины и построена она по дискретному вариационному ряду.

Задача 4. Построим выборочную (эмпирическую) функцию распределения по данным табл. 2. Очевидно, что для функцияF^*(x)=0, так как n_x=0.

Используя результаты рассчетов, представленные в табл. 3, подсчитаем на концах интервалов значения функции F^*(x) в виде «нарастающей относительной частоты».

Индекс интервала i	F*(x)
1	0,0381
2	0,0381
3	0,0571
4	0,2381
5	0,4197
6	0,6667
7	0,8667
8	0,9620
9	0,9810
10	1,0000

Очевидно, что табличные значения не полностью определяют выборочную функцию распределения непрерывной случайной величины, поэтому при графическом изображении такой функции ее доопределяют, соединив точки графика, соответствующие концам интервала, отрезками прямой.

Задача 5. Выборка дана в виде распределения частот:

xi	2	5	7	8	11	13
ni	10	9	21	25	30	5

Найти распределение относительных частот и построить полигон относительных частот.

Решение. Оценим объем выборки: . Тогда вариационный ряд можно записать в виде

xi	2	5	7	8	11	13
	0,10	0,09	0,21	0,25	0,30	0,05

На рисунке приведен полигон относительных частот.

Задача 6. Выборка задана интервальным вариационным рядом

i	xi≤X≤xi+1	mi
1	1–5	10
2	5–9	20
3	9–13	50
4	13–17	12
5	17–21	8

Построить гистограмму выборочной оценки плотности вероятности.

Решение. Длина каждого интервала равна h=4. Объем выборки n=100. Подсчитаем значения m_i/(hn):

xi≤X≤xi+1	1–5	5–9	9–13	13–17	17–21
mi/(hn)	25·10-3	50·10-3	125·10-3	30·10-3	20·10-3

На рисунке представлена гистограмма данного распределения.

Дополнительные задачи.

Таблица 1

i	Выработка в отчетном году в процентах к предыдущему х	Частота (количест-во рабочих) ni	Частость (доля рабочих)	Накоп-ленная частота	Накопленная частость
1	94-100	3	0,03	3	0,03
2	100-106	7	0,07	10	0,10
3	106-112	11	0,11	21	0,21
4	112-118	20	0,20	41	0,41
5	118-124	28	0,28	69	0,69
6	124-130	19	0,19	88	0,88
7	130-136	10	0,10	98	0,98
8	136-142	2	0,02	100	1,00
	∑	100	1,00	–	–

Задача 1. Построить полигон (гистограмму) и эмпирическую функцию распределения рабочих по выработке по данным таблицы 1.

Решение. На рис. 1 изображены полигон (гистограмма) и эмпирическая функция распределения интервального вариационного ряда.

Для интервального вариационного ряда имеем лишь значения функции распределения F_n(x) на концах интервала (см. последнюю графу таблицы). Поэтому для графического изображения этой функции целесообразно ее доопределить, соединив точки графика, соответствующие концам интервалов, отрезками прямой.

Задача 2. Найти среднюю выработку рабочих по данным таблицы 1.

Решение. По формуле для интервального вариационного ряда

,

где числа 97, 103,..., 133, 139 – середины соответствующих интервалов.

Задача 3. Найти медиану распределения рабочих по тарифному разряду по данным таблицы.

Тарифный разряд xi	1	2	3	4	5	6	∑
Частота (количество рабочих) ni	2	3	6	8	22	9	50

Решение. n=50 – четное, следовательно, серединных вариантов два: х₂₅=5 и х₂₆=5. Поэтому =(х₂₅+х₂₆)/2=(5+5)/2=5(%).

Задача 4. Найти медиану распределения рабочих по выработке по данным таблицы 1.

Решение. На рис. 2 проведем горизонтальную прямую y=0,5 (или y=50), соответствующую накопленной частости (или накопленной частоте), до пересечения с графиком эмпирической функции распределения (или кумулятой). Абсцисса точки пересечения и будет медианой вариационного ряда:.

Задача 5. Вычислить дисперсию, среднее квадратическое отклонение и коэффициент вариации распределения рабочих по данным таблицы 1.

Решение. В примере 2 было получено . По определению дисперсия

.

Среднее квадратическое отклонение ; коэффициент вариацииv=(9,35/119,2)100=7,8(%).

Следует отметить, что вычисление дисперсии (особенно в случае, когда отклонения от средней выражаются нецелыми числами) бывает удобнее проводить по формуле. Например, в данном примере вначале найдем

.

Следовательно,

s²=14296,12-119,2²=87,48.

Домашнее задание.

Задача 1. Наблюдается число выигрышей в мгновенной лотерее. В результате наблюдения получены следующие значения выигрышей (тыс. рую.):

0, 1, 0, 0, 5, 0, 10, 0, 1, 0, 0, 1, 5, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 5, 0, 5, 0, 0, 1, 1, 1, 5, 10, 0, 1, 1, 0, 5, 0, 0, 0, 0, 1, 0, 1, 0, 5, 0, 0, 0, 0, 1, 0.

Составить вариационный ряд случайной величины Х – выигрыша в случайной лотерее.

Задача 2. В городе А для определения сроков гарантийного обслуживания проведено исследование величины среднего пробега автомобилей, находящихся в эксплуатации в течение двух лет с момента продажи автомобиля магазином. Получен слудующий результат (тыс. км):

3,0; 25,0; 18,6; 12,1; 10,6; 18,0; 17,3; 29,1; 20,0; 18,3; 21,5; 26,7; 12,2; 14,4; 7,3; 9,1; 2,9; 5,4; 40,1; 16,8; 11,2; 9,9; 25,3; 4,2; 29,6.

Сравнить интервальный вариационный ряд.

Задача 3. На фирме работает 39 человек. Проведено исследование числа рабочих дней, пропущенных каждым работником фирмы в течение месяца. Результаты этого исследования таковы:

0, 1, 3, 0, 2, 3, 5, 7, 3, 5, 2, 10, 7, 5, 0, 2, 5, 10, 5, 3, 1, 9, 15, 10, 1, 0, 2, 3, 5, 7, 7, 6, 5, 3, 0, 7, 10, 13, 0.

Составить интервальный вариационный ряд. Построить функцию распределения случайной величины числа пропущенных рабочих дней.

Задача 4. Построить полигон относительных частот по данным вариационным рядам (n=110):

xi	1	4	5	7	9
mi	10	25	45	20	10

Задача 5. Построить гистограмму относительных частот по данным распределения выборки объема n=100:

i	xi<X≤xi+1	mi
1	3–5	20
2	5–7	25
3	7–9	15
4	9–11	13
5	11–13	12
6	13–15	8
7	15–17	7

СМОЛЕНСКИЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ

Г. С. ЕВДОКИМОВА

ПРАКТИКУМ

ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

И МАТЕМАТИЧЕСКОЙ

СТАТИСТИКЕ

МОДУЛЬ 8