
Вопросы студ матан
.doc-
Величина
 называется функцией переменной величины
называется функцией переменной величины
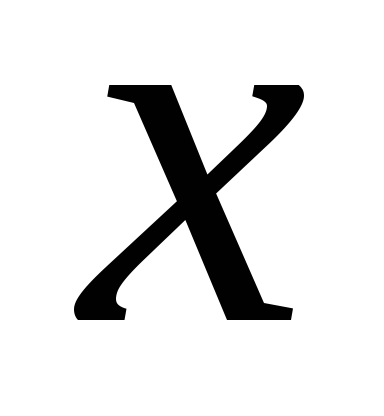 ,
если каждому из тех значений, которые
может принимать
,
если каждому из тех значений, которые
может принимать
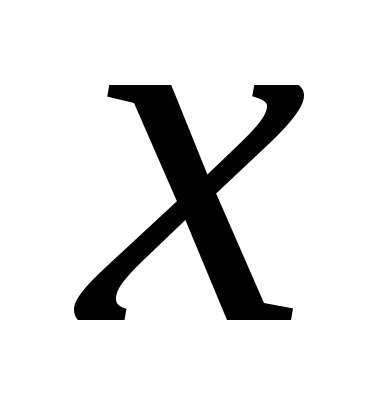 ,
соответствует:
,
соответствует:
-
Функция называется однозначной, если:
-
Функция называется многозначной если:
-
Совокупность всех значений, которые может принимать аргумент
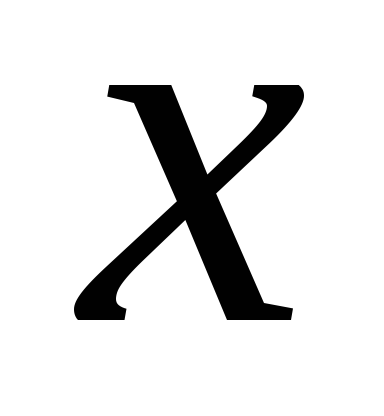 функции
функции
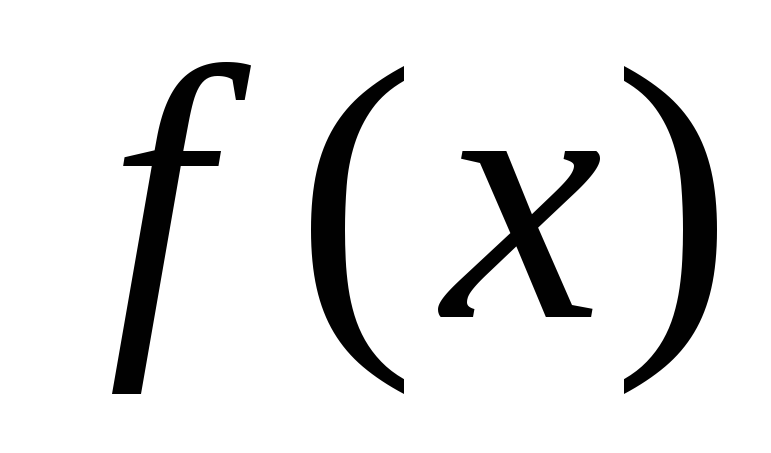 ,
называется:
,
называется: -
Совокупность чисел
 ,
заключенных между числами
,
заключенных между числами
 и
и
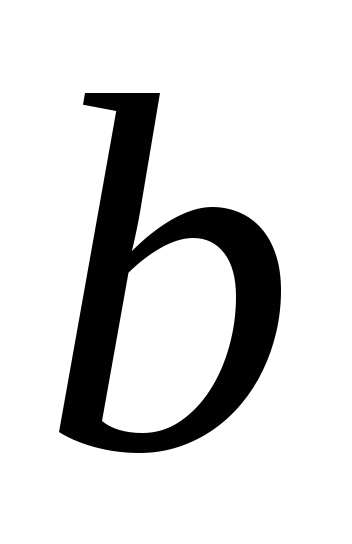 называется:
называется: -
Совокупность чисел
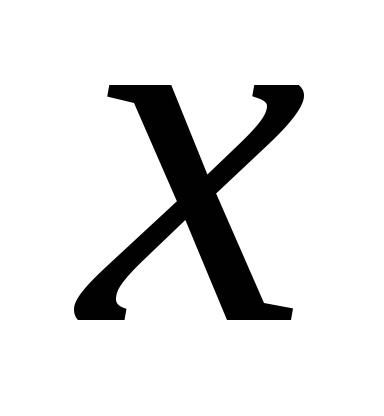 ,
заключенных между числами
,
заключенных между числами
 и
и
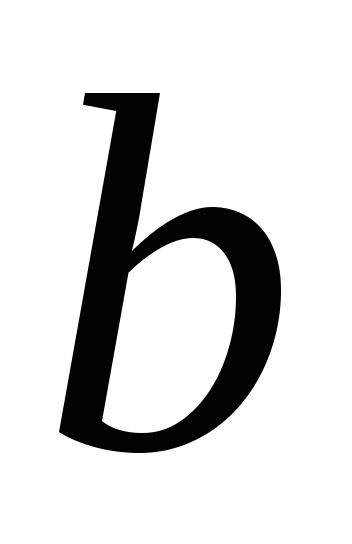 ,
включая сами числа
,
включая сами числа
 и
и
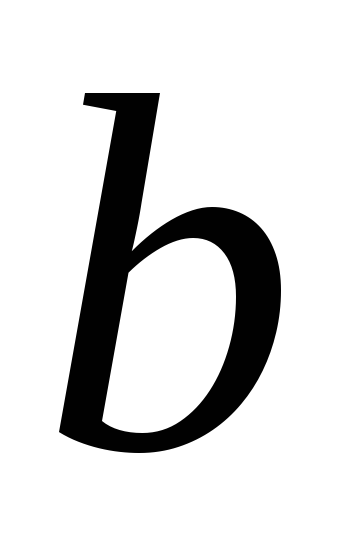 ,
называется:
,
называется: -
Функции подразделяются на:
-
Функция
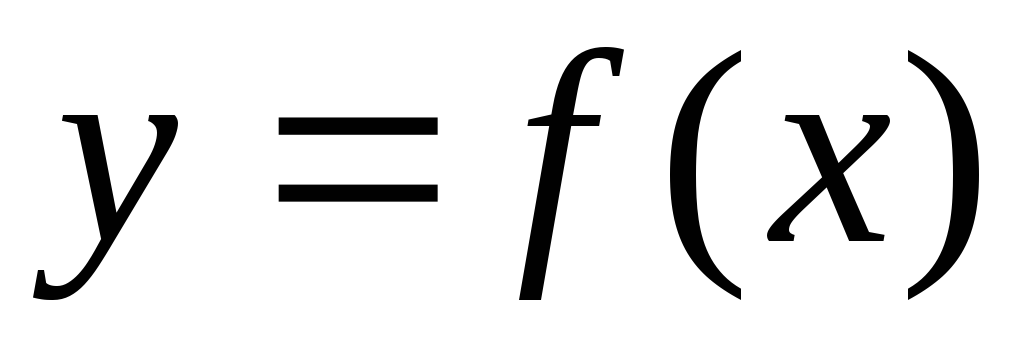 ,
определенная на множестве
,
определенная на множестве
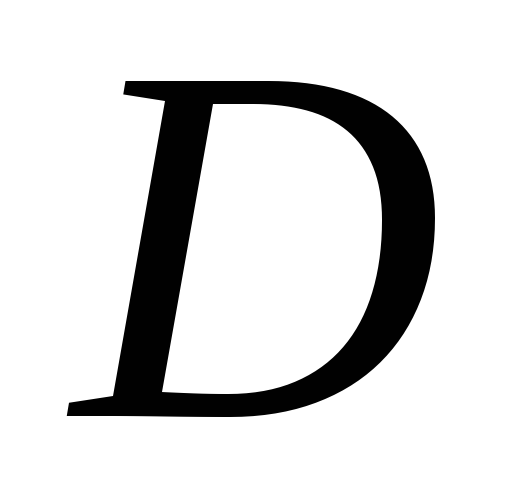 называется четной, нечетной, общего
вида, если:
называется четной, нечетной, общего
вида, если: -
Функция
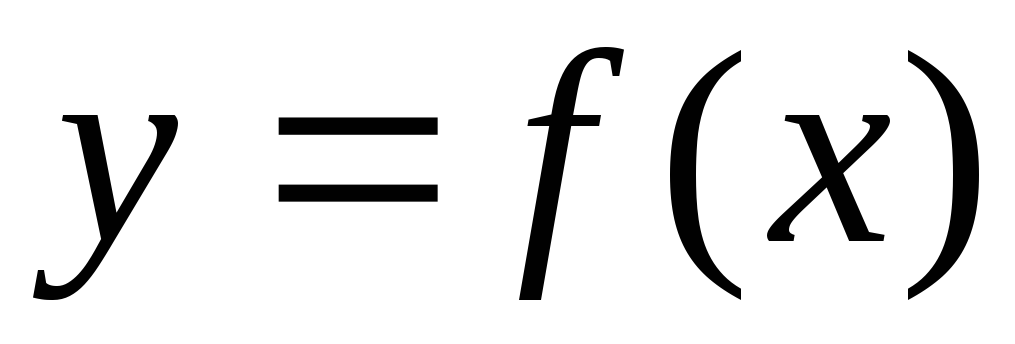 определена на множестве
определена на множестве
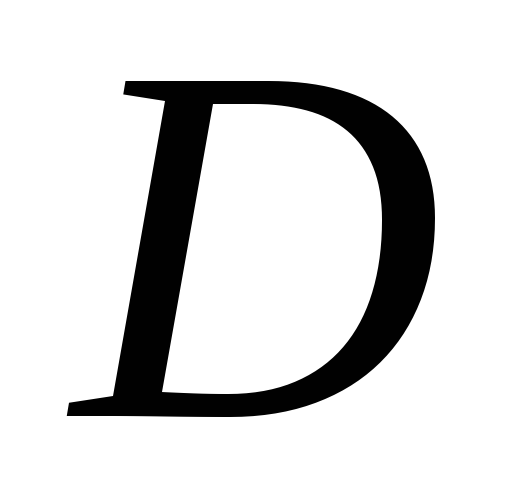 и
и
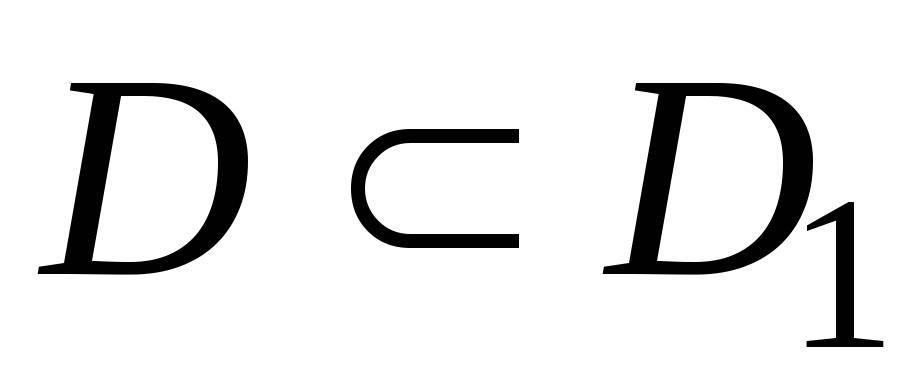 .
Если для любых значений
.
Если для любых значений
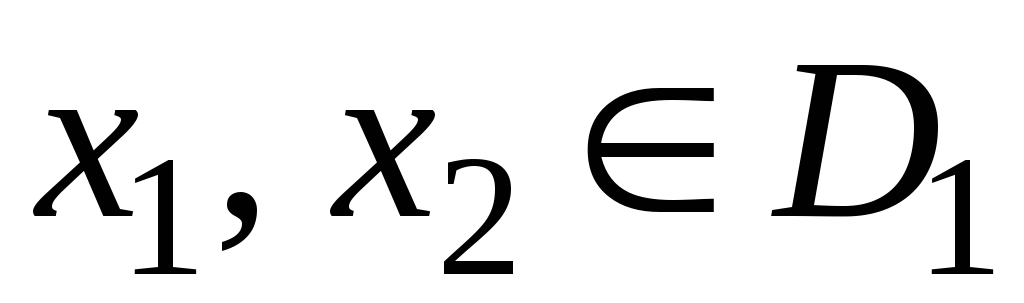 из неравенства
из неравенства
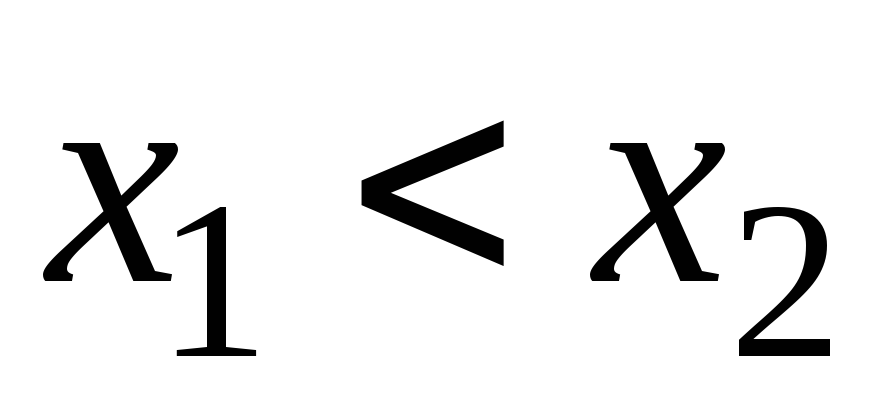 вытекает неравенство
вытекает неравенство
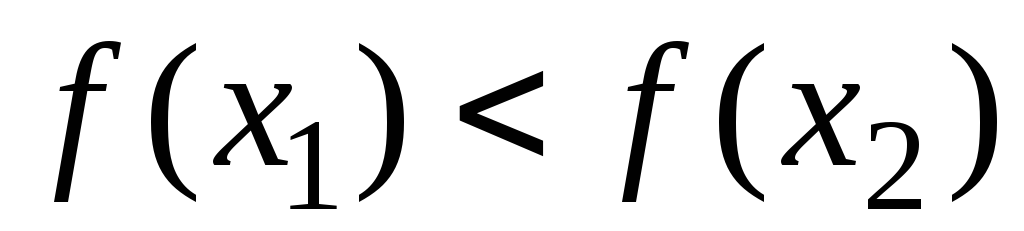 ,
то функция называется:
,
то функция называется: -
Функция
 определена на множестве
определена на множестве
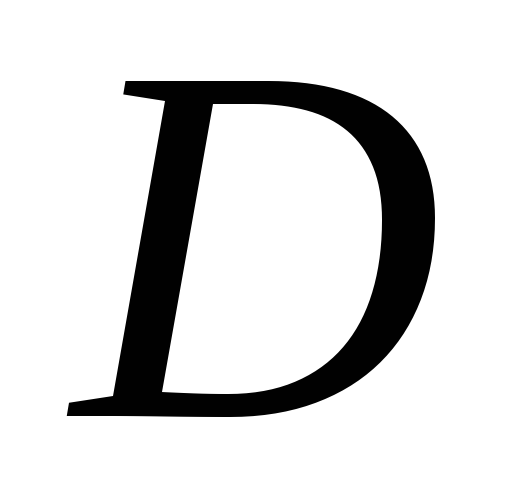 и
и
 .
Если для любых значений
.
Если для любых значений
 из неравенства
из неравенства
 вытекает неравенство
вытекает неравенство
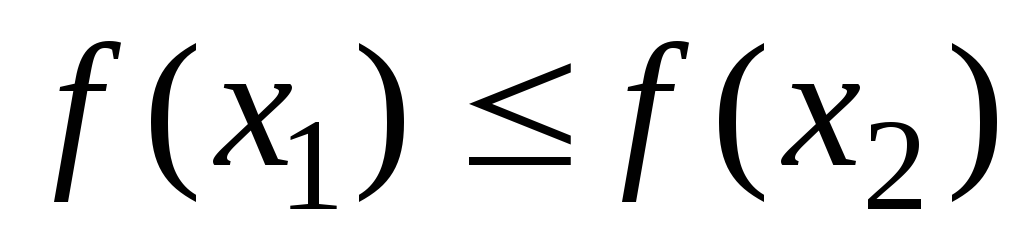 ,
то функция называется:
,
то функция называется: -
Функция
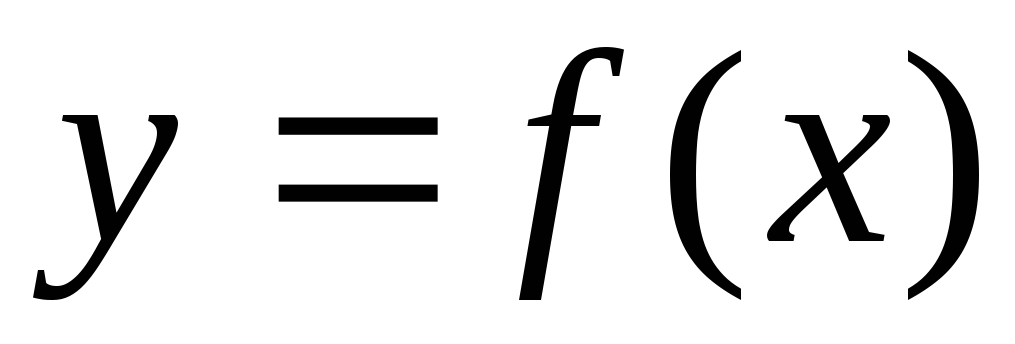 определена на множестве
определена на множестве
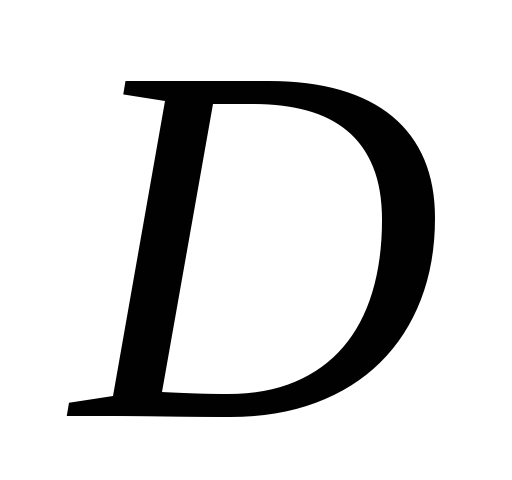 и
и
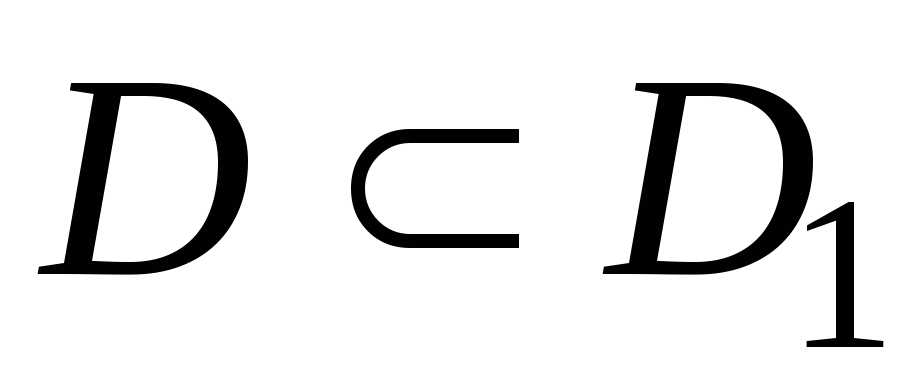 .
Если для любых значений
.
Если для любых значений
 из неравенства
из неравенства
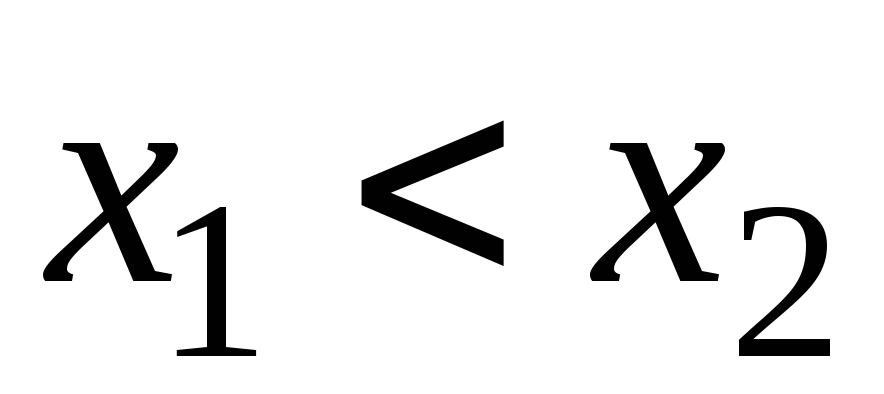 вытекает неравенство
вытекает неравенство
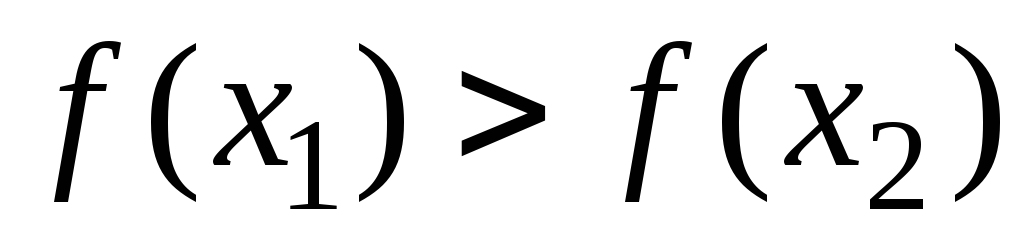 ,
то функция называется:
,
то функция называется: -
Функция
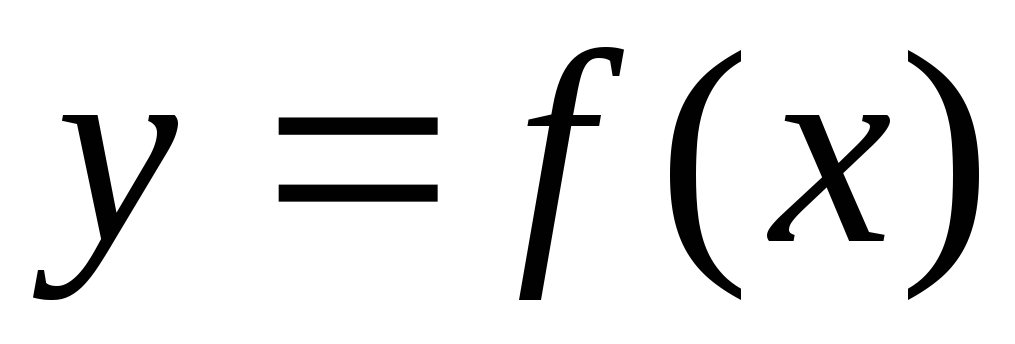 определена на множестве
определена на множестве
 и
и
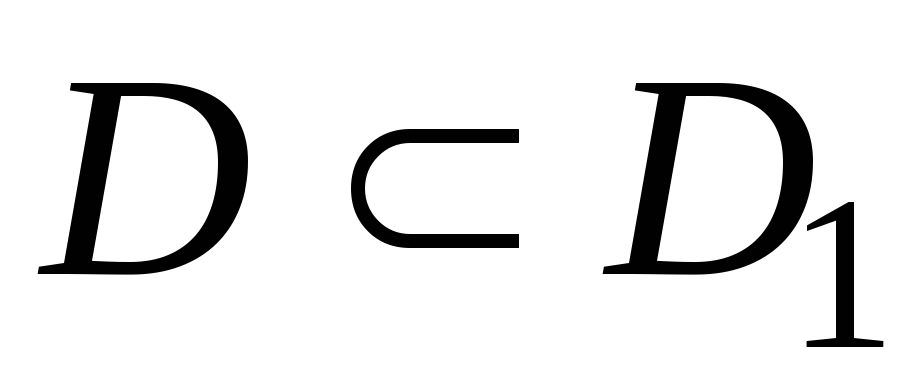 .
Если для любых значений
.
Если для любых значений
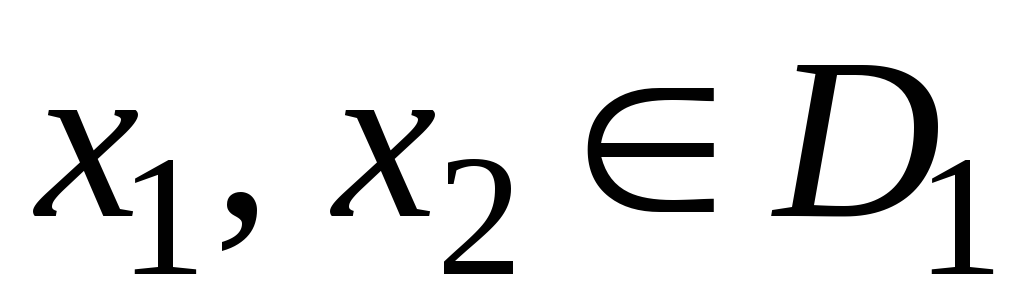 из неравенства
из неравенства
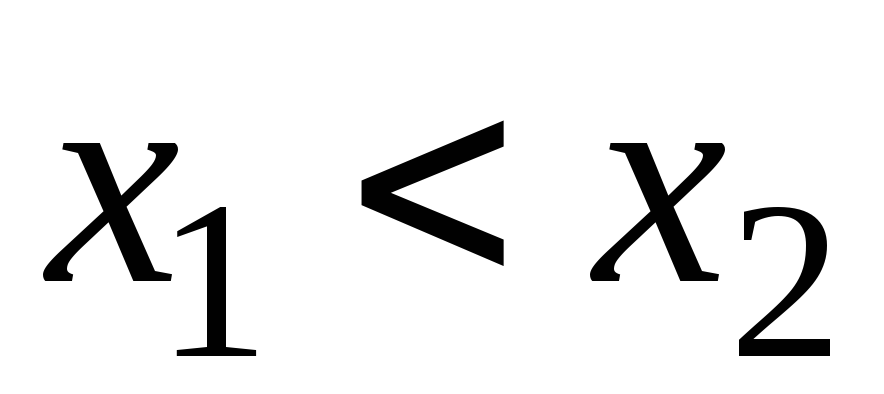 вытекает неравенство
вытекает неравенство
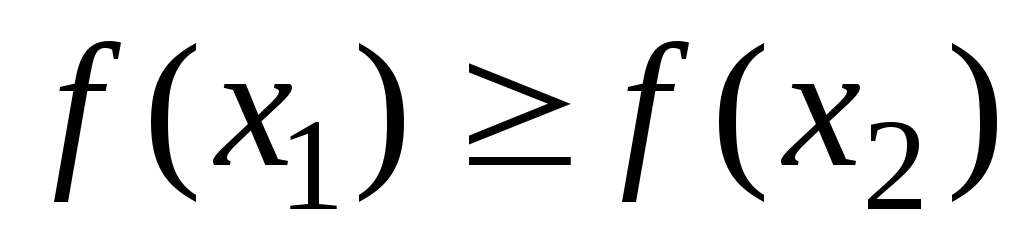 ,
то функция называется:
,
то функция называется: -
Функцию
 ,
определенную на множестве
,
определенную на множестве
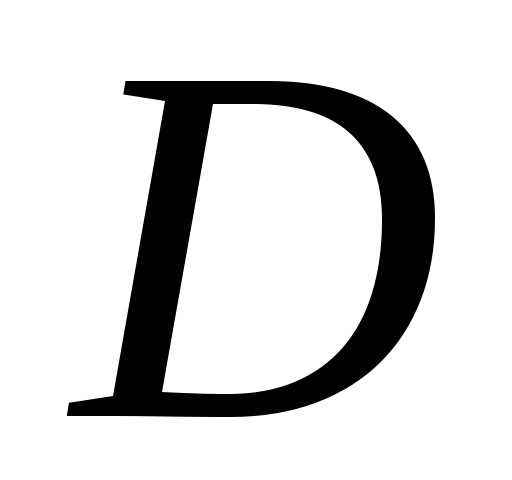 называют __?____ , если существует такое
число
называют __?____ , если существует такое
число
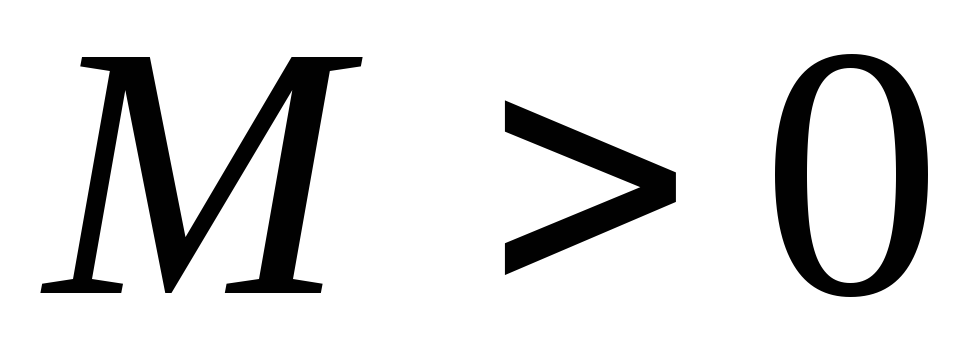 ,
что для всех
,
что для всех
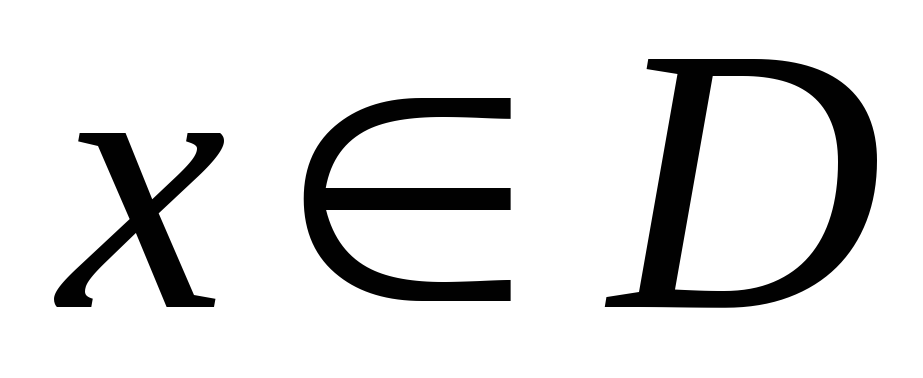 выполняется неравенство
выполняется неравенство
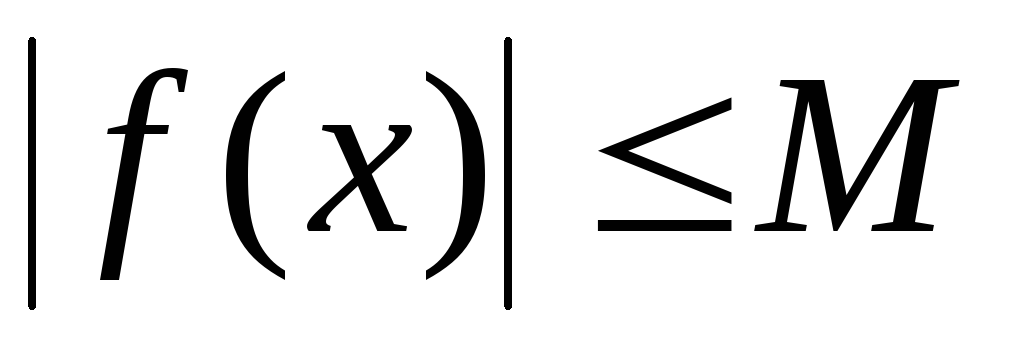 .
. -
Функция
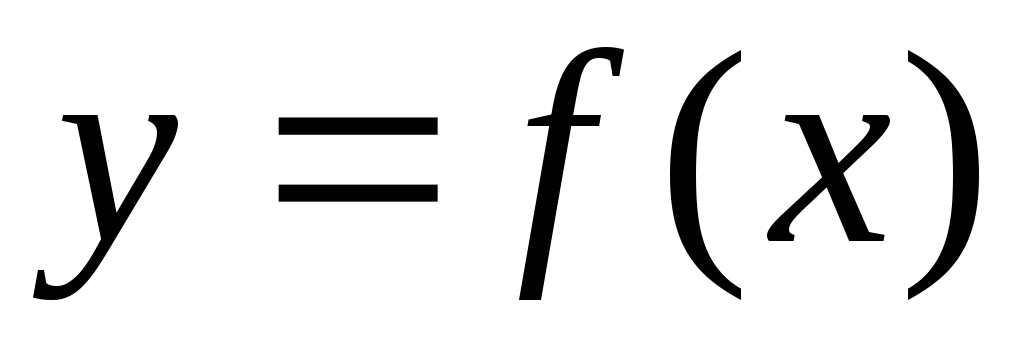 ,
определенная на множестве
,
определенная на множестве
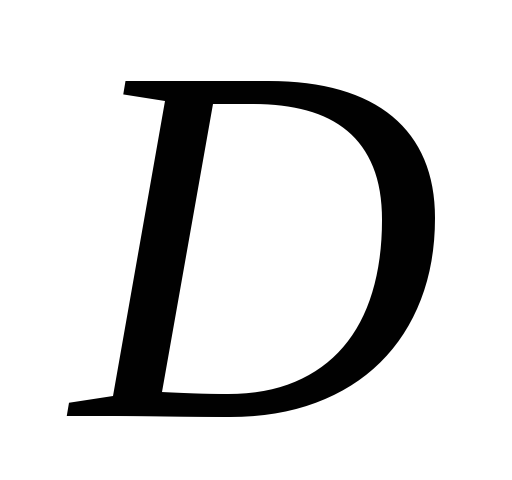 ,
называют ___?___ на этом множестве, если
существует такое число
,
называют ___?___ на этом множестве, если
существует такое число
 ,
что при каждом
,
что при каждом
 значение
значение
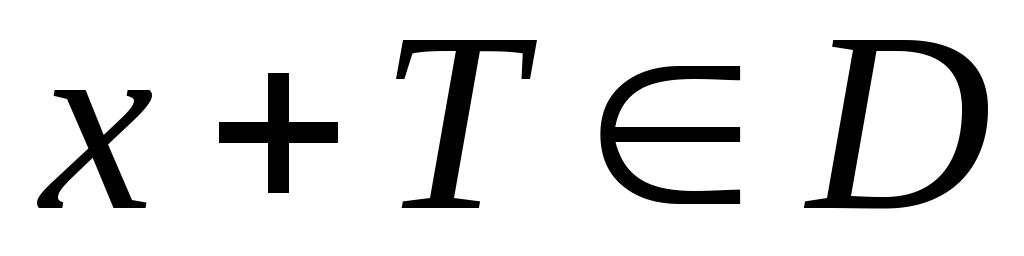 и
и
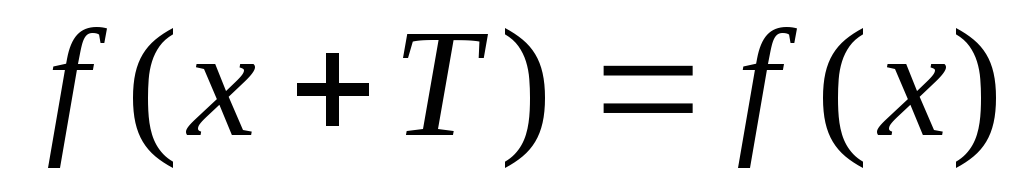 .
. -
Последовательность
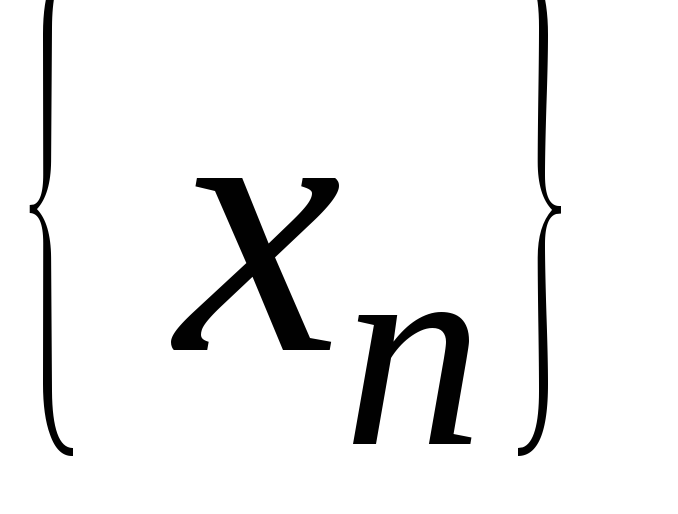 называется ___?___, если существует такое
число
называется ___?___, если существует такое
число
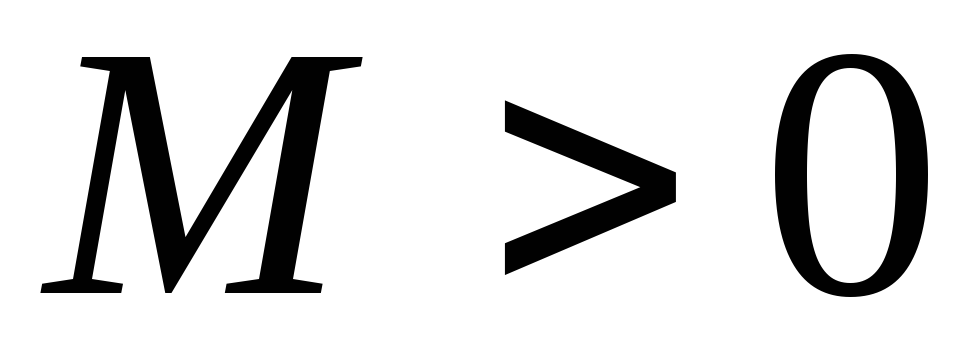 ,
что для любого
,
что для любого
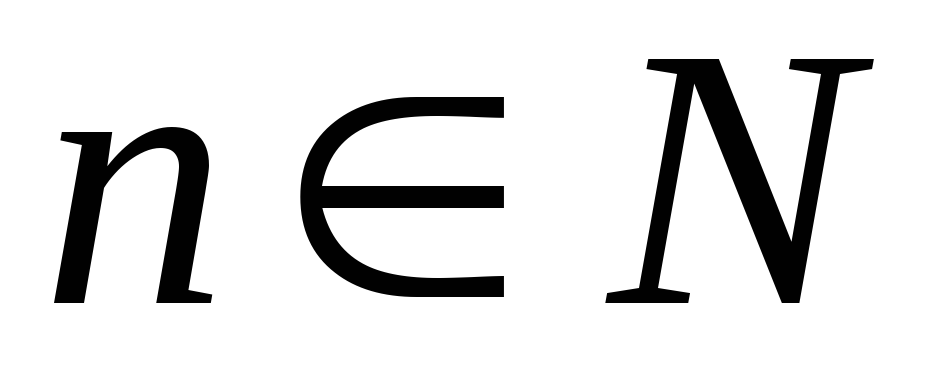 выполняется неравенство
выполняется неравенство
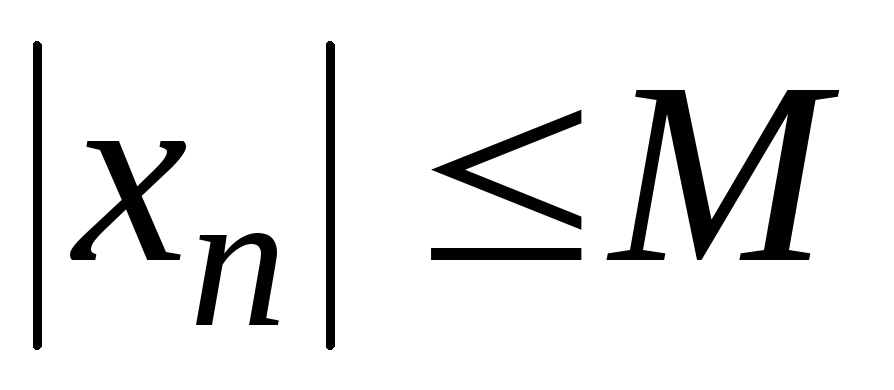 .
. -
Последовательность
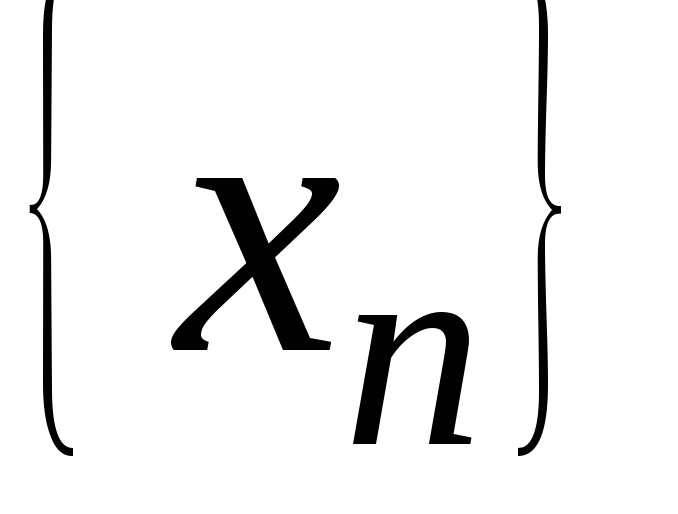 называется ___?___, если для любого
называется ___?___, если для любого
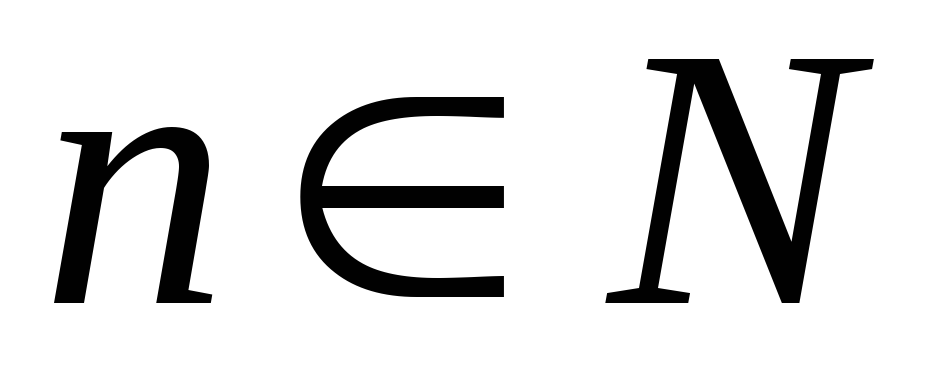 выполняется неравенство
выполняется неравенство
 .
. -
Последовательность
 называется ___?___, если для любого
называется ___?___, если для любого
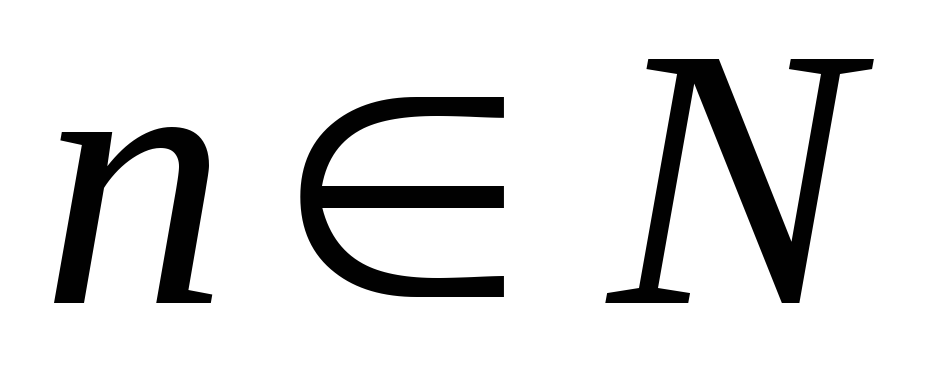 выполняется неравенство
выполняется неравенство
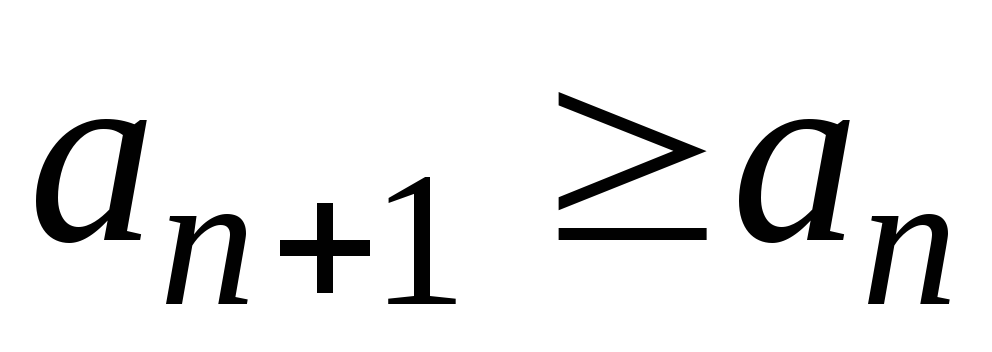 .
. -
Число
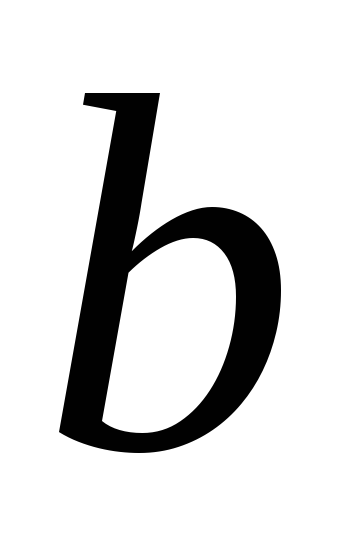 называется пределом числовой
последовательности
называется пределом числовой
последовательности
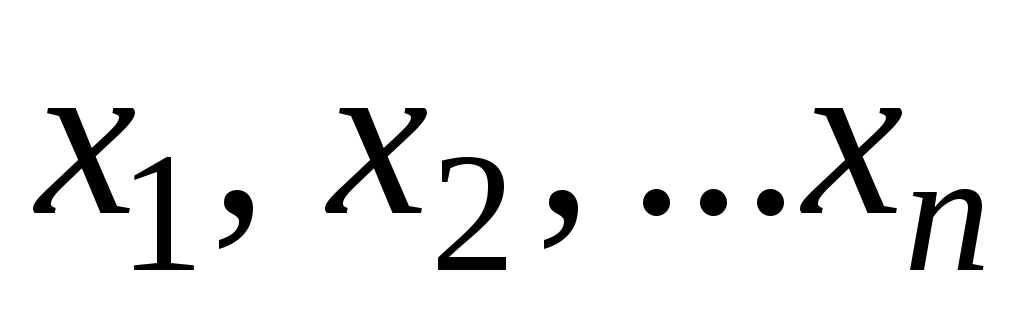 если:
если: -
Число
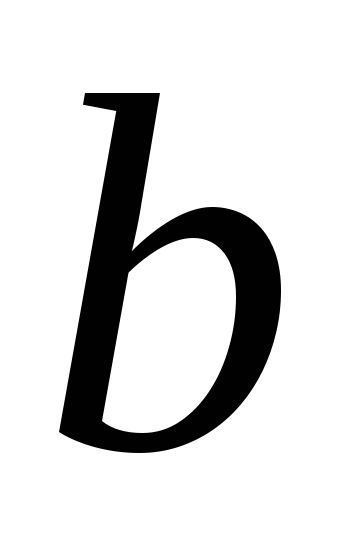 называется пределом числовой
последовательности
называется пределом числовой
последовательности
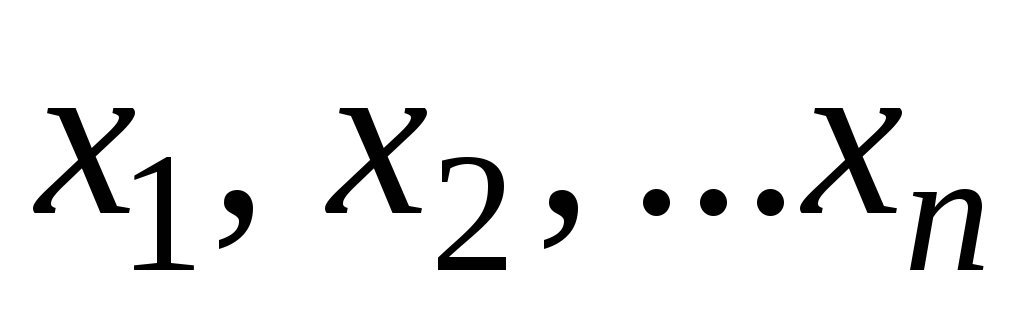 ,
если для любого положительного числа
,
если для любого положительного числа
 найдется такое натуральное число
найдется такое натуральное число
 ,
что при всех
,
что при всех
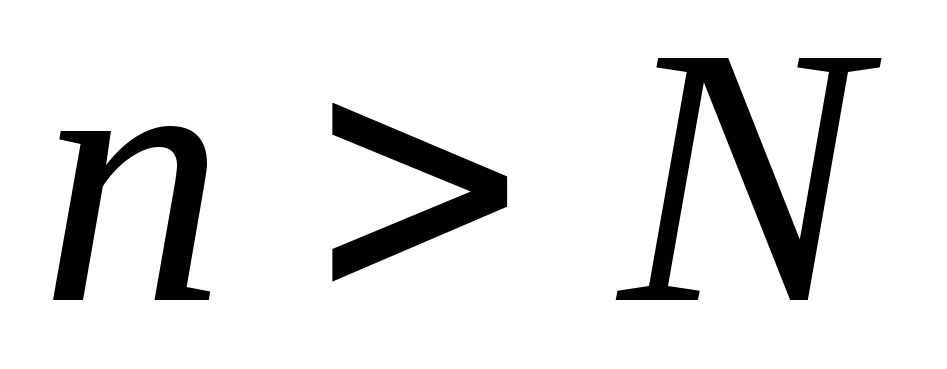 выполняется неравенство:
выполняется неравенство: -
Последовательность, имеющая только один предел называется:
-
Если
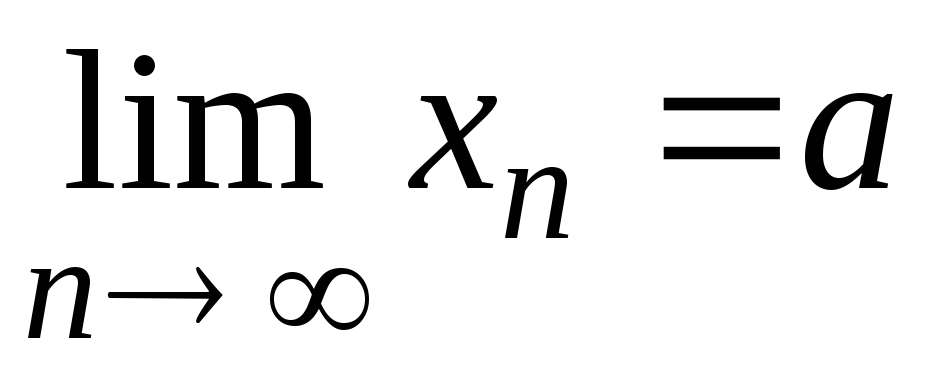 и
и
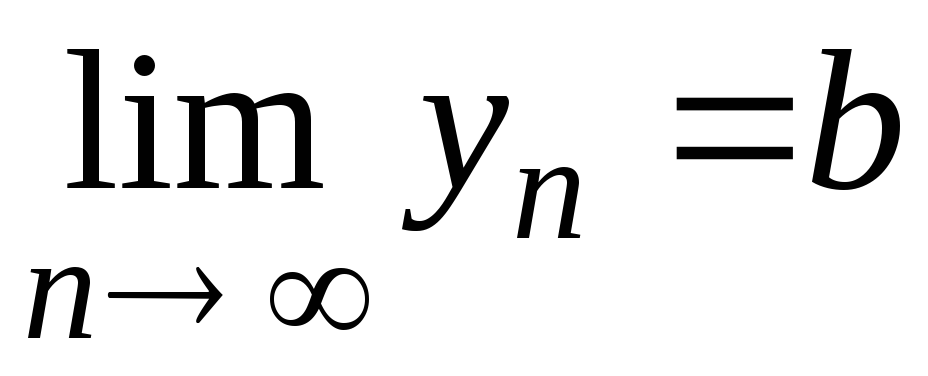 и, начиная с некоторого номера, выполняется
неравенство
и, начиная с некоторого номера, выполняется
неравенство
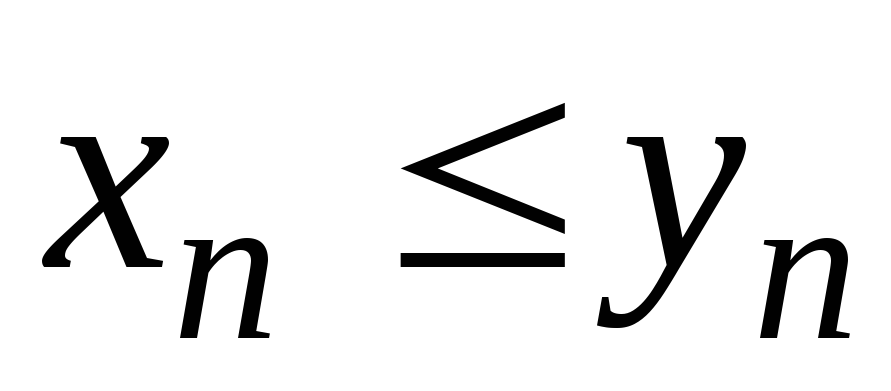 ,
то:
,
то: -
Если
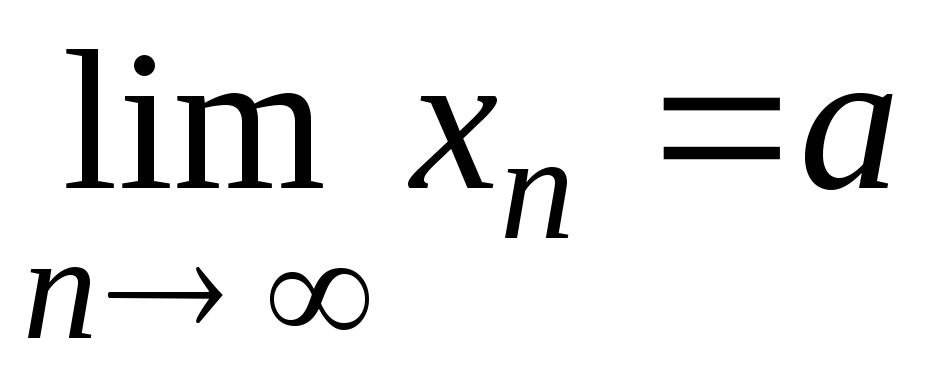
 и справедливо неравенство
и справедливо неравенство
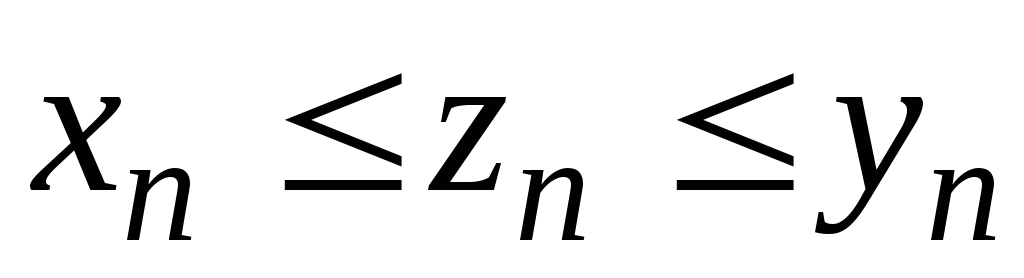 ,
начиная с некоторого номера, то:
,
начиная с некоторого номера, то: -
Теорема Вейерштрасса :
-
Второй замечательный предел:
-
Число
 называется пределом функции
называется пределом функции
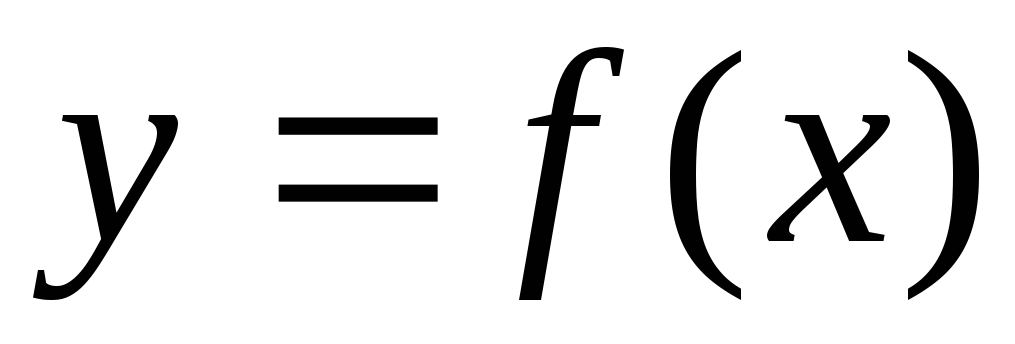 в
точке
в
точке
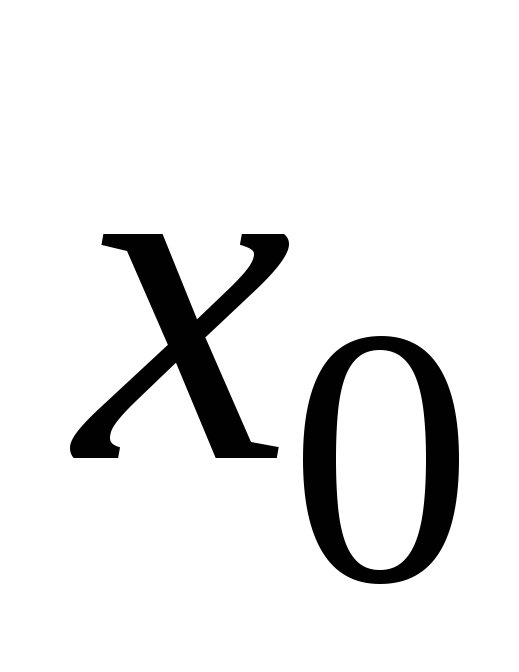 если:
если: -
Число
 называется пределом функции
называется пределом функции
 в
точке
в
точке
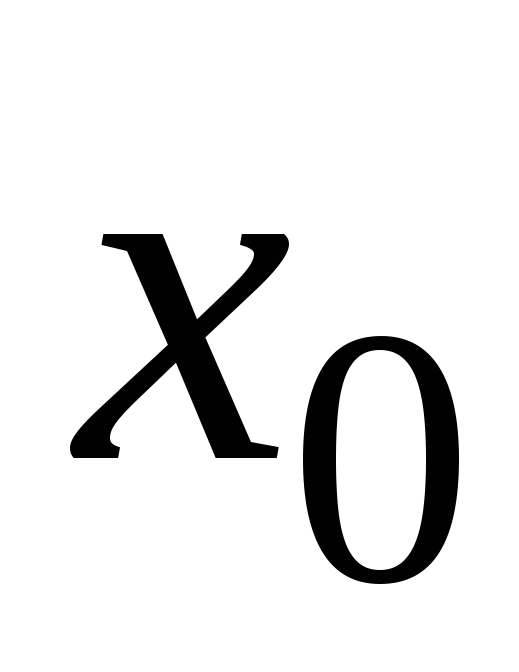 если:
если: -
Число
 называется пределом функции
называется пределом функции
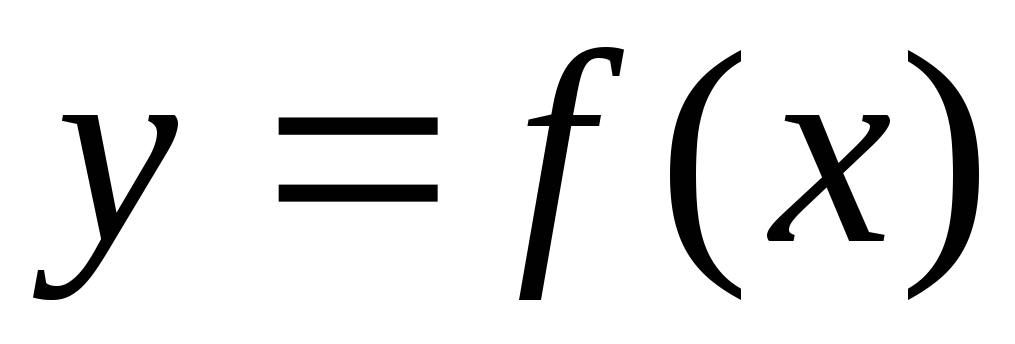 слева в точке
слева в точке
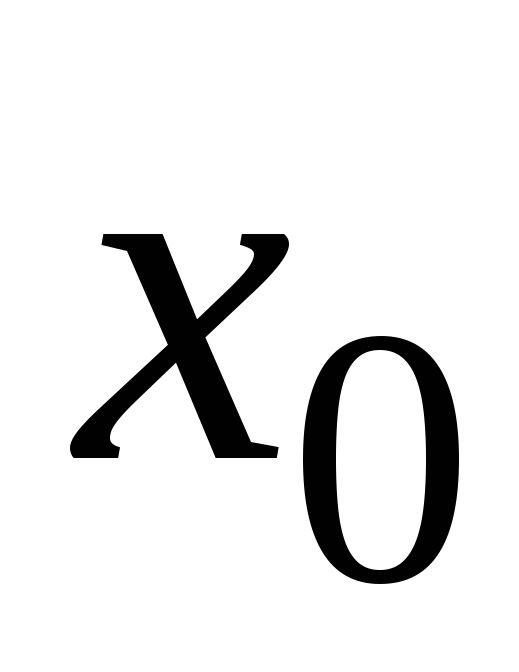 если:
если: -
Число
 называется пределом функции
называется пределом функции
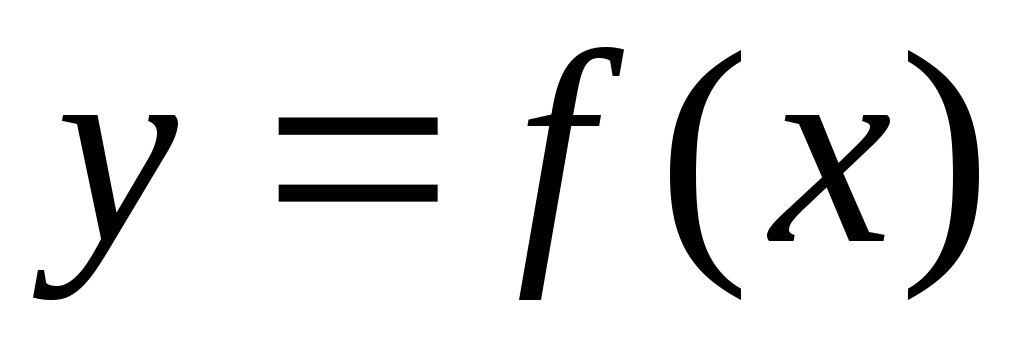 справа в точке
справа в точке
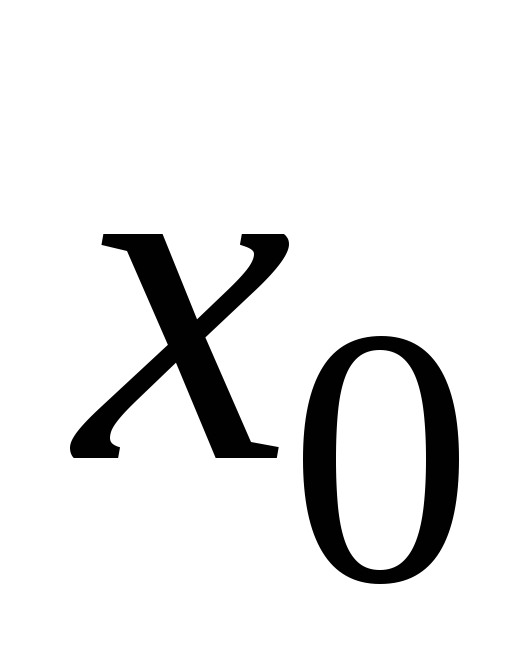 если:
если: -
Число
 называется пределом функции
называется пределом функции
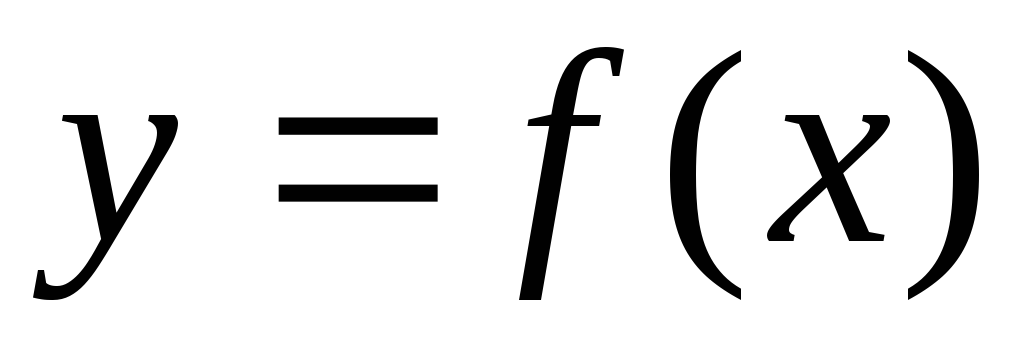 при
при
 если:
если: -
Функция называется бесконечно большой при
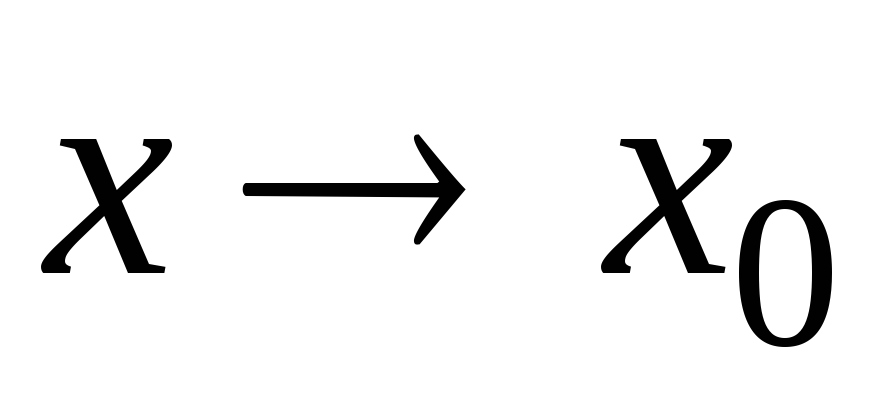 ,
если:
,
если: -
Функция называется бесконечно большой при
 ,
если:
,
если: -
Функция называется бесконечно малой при
 ,
если:
,
если: -
Выберите НЕ верное утверждение:
-
Если функция
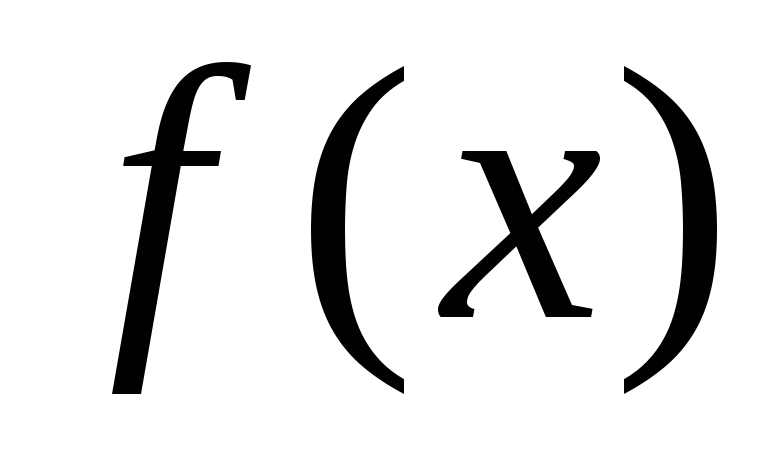 имеет предел, равный
имеет предел, равный
 ,
то ее можно представить в виде:
,
то ее можно представить в виде: -
Выберите НЕ верную теорему о пределах:
-
Теорема о пределе монотонной функции:
-
Последовательность имеет предел если она:
-
Первый замечательный предел:
-
Пусть
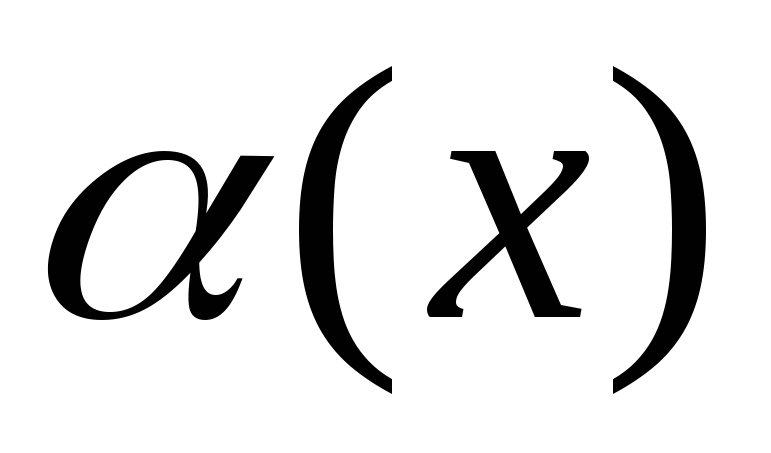 и
и
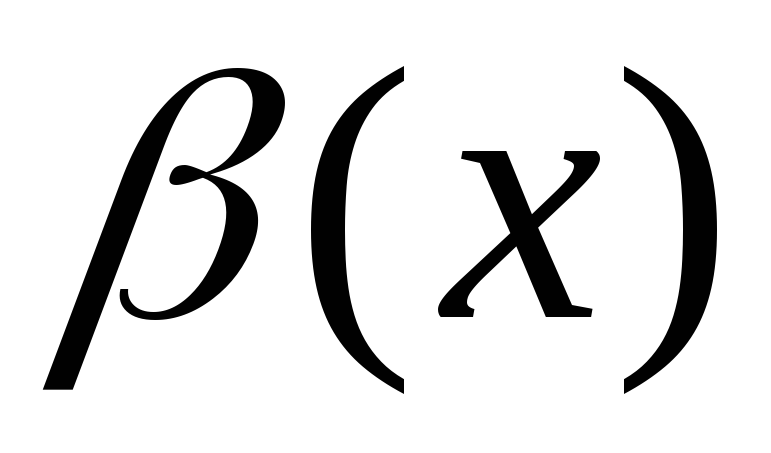 есть бесконечно малые функции при
есть бесконечно малые функции при
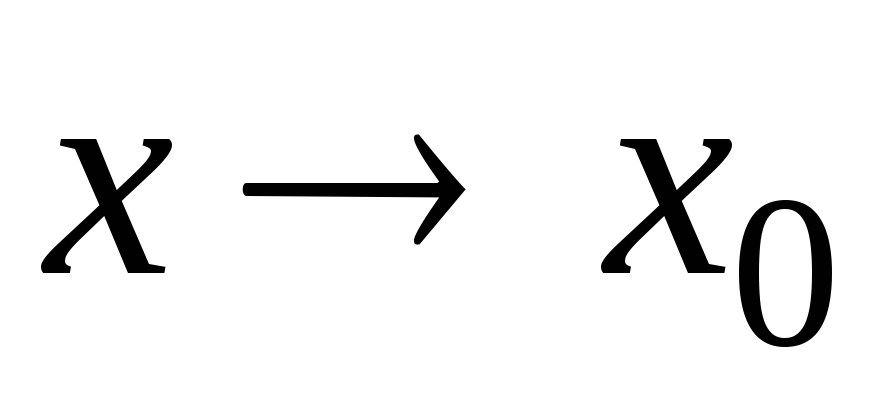 ,
тогда:
,
тогда: -
Выберите НЕ верную теорему о бесконечно малых:
-
Функция
 называется непрерывной в точке
называется непрерывной в точке
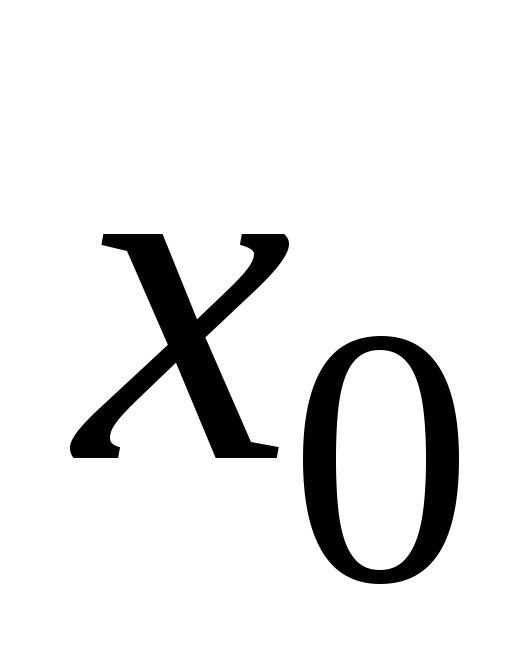 ,
если:
,
если: -
Функция
 называется непрерывной на отрезке
называется непрерывной на отрезке
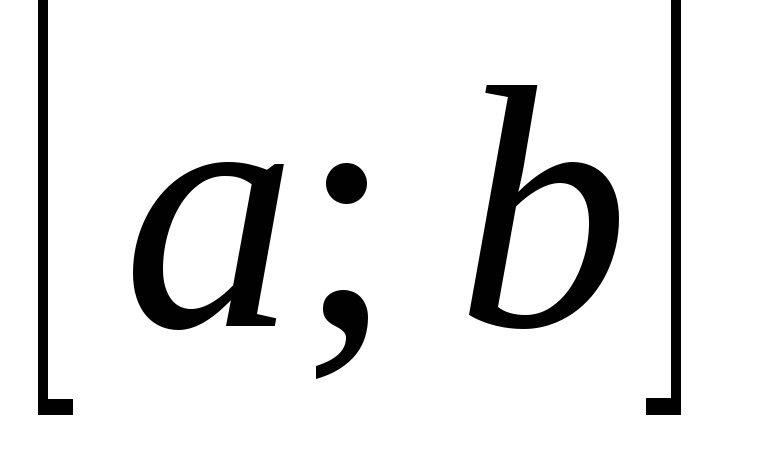 если:
если: -
Точками разрыва функции называют точки в которых:
-
Функция имеет разрыв первого рода если выполнено:
-
Функция имеет разрыв второго рода если выполнено:
-
Выберите НЕ верную теорему о непрерывных функциях:
-
Продолжите теорему: пусть функция
 непрерывна в точке
непрерывна в точке
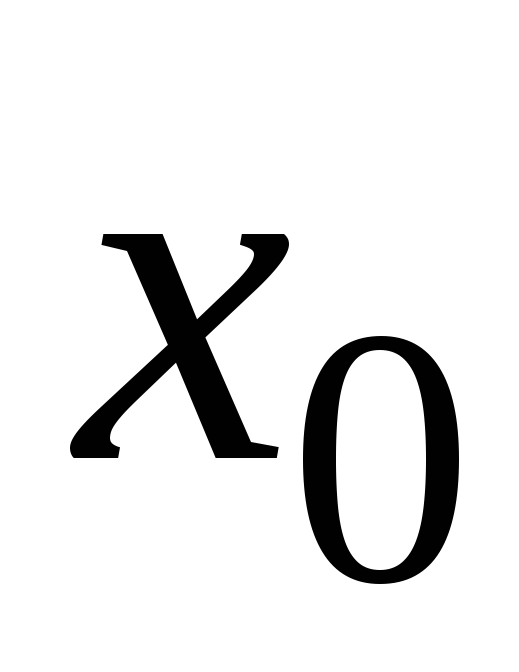 ,
а функция
,
а функция
 ,
непрерывна в точке
,
непрерывна в точке
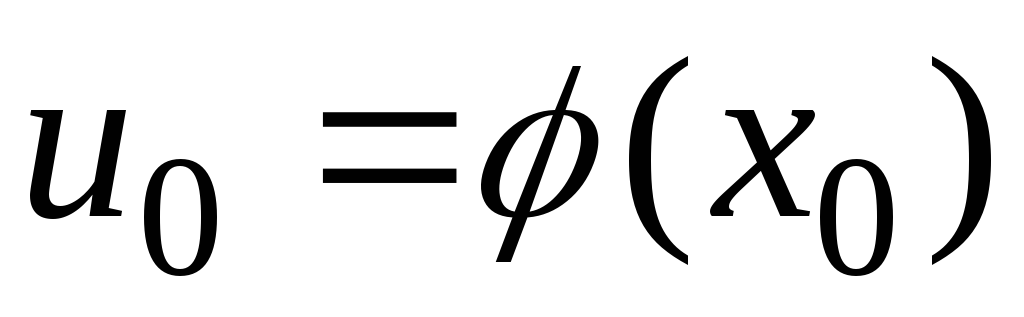 .
Тогда сложная функция
.
Тогда сложная функция
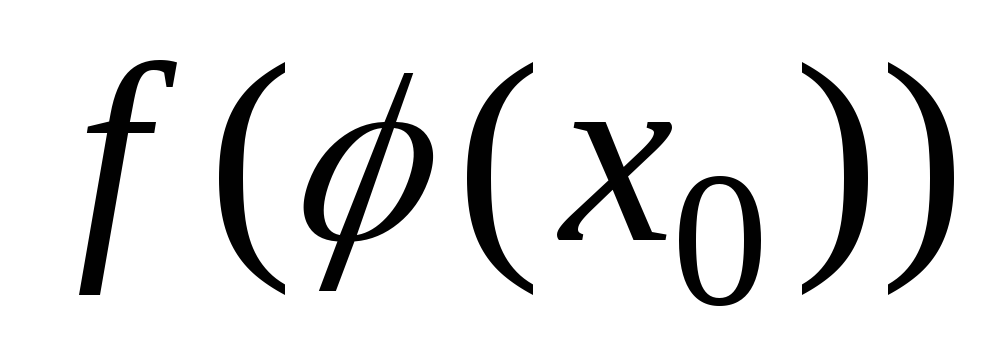 ,
состоящая из непрерывных функций:
,
состоящая из непрерывных функций: -
Продолжите теорему: если функция
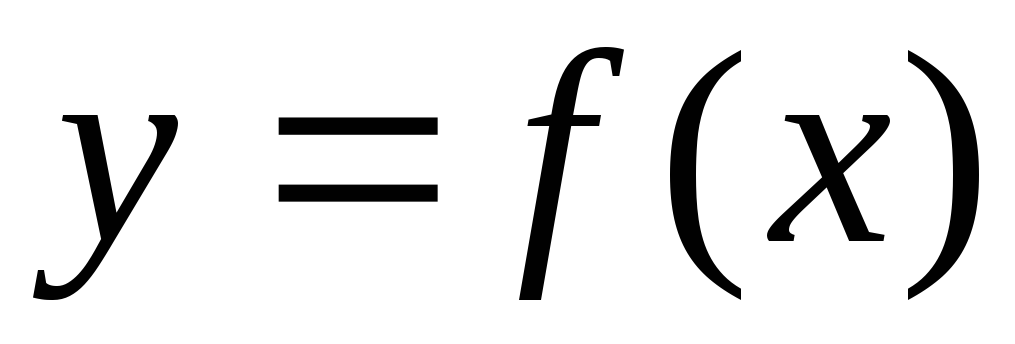 непрерывна и строго монотонна на
непрерывна и строго монотонна на
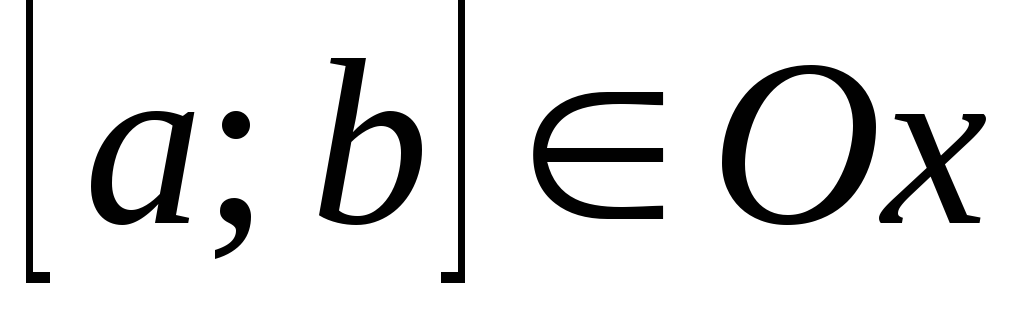 ,
то обратная функция
,
то обратная функция
 :
: -
Какими свойствами обладает непрерывная на отрезке функция:
-
Касательной к данной кривой в данной точке
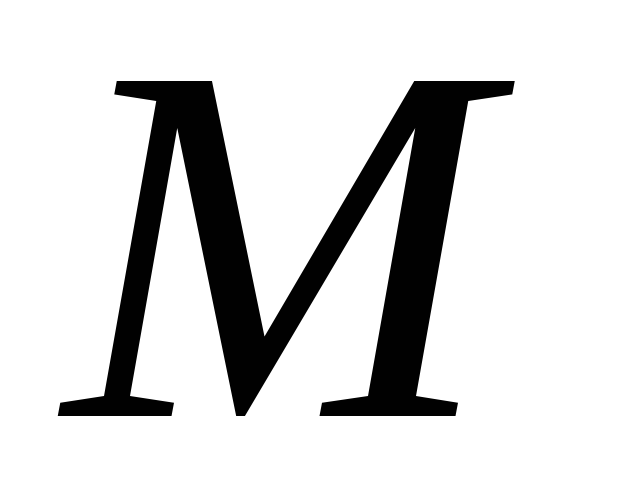 называется:
называется: -
Производной функции
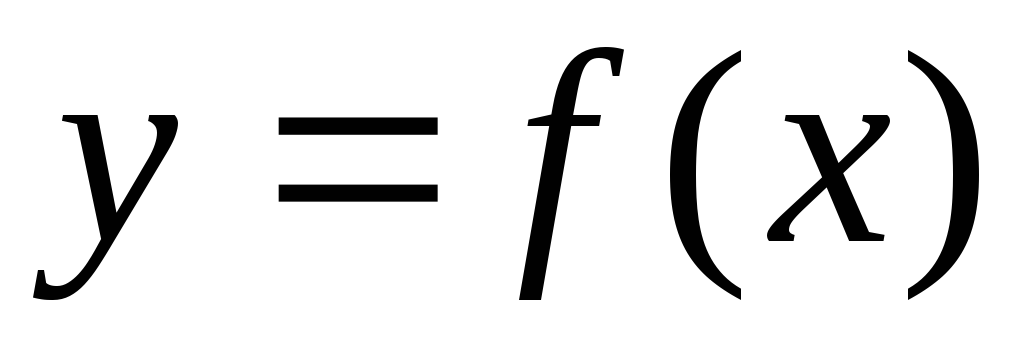 в точке
в точке
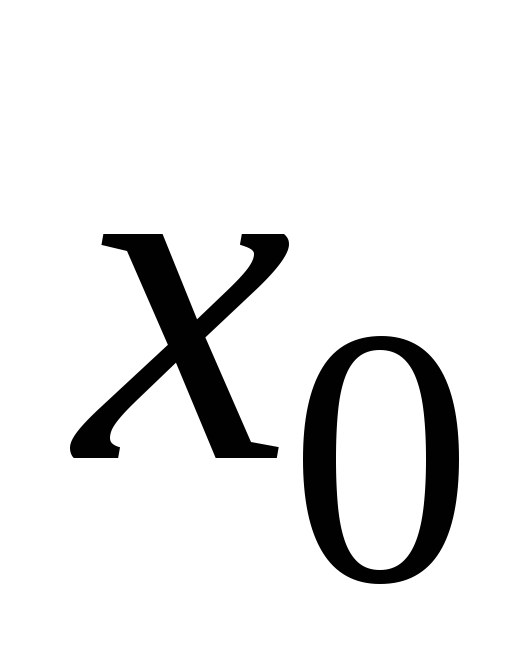 называется:
называется: -
Операция нахождения производной функции называется:
-
Геометрический смысл производной:
-
Уравнение касательной к графику функции имеет вид:
-
Уравнение нормали к графику функции имеет вид:
-
Выберите верное утверждение:
-
Правила дифференцирования:
-
Если функция
 имеет производную
имеет производную
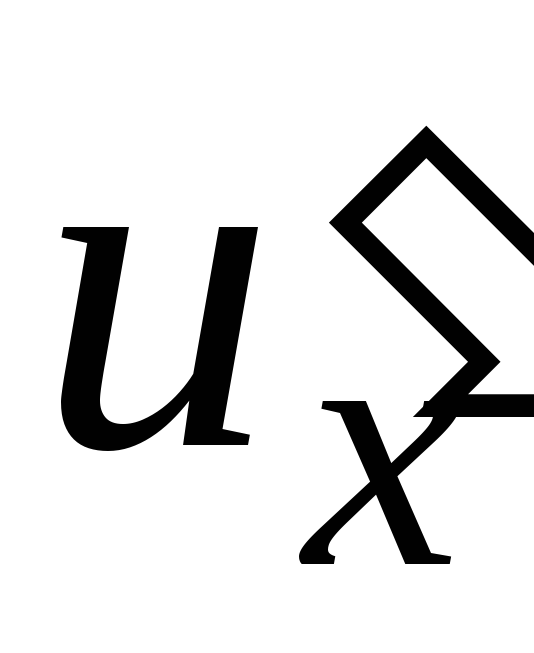 в точке
в точке
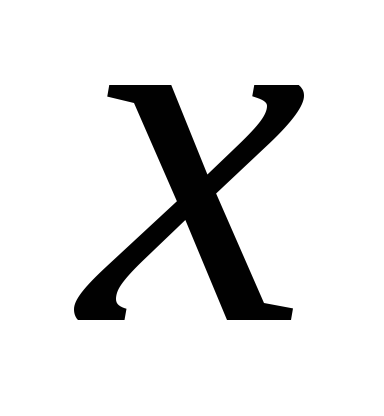 ,
а функция
,
а функция
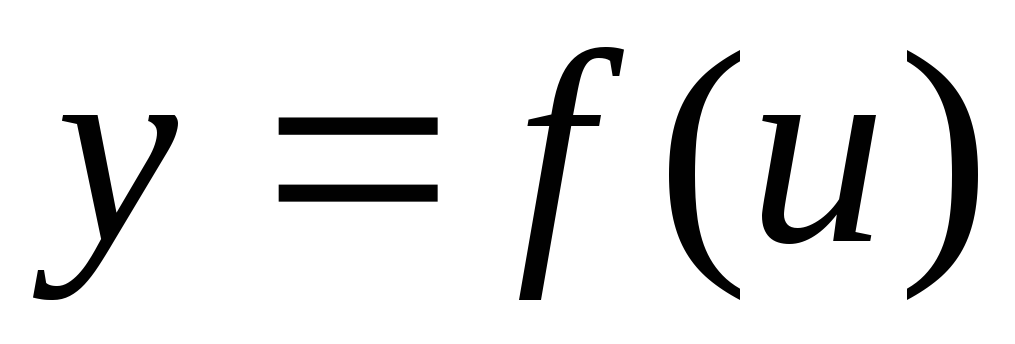 ,
имеет производную
,
имеет производную
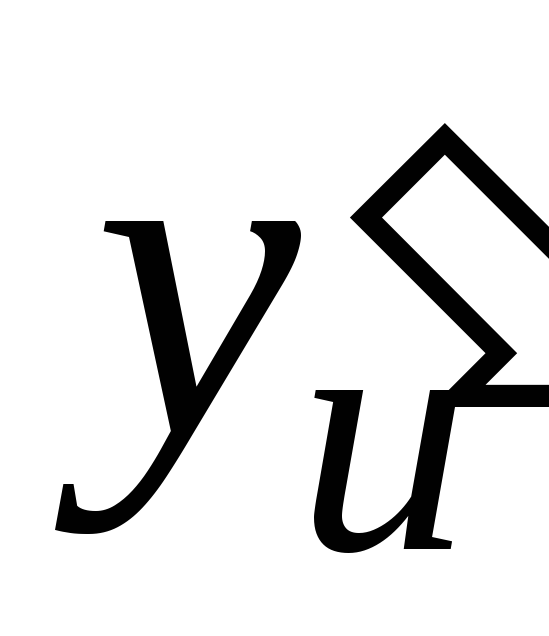 в точке
в точке
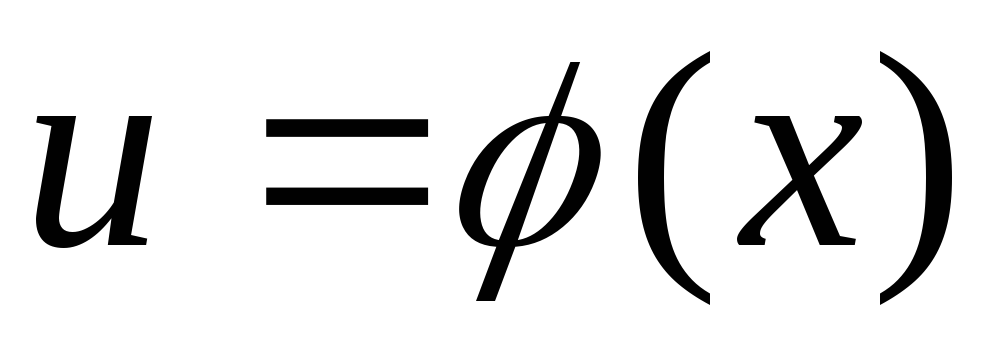 ,
то сложная функция
,
то сложная функция
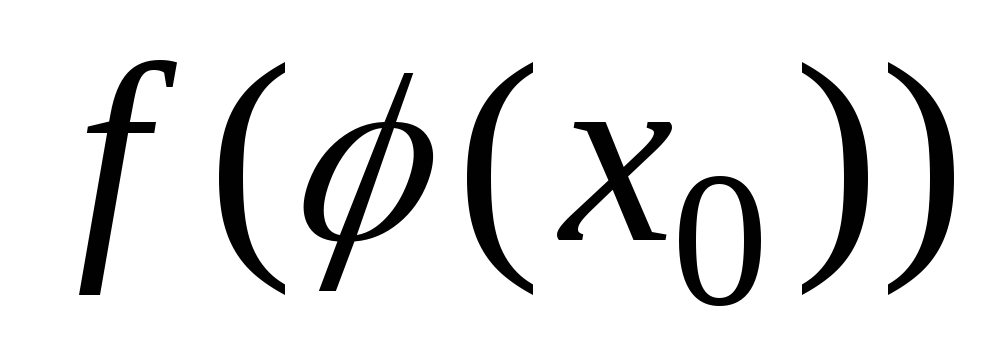 :
: -
Если функция
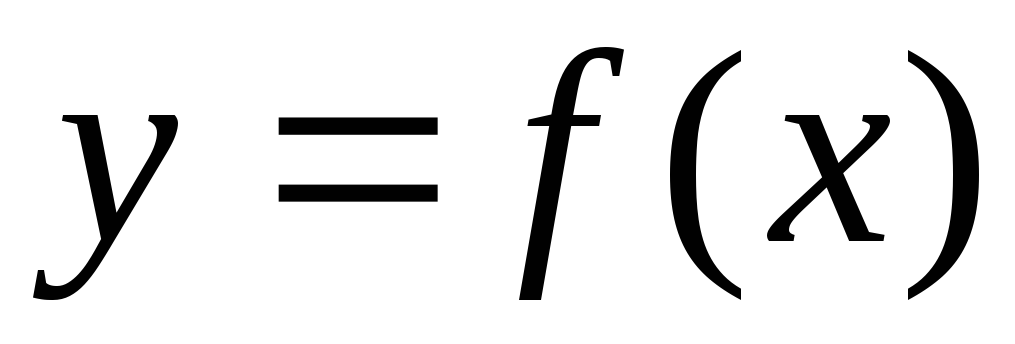 строго монотонна на интервале
строго монотонна на интервале
 и имеет неравную нулю производную
и имеет неравную нулю производную
 в произвольной точке этого интервала,
то обратная функция
в произвольной точке этого интервала,
то обратная функция
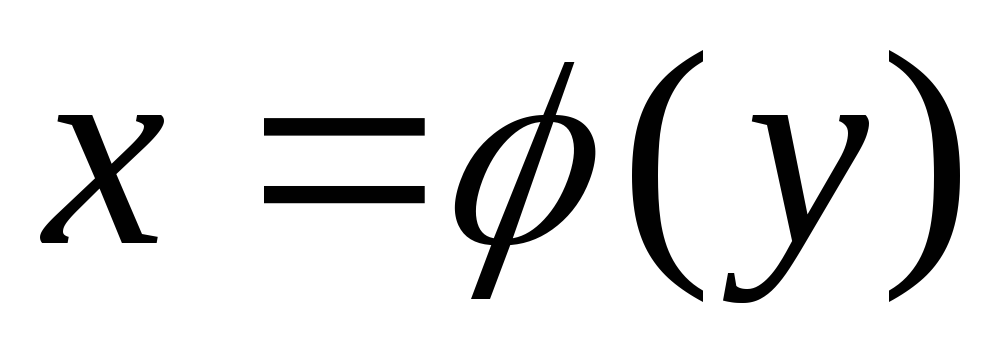 также
имеет производную
также
имеет производную
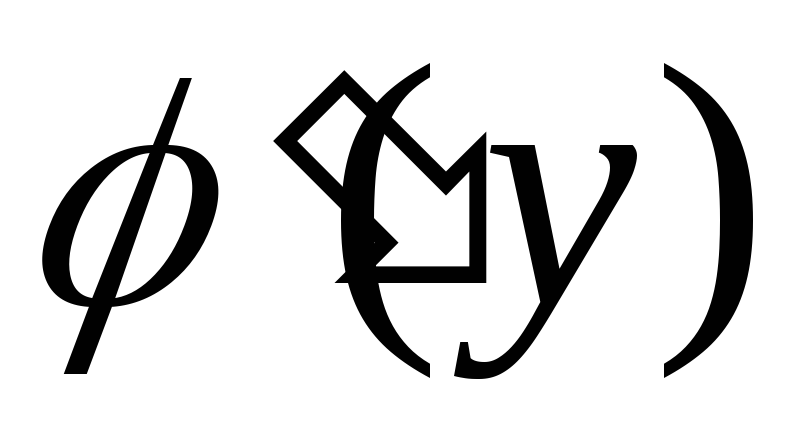 в соответствующей точке определяемую
равенством:
в соответствующей точке определяемую
равенством: -
производные основных функций:
-
Под неявным заданием функции понимают задание функции в виде уравнения:
-
Под параметрическим заданием функции понимают задание функции в виде уравнения:
-
Производная пятого порядка обозначается:
-
Производная второго порядка параметрически заданной функции вычисляется по формуле:
-
Дифференциалом функции называется:
-
геометрический смысл дифференциала функции:
-
Для вычисления приближенных значений функции применяют формулу:
-
Дифференциал высших порядков:
-
Если функция
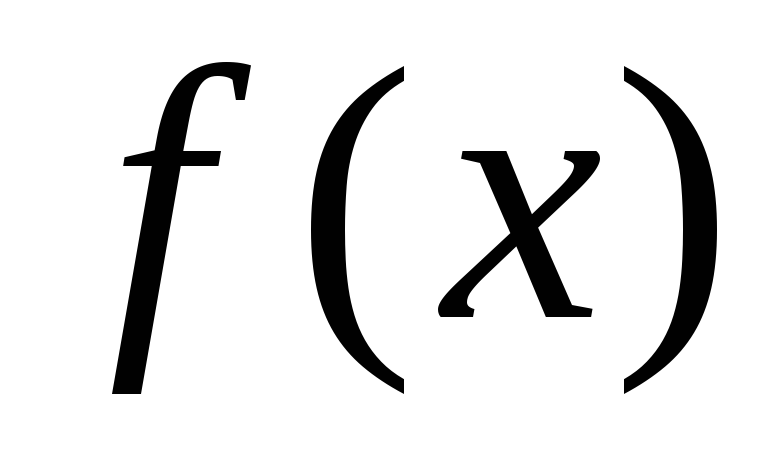 непрерывна на отрезке
непрерывна на отрезке
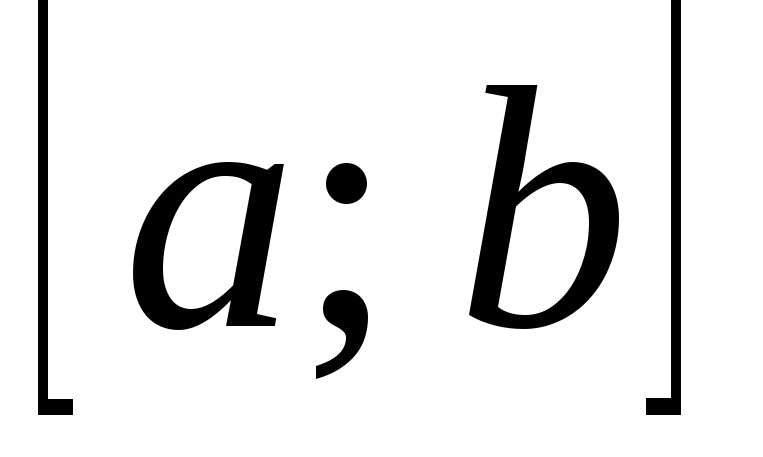 дифференцируема на интервале
дифференцируема на интервале
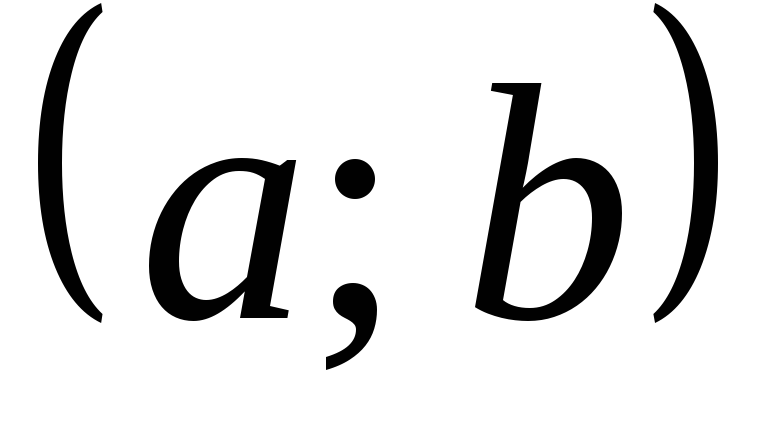 и на концах отрезка принимает одинаковые
значения
и на концах отрезка принимает одинаковые
значения
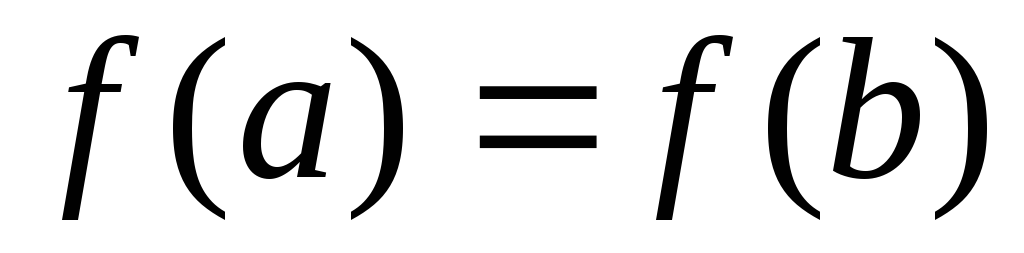 ,
то найдется хотя бы одна точка
,
то найдется хотя бы одна точка
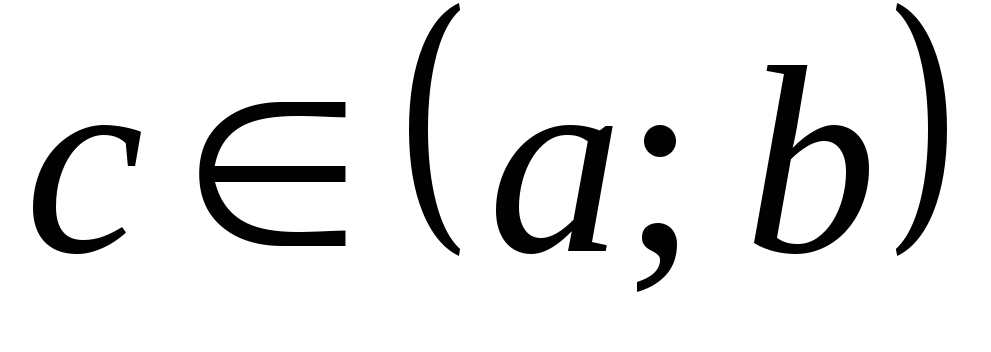 ,
в которой производная
,
в которой производная
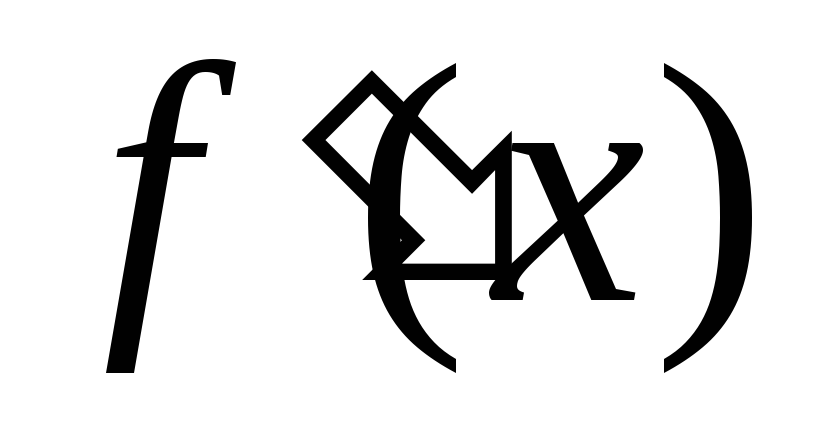 обращается
в нуль.
обращается
в нуль. -
Если функции
 и
и
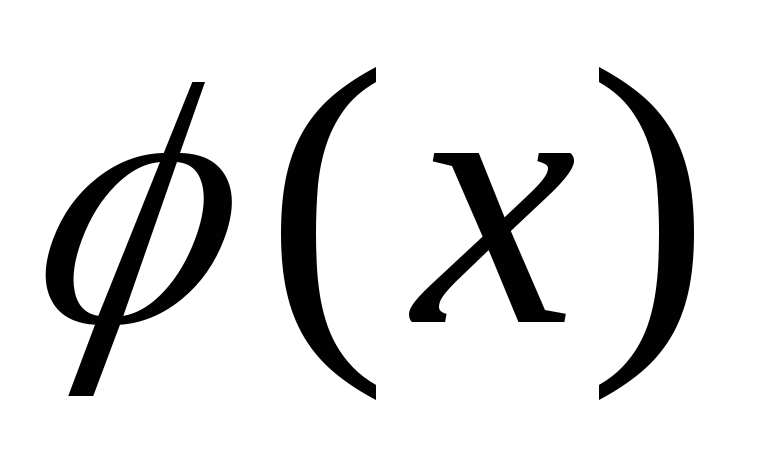 непрерывны на отрезке
непрерывны на отрезке
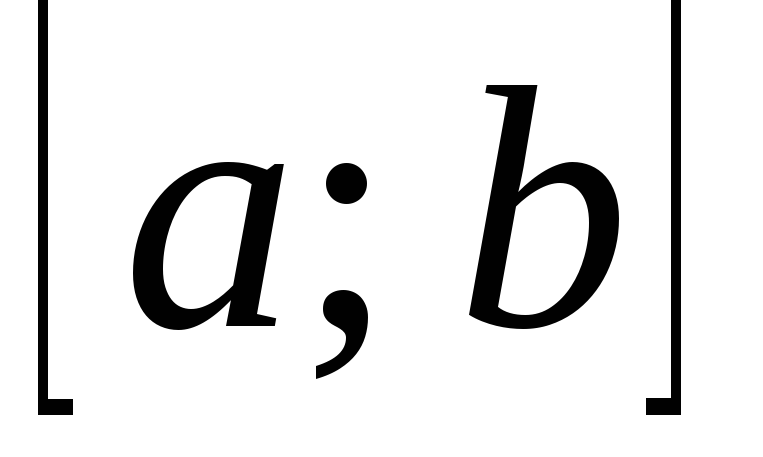 ,
дифференцируемы на интервале
,
дифференцируемы на интервале
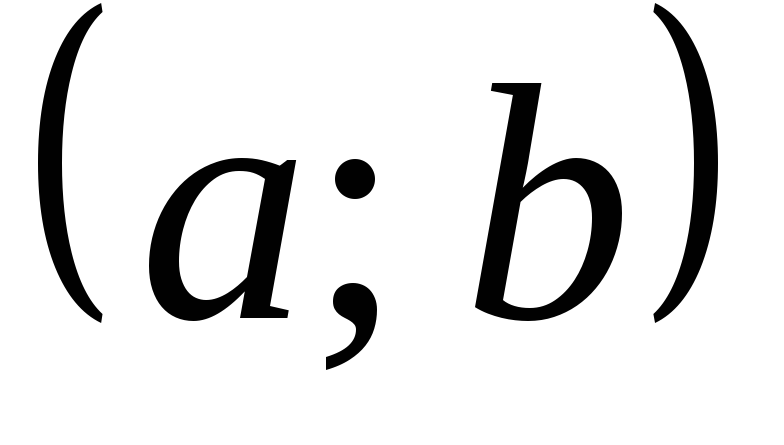 ,
то найдется хотя бы одна точка
,
то найдется хотя бы одна точка
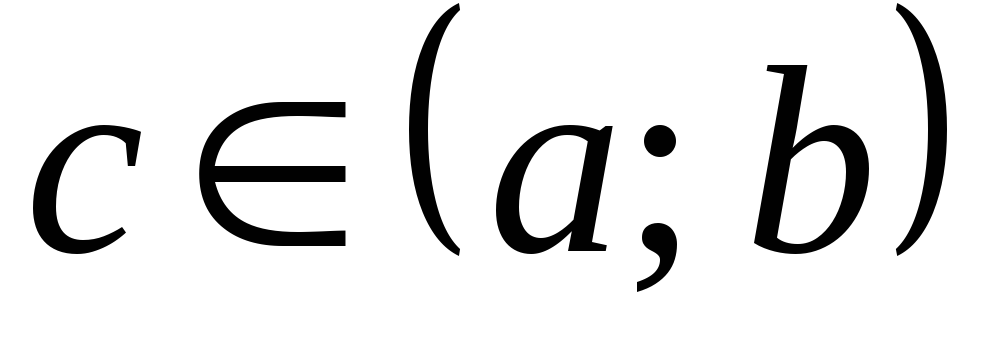 такая, что выполняется равенство
такая, что выполняется равенство
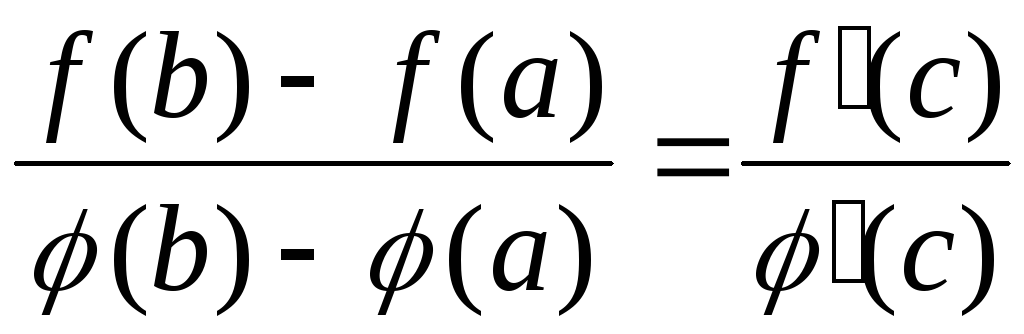 :
: -
Свойство инвариантности дифференциала функции:
-
Если функция
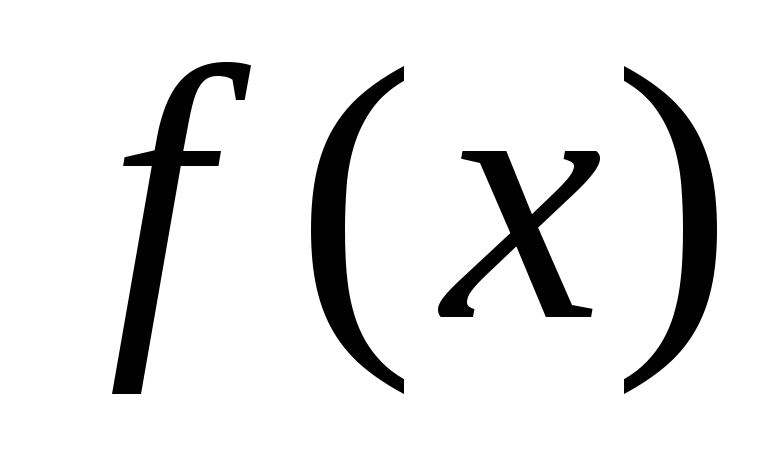 непрерывна на отрезке
непрерывна на отрезке
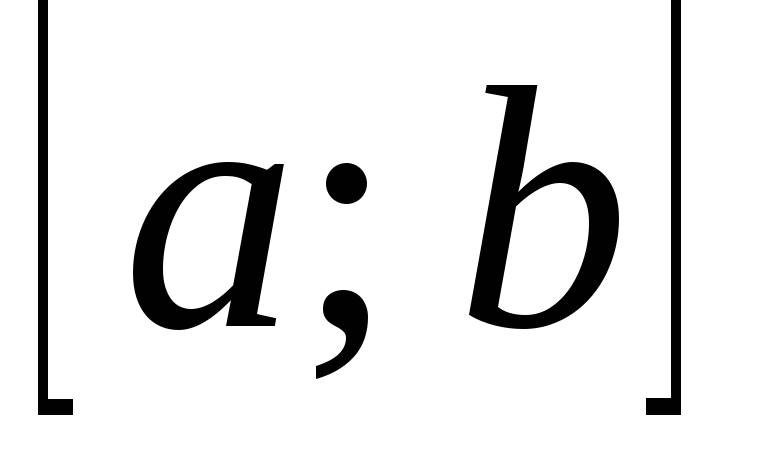 дифференцируема на интервале
дифференцируема на интервале
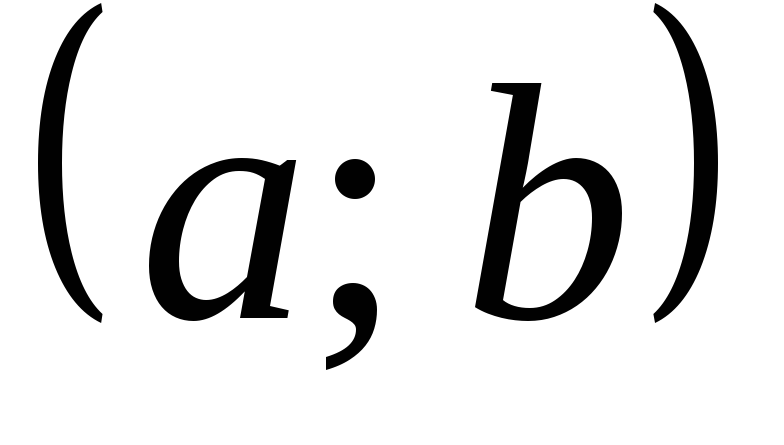 ,
то найдется хотя бы одна точка
,
то найдется хотя бы одна точка
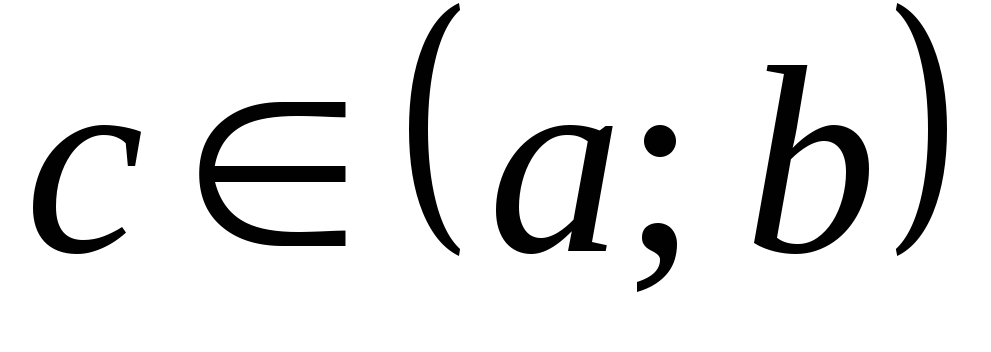 такая, что выполняется равенство
такая, что выполняется равенство

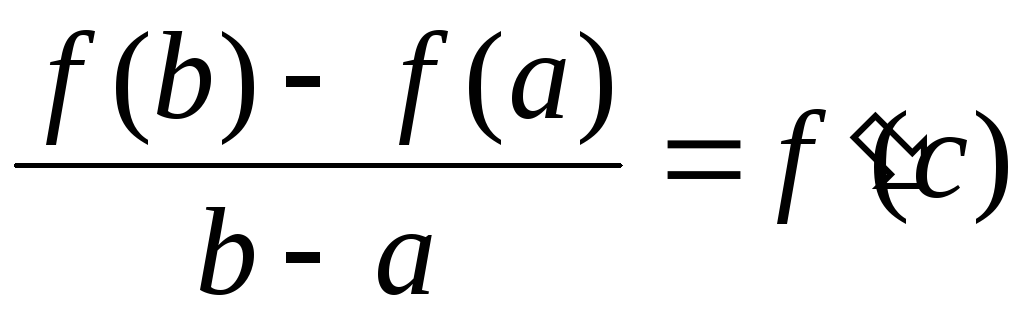 .
. -
Пусть функции
 и
и
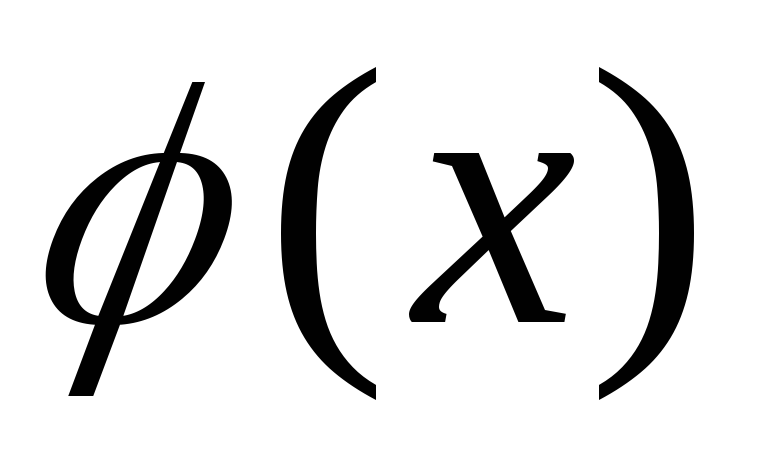 непрерывны и дифференцируемы в
окрестности точки
непрерывны и дифференцируемы в
окрестности точки
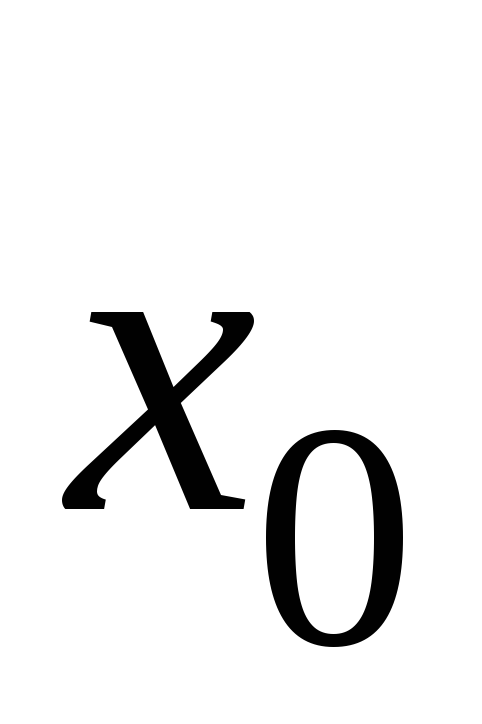 и обращаются в нуль в этой точке и
и обращаются в нуль в этой точке и
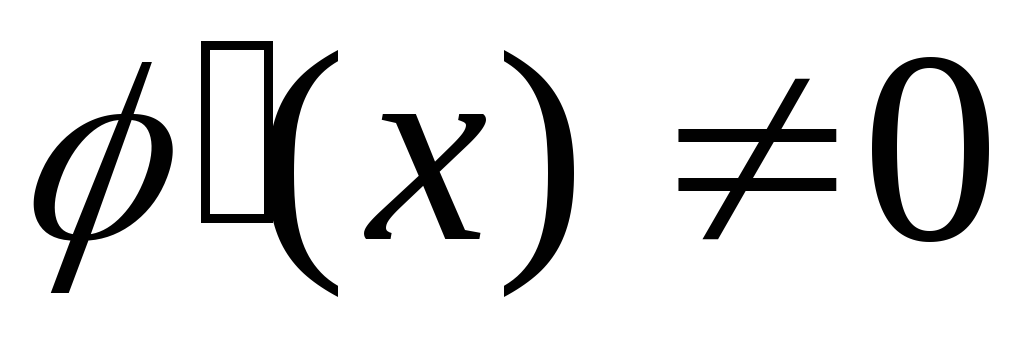 в окрестности точки
в окрестности точки
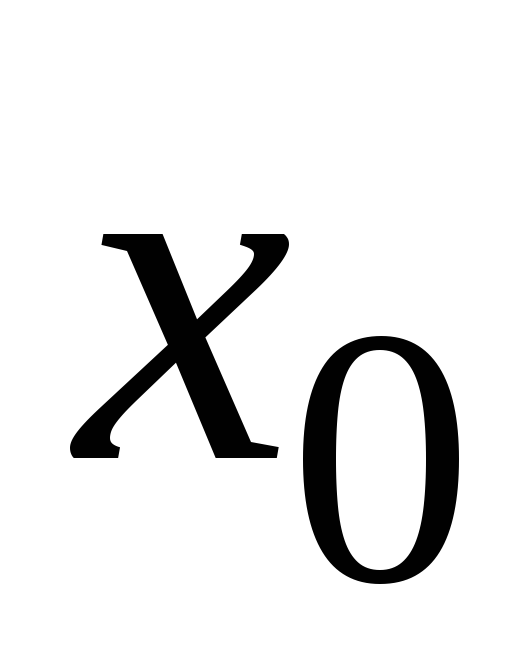 .
Если существует предел
.
Если существует предел
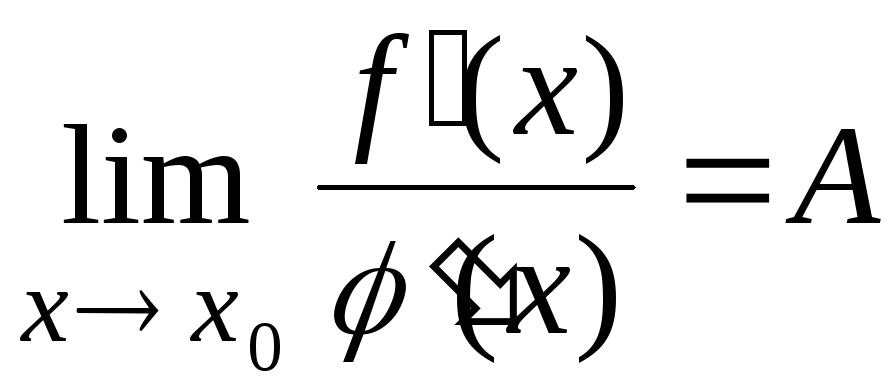 ,
то
,
то
 .
. -
Пусть функции
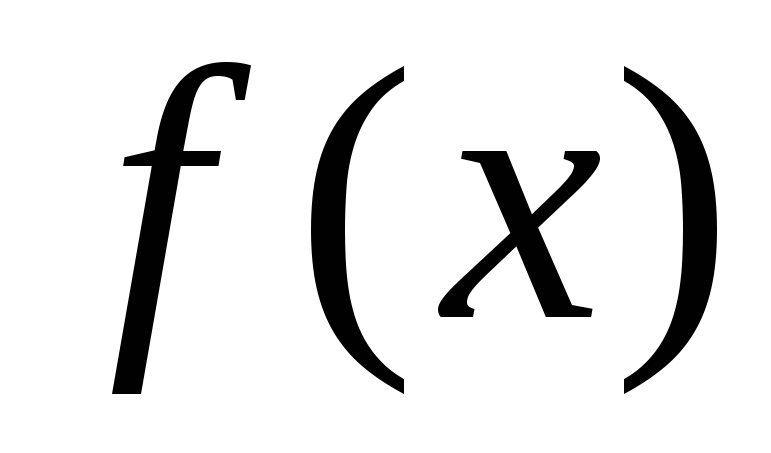 и
и
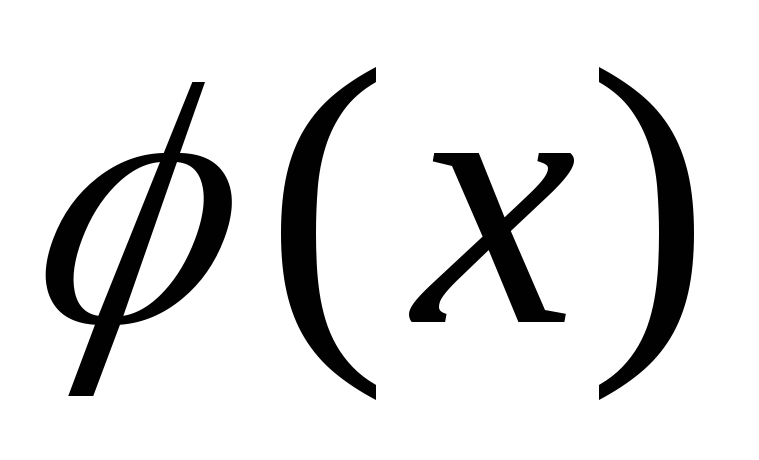 непрерывны и дифференцируемы в
окрестности точки
непрерывны и дифференцируемы в
окрестности точки
 и равны бесконечности в этой точке и
и равны бесконечности в этой точке и
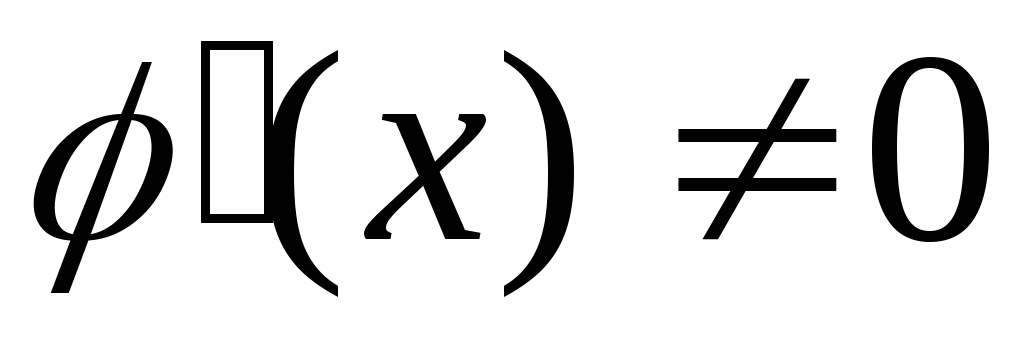 в окрестности точки
в окрестности точки
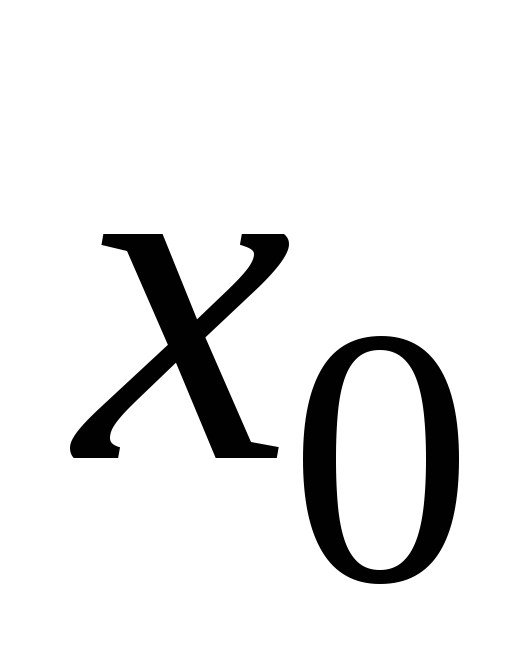 .
Если существует предел
.
Если существует предел
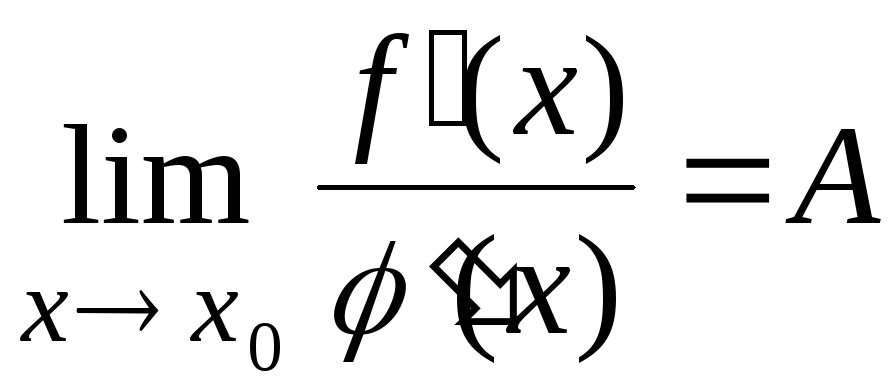 ,
то
,
то
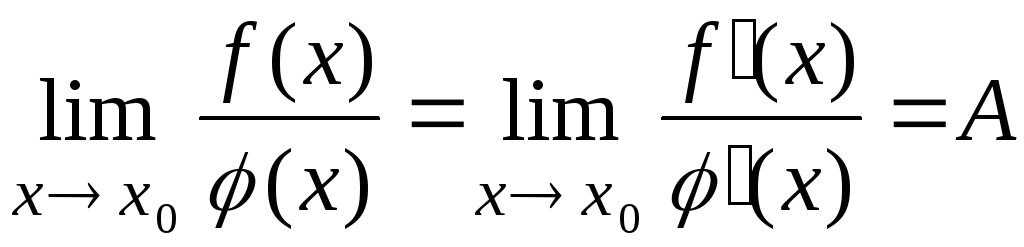 .
. -
Необходимое условие возрастания функции:
-
Достаточное условие возрастания функции:
-
Необходимое условие убывания функции:
-
Достаточное условие убывания функции:
-
Необходимое условие существования экстремума функции:
-
Достаточное условие существования экстремума функции:
-
Экстремальными точками функции называются точки:
-
Достаточное условие существования экстремума функции:
-
График функции называется выпуклым вниз на интервале
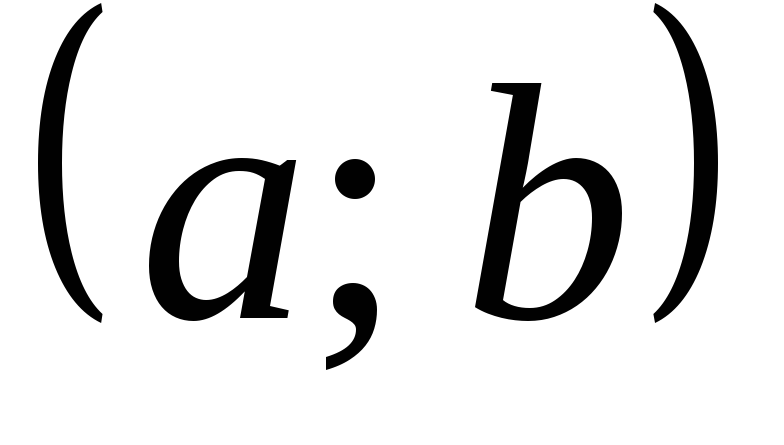 ,
если:
,
если: -
График функции называется выпуклым вверх на интервале
 ,
если:
,
если: -
Достаточное условие существование точек перегиба:
-
Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремиться к нулю:
-
Говорят, что прямая
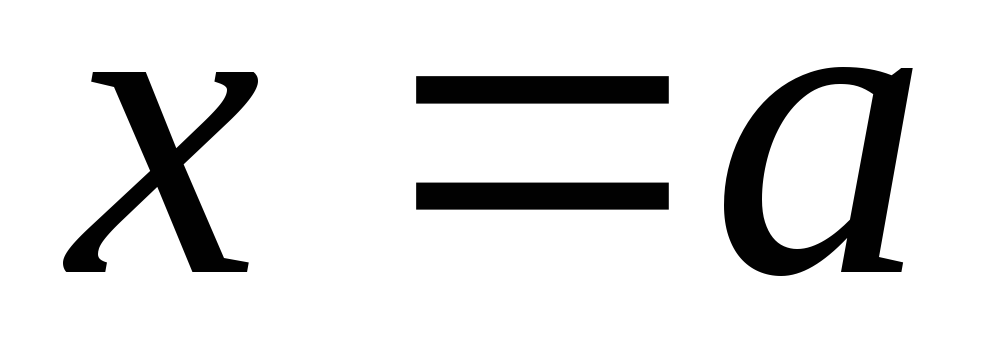 является вертикальной асимптотой
графика функции
является вертикальной асимптотой
графика функции
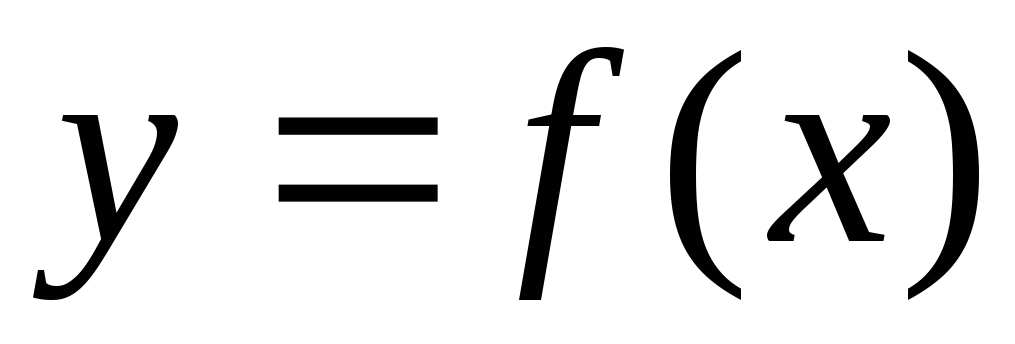 ,
если:
,
если: -
Уравнение наклонной асимптоты ищем в виде
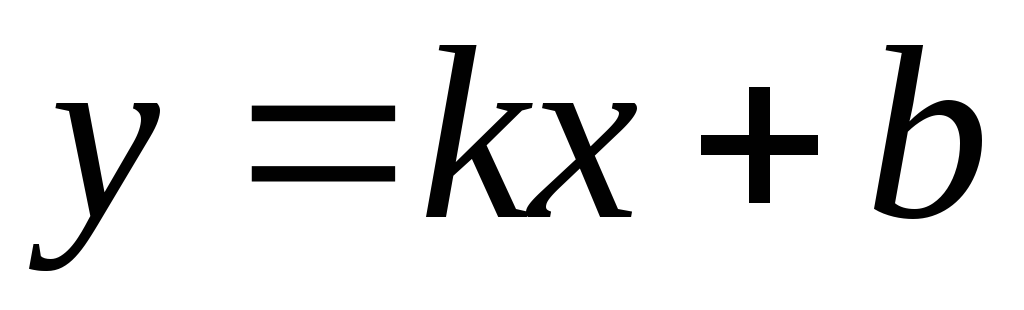 ,
где
,
где
 и
и
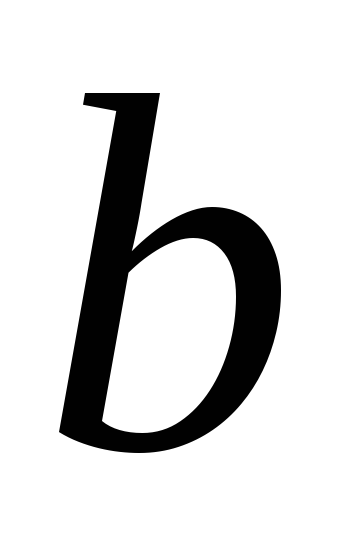 вычисляются по формуле:
вычисляются по формуле: -
Многочленом Тейлора для функции
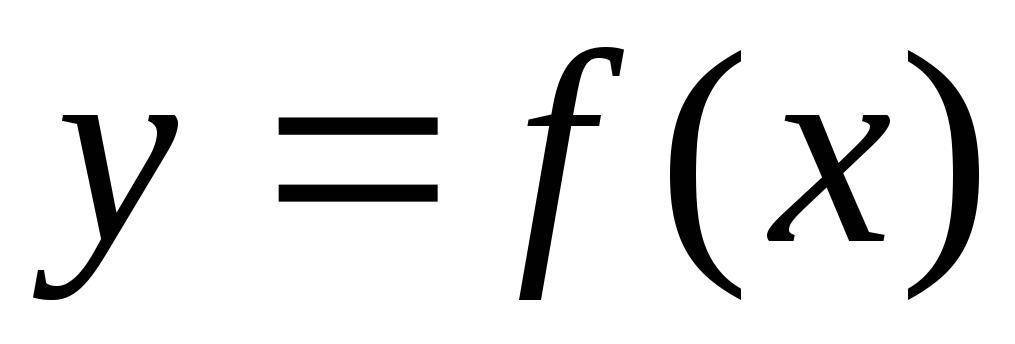 называется выражение:
называется выражение: -
Многочленом Маклорена для функции
 называется выражение:
называется выражение: -
Функция
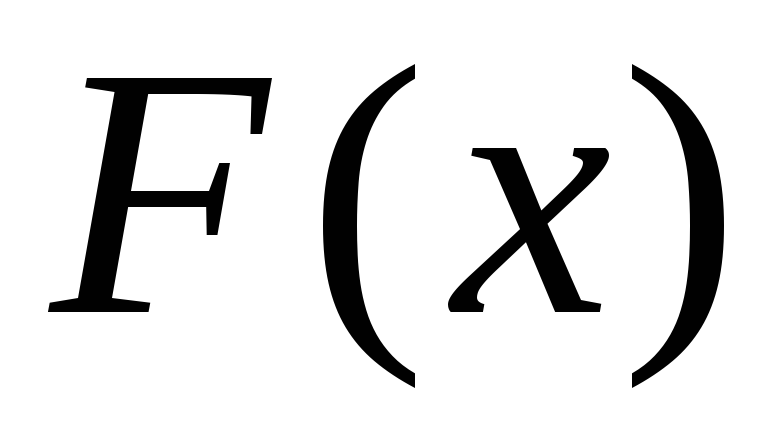 называется
первообразной функции
называется
первообразной функции
 на интервале
на интервале
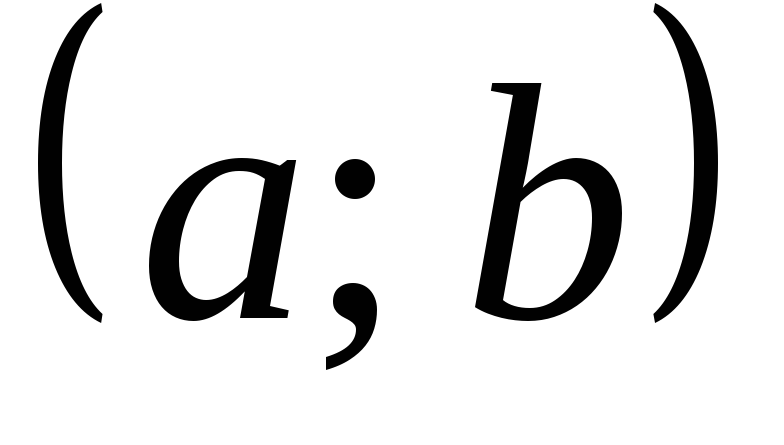 ,
если для любого
,
если для любого
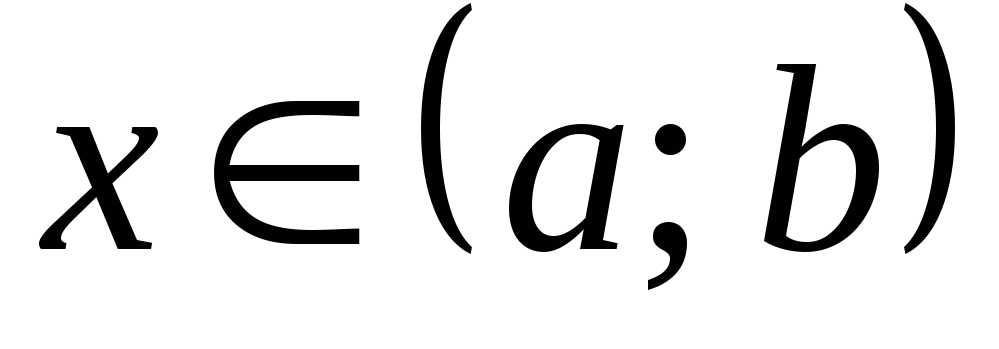 выполняется равенство:
выполняется равенство: -
График первообразной называется:
-
Свойства неопределенного интеграла это:
-
Формула
 называется:
называется: -
Формула
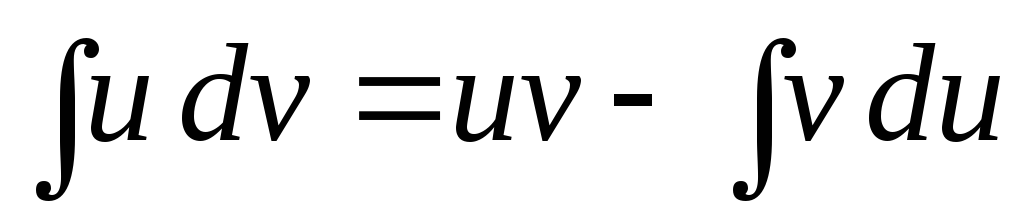 называется
называется -
К простейшим относятся дроби вида:
-
Всякую правильную рациональную дробь, знаменатель которой разложен на линейный и квадратичные множители, можно представить в виде:
-
Какой из интегралов вычисляется тригонометрической подстановкой
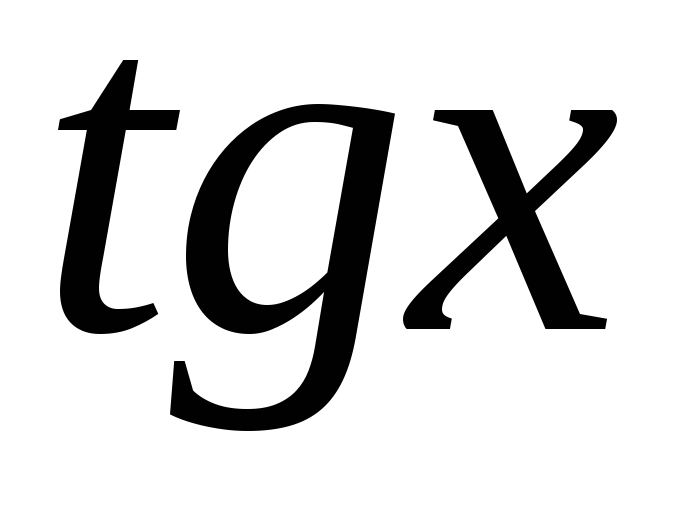 :
: -
Какой из интегралов вычисляется тригонометрической подстановкой
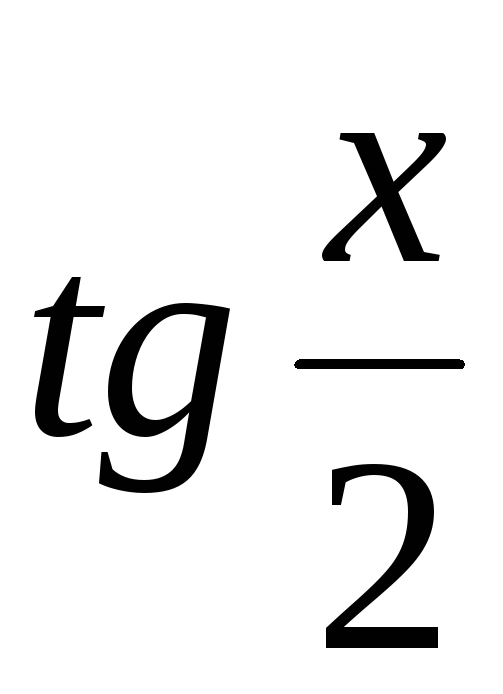 :
: -
Какой из интегралов вычисляется через наименьшее общее кратное:
-
какой из интегралов вычисляется по частям
-
вычислить пределы:
-
продифференцировать функции:
-
вычислить интегралы
