
- •(160) Телеграфные управления
- •I. Решение телеграфных уравнений для линии без потерь
- •II Решение телеграфных уравнений для линий с потерями.
- •II Учет граничных условий. Коэффициент отражения.
- •IV Режим бегущих волн.
- •V Режим стоячих волн
- •1. Линия разомкнута на конце.
- •2. Линия короткозамкнута на конце
- •3. Линия замкнута на реактивное сопротивление.
- •I. Решение телеграфных уравнений для линии без потерь 2
Длинные линии
В современной радиотехнике , кроме цепей с сосредоточенными параметрами , широкое применения находят устройства , геометрические размеры которых становятся сравнимы с длинной волны , проходящей через них , (например , различные типы линий передачи электромагнитной волны , антенные системы и др.) , поэтому напряжение и ток в таких устройствах будут функциями не только времени , но и координат , а это означает что эл.процессы в этом случае будут описываться волновыми уравнениями . совершенно очевидно , что устройства и цепи в этом случае будут характеризоваться погонными параметрами , поскольку самипараметры будут распределёнными.
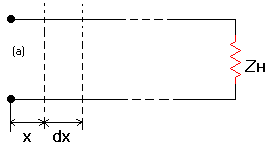 Например , два параллельных провода
рис96 можно охарактеризовать такими
погонными параметрами :
Например , два параллельных провода
рис96 можно охарактеризовать такими
погонными параметрами :
Такая цепь называется длинной линией
-
![]() -погонная
индуктивность
-погонная
индуктивность
![]() -погонная ёмкость
-погонная ёмкость
![]() -погонное сопротивление потерь
-погонное сопротивление потерь
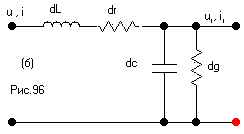
Рис.96
![]() -погонное
проводимость утечки
-погонное
проводимость утечки
т.е погонные параметры характеризуют единицу длины цепи с распределёнными параметрами .
Представление единицы длины цепи с распределёнными параметрами (рис 96а) эквивалентной схемой (рис 96 б) позволяет применить и в этом случае все законы , справедливые для цепей с сосредоточенными параметрами .
Эквивалентная схема линии конечной длины должна ,evidancetocontinueбесконечное число аналогичных звеньев , соединённых цепочечно .
Если величины
![]() не меняются по длине линии её называют
однородной ; в противном
случае – неоднородной .
не меняются по длине линии её называют
однородной ; в противном
случае – неоднородной .
Итак поскольку
ток и напряжение в линии являются
функциями координаты “x”
и времени “t”, найдём эти
зависимости . Для этого рассмотрим
элемент линииdx,удалённой
от начала на расстояниех (см.рис.96).
Обозначим искомые величины на входе
элемента (в(.)х) черезu
иiсоответственно
. Тогда значения
![]() и
и![]() на входе элемента ( в (.) х+dx)
будут
на входе элемента ( в (.) х+dx)
будут
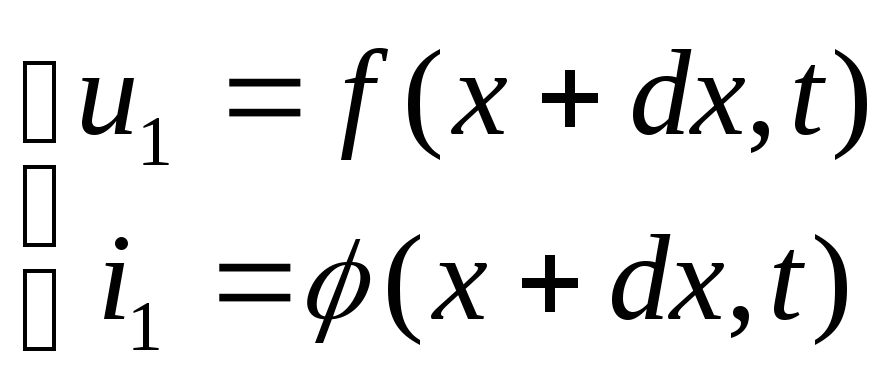
![]() (157)
(157)
Если / положим / uиi-непрерывная функцияx , тогда (157) представим так:
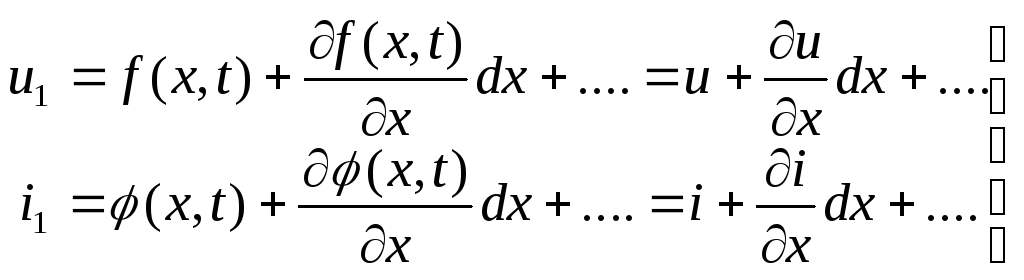 (157a)
(157a)
Ограничиваясь двумя первыми членами разложений, получим
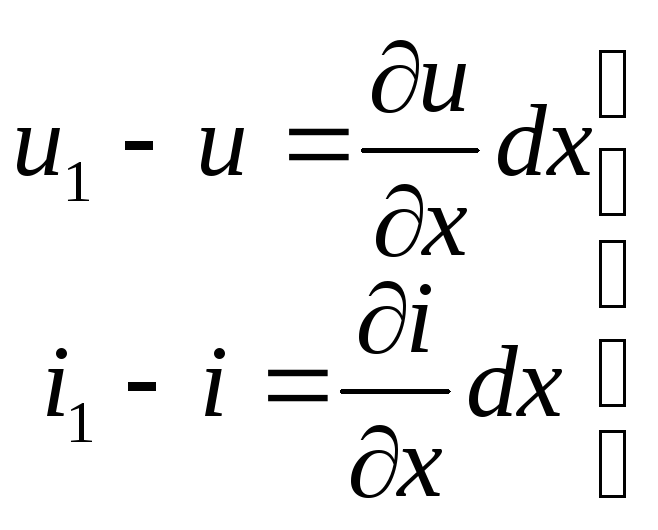 (158)
(158)
Пользуясь эквивалентной схемой элемента линии dx(рис96б) получим:
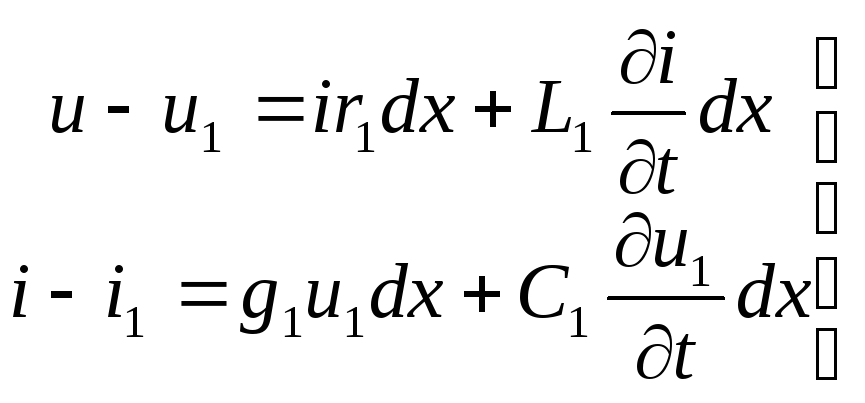 (159)
(159)
Второе уравнение из системы (159) можно переписать так:
![]() ,
поскольку точку включения параллельной
ветви можно выбирать произвольно.
,
поскольку точку включения параллельной
ветви можно выбирать произвольно.
Окончательно (158) примет вид:
(160) Телеграфные управления
I. Решение телеграфных уравнений для линии без потерь
![]()
![]() =0;
=0;
![]() =0)
=0)
Это идеализация задачи позволяет раскрыть сущность физических процессов характерных для цепей с распределёнными параметрами.
Уравнения (160) в этом случае приобретают вид:
 (161)
(161)
Продифференцируем по x иtсистему (161а). Тогда получим
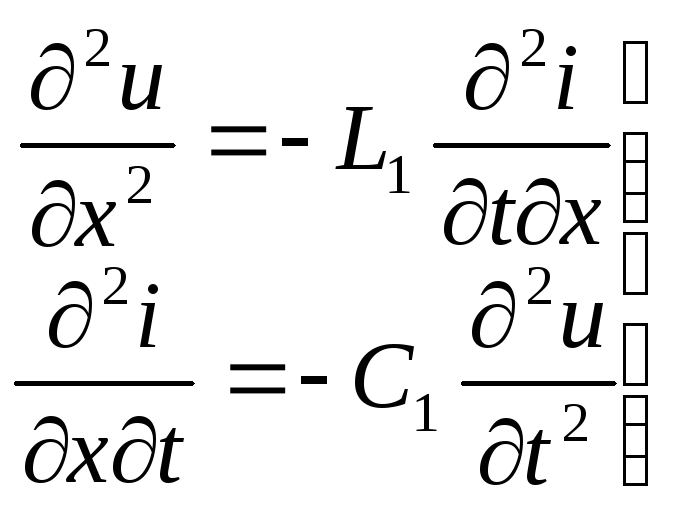 (161а)
(161а)
Отсюда следует, что функция u удовлетворяет волновому уравнению:
Аналогично для тока
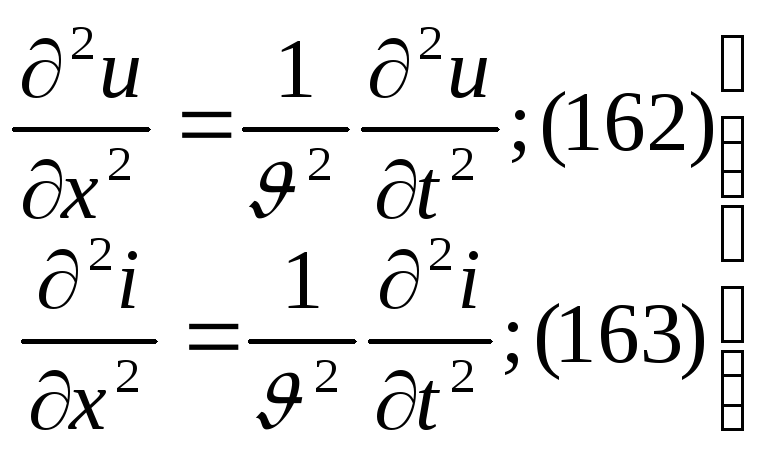 где
где![]() ;
;
Общее решение (162) может быть представлено в виде:
![]() (164)
(164)
причём функции
![]() и
и![]() конкретным условием задачи.
конкретным условием задачи.
Выясним смысл
![]() (
) и
(
) и![]() ( ) из (164) .Рассмотрим вначале функцию
( ) из (164) .Рассмотрим вначале функцию![]() .
Её значения в один и тот же момент времени
зависит отx , но
можно подобрать да момента времени
.
Её значения в один и тот же момент времени
зависит отx , но
можно подобрать да момента времени![]() и
и![]() для координат
для координат![]() и
и![]() соответственно так , что будет выполняться
равенство
соответственно так , что будет выполняться
равенство
![]()
Это справедливо , если
![]() ; пусть
; пусть![]() , тогда
, тогда
![]() и, наконец, отсюда
и, наконец, отсюда
![]() (165)
(165)
отсюда следует, что постоянное значение
функции
![]() движется по осиx со
скоростью, определяемой из (165) и зависящей
от погонных параметров линии. Это
свойство функции
движется по осиx со
скоростью, определяемой из (165) и зависящей
от погонных параметров линии. Это
свойство функции![]() даёт основание называть еёволновой
функцией иливолной (идущей в
право)
даёт основание называть еёволновой
функцией иливолной (идущей в
право)
Очевидно, что
![]() описывает волну идущуювлево (отражённую)
. Для тока в линии можно записать
аналогичное решение
описывает волну идущуювлево (отражённую)
. Для тока в линии можно записать
аналогичное решение
![]() (166)
(166)
Чтобы установить связь между напряжением и током в линии, подставим эти решения в систему (161) , например в первое уравнение:
![]()
Это равенство выполняется при любых tиx ,если
![]()
![]()
![]()
![]() Отсюда
следует, что
Отсюда
следует, что
![]()
![]()
Эти соотношения можно привести к виду:
![]() , где
, где![]() ;
(167)
;
(167)
Величина
![]() называется волновым сопротивлением
линии.
называется волновым сопротивлением
линии.
Оно в данном случае чисто активно.
Рассмотрим прямую волну. Если напряжение
в
![]() x=0 равно
x=0 равно![]() t, то напряжение и ток в
t, то напряжение и ток в![]() x
равны:
x
равны:
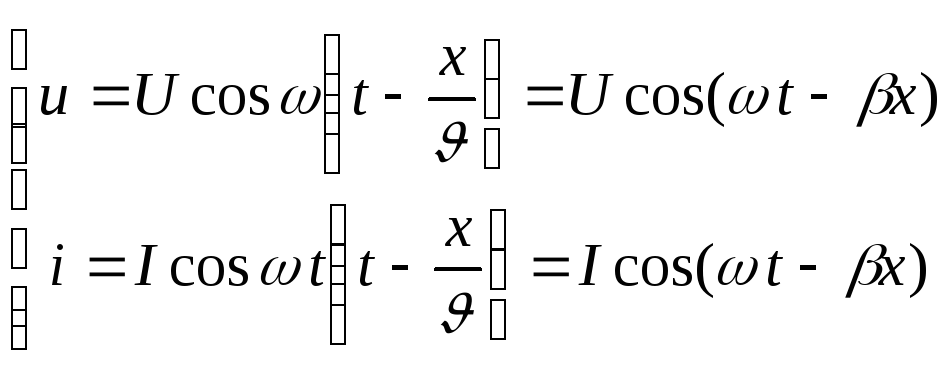
где U-амплитуда напряжения переменной волны
![]() -амплитуда
тока переменной волны
-амплитуда
тока переменной волны
![]() - волновое число.
- волновое число.
Отсюда видно, что текущие фазы (ωt-βx)
напряжения и тока приt=Constзависят отxи характеризуется
величиной β для данногоx,
поэтому β и называется коэффициентом
фазы или волновым числом. На длине волны
фаза, как известно, меняется на![]() ,
поэтому
,
поэтому![]() ;и
;и![]() ,
т.е.
,
т.е.
зависит от L1C1.
Отсюда видно, что волновой характер
процессов в линии будет проявляться
слабо, если ее длина много меньше длины
волны т.е. если![]() .
Следовательно линию можно считать
длинной в том случае, если ее длина по
крайней мере соизмерима с длиной волны.
Что касается расстояния между проводами,
образующими линию, то оно выбирается
много меньше длины волны.
.
Следовательно линию можно считать
длинной в том случае, если ее длина по
крайней мере соизмерима с длиной волны.
Что касается расстояния между проводами,
образующими линию, то оно выбирается
много меньше длины волны.
В теории линий величину
![]() электрической длиной.
электрической длиной.
II Решение телеграфных уравнений для линий с потерями.
Пусть ЭДС генератора синусоидальна,
т.е.
![]() и
и![]() ,
где
,
где
U(x) иI(x)-комплексные амплитуды напряжения и тока соответственно.
Подставляя это в уравнение (160) получим:
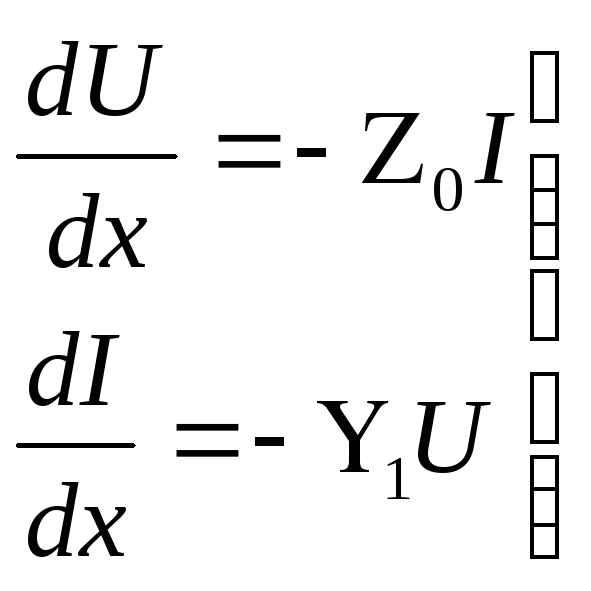 (168)
(168)![]()
Продифференцируем (168) по x:
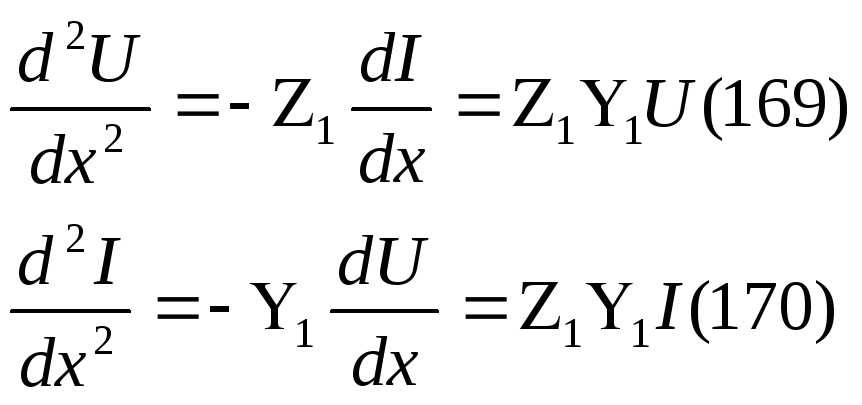
Решение (169):
![]() (171), где
(171), где![]() (172) называетсяпостоянной распространения.
(172) называетсяпостоянной распространения.
Для тока из (168) запишем
![]() или
или
![]() (173),
где
(173),
где![]() равно
равно![]() (174)
и
(174)
и
представляет собой волновое сопротивление
линии с потерями.Из формул (172) и (174)
следует, что в линии с потерями![]() и
и![]() является комплексными:
является комплексными:
![]() (175)
(175)
Выясним физический смысл
![]() ,
,![]() ,
,![]() .
Для этого рассмотрим прямую волну.
.
Для этого рассмотрим прямую волну.
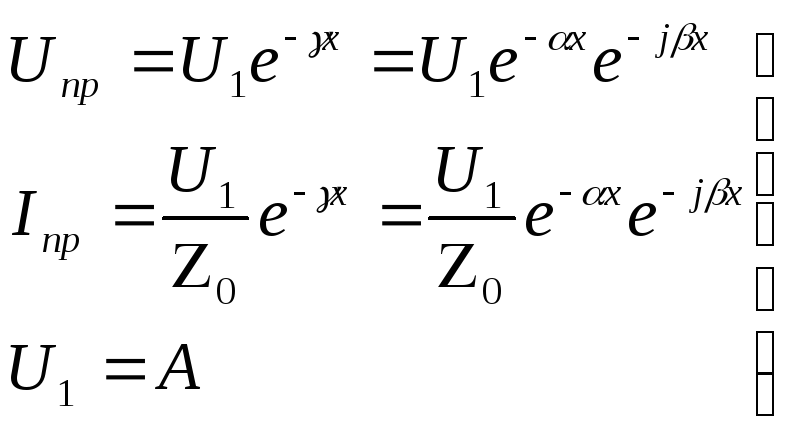 (176)
(176)
Переходя к мгновенным значениям, и полагая, что начальная фаза в точке x=0равна нулю, получим:
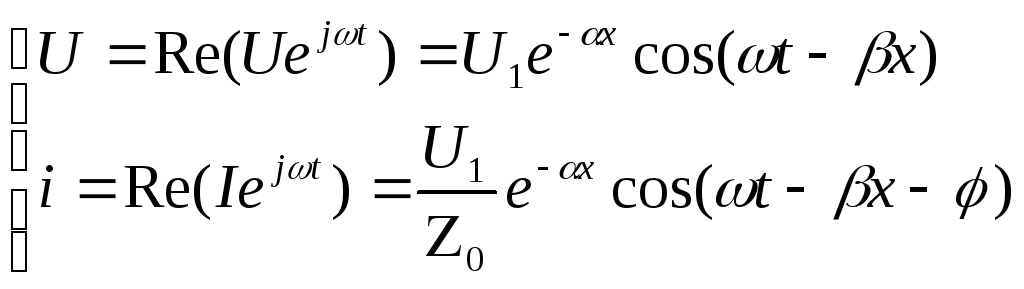 (177)
(177)
Отсюда следует, что распространение
волны вдоль линии с потерями сопровождается
экспоненциальным затуханием амплитуд.
Скорость затухания зависит от
![]() ,называемое коэффициентом затухания.
Коэффициент
,называемое коэффициентом затухания.
Коэффициент![]() -
волновое число. Угол
-
волновое число. Угол![]() характеризует сдвиг фаз между напряжением
и током прямой волны в любой точке
x.
характеризует сдвиг фаз между напряжением
и током прямой волны в любой точке
x.
