2.3. Колебательное звено.

Уравнение и передаточная функция звена:

(T₂²p²+T₁p+1)Y(p)=kX(p), W(p)=,

причем предполагается T₁<2Т₂, так что корни характеристического уравнения T₂²p²+T₁p+1=0 — комплексные.

Общепринята запись передаточной функции колебательного звена в виде:

W(p)=,

где Т=T₂, = причем 0<<1, так как T₁<2Т₂. При 1 звено становится инерционным звеном второго порядка.

Амплитудно-фазовая частотная характеристика (рис.16) звена:

W(j)=, A()=, ()=-arctg.

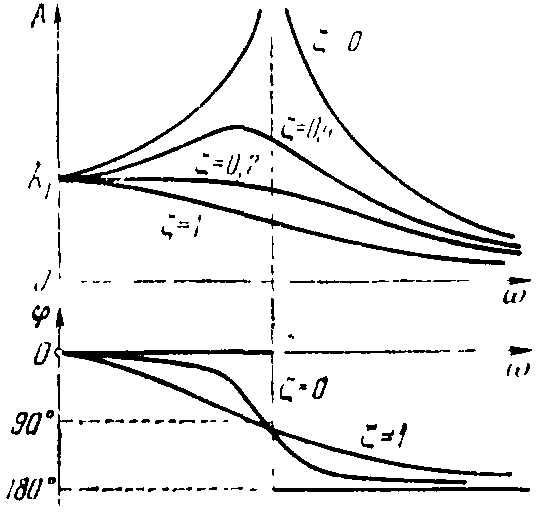
Рис.16. Частотные характеристики колебательного звена.

Амплитудная характеристика уменьшается с увеличением , т.е. А()k, если 1>>0,707. При <0,707 появляется максимум на характеристике А(), который уходит в бесконечность при 0. Поэтому величина = называется параметром затухания. Отсюда видна роль постоянных времени Т₁ и Т₂ в уравнении звена: постоянная Т₂ увеличивает колебания, а T₁ — демпфирует их.

Логарифмическая амплитудная частотная характеристика звена

L()=20lgk-20lg.

При значениях 0,5<<1 характеристика близка к ломаной (рис.17).

Рис.17. Логарифмические частотные характеристики колебательного звена.

Если же <0,5, то получается заметный максимум (рис.17). Максимум характеризуется превышением H_m

H_m=20lg

на частоте

_m=.

В упрощенных расчетах достаточно находить H_m приближенно (см. рис.17):

H_m20lg при =.

Переходная функция колебательного звена изображена на рис.18.

Рис.18. Переходная функция колебательного звена.

Она имеет вид:

h(t)=.

При =1 колебания вырождаются в апериодический процесс.

При =0 колебания становятся незатухающими (периодическими), и в этом случае колебательное звено носит название консервативного звена.

Примеры колебательных звеньев изображены на рис.19.

Рис.19. Примеры колебательных звеньев

2.4. Идеальное интегрирующее звено.

Уравнение и передаточная функция:

y(t)=k или Y(р)=X(p), W(p)=.

Амплитудно-фазовая частотная характеристика звена (рис.20):

W(j)=-j, A()=, ()=-90°.

Рис.20. Частотные характеристики интегрирующего звена.

Логарифмическая амплитудная частотная характеристика показана на рис.21 вместе с фазовой частотной характеристикой:

L()=20lgk-20lg

Рис.21. Логарифмические частотные характеристики интегрирующего звена.

Переходная функция (рис.22) имеет вид: h(t)=kt, t>0.

Рис.22. Переходная функция интегрирующего звена.

Пример идеального интегрирующего звена изображен на рис.23.

Рис.23. Пример идеального интегрирующего звена.

2.5. Идеальное дифференцирующее звено.

Уравнение и передаточная функция звена:

y(t)=k, Y(p)=kpX(p), W(p)=kp.

Амплитудно-фазовая частотная характеристика (рис.24) звена:

W(j)=jk, A()=k, ()=+90°.

Рис.24. Частотные характеристики идеального дифференцирующего звена.

В реальных системах такой вид характеристик звена возможен лишь в ограниченной полосе частот.

Логарифмические частотные характеристики (рис.25):

L()=20lgk+20lg, ()=+90°.

Рис.25. Логарифмические частотные характеристики идеального дифференцирующего звена.

Переходная функция имеет вид: h(t)=k(t), t>0.

Примерами такого типа звена являются (рис.26) тахогенератор и RC-цепочка с усилителем.

Рис.26. Примеры дифференцирующих звеньев.