Раздел II. Аналитическая планиметрия Лекция 1. Аффинные системы координат на плоскости. Метод координат §1. Аффинная система координат на плоскости

О п р е д е л е н и е. Аффинной системой координат на плоскости (аффинным репером) называется точка и два неколлинеарных вектора: .

Прямые и, определяемые точкойи векторамии, называются соответственно осью абсцисс и осью ординат.

Частным случаем аффинной системы координат является прямоугольная система координат , определяемая точкойи ортогональными ортами.

О п р е д е л е н и е. Вектор называетсярадиус-вектором точки .

О п р е д е л е н и е. Координатами точки называются координаты её радиус-вектора: .

У п р а ж н е н и е. Построить точку по координатам в заданном аффинном репере.

У п р а ж н е н и е. Найти координаты вершин правильного шестиугольника с центромотносительно аффинной системы координат.

Отметим простейшие задачи, решаемые с помощью координат

1. Определение координат вектора по координатам начала и конца относительно аффинной системы координат .

.

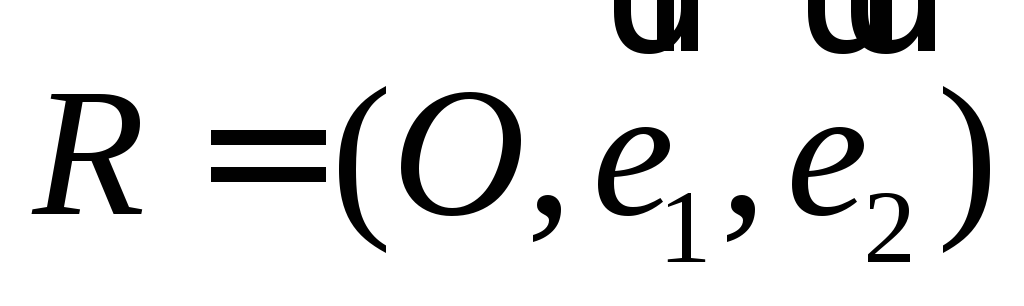2. Определение координат точки по заданному простому отношению трех точек прямой и координатам двух из них относительно аффинной системы координат .

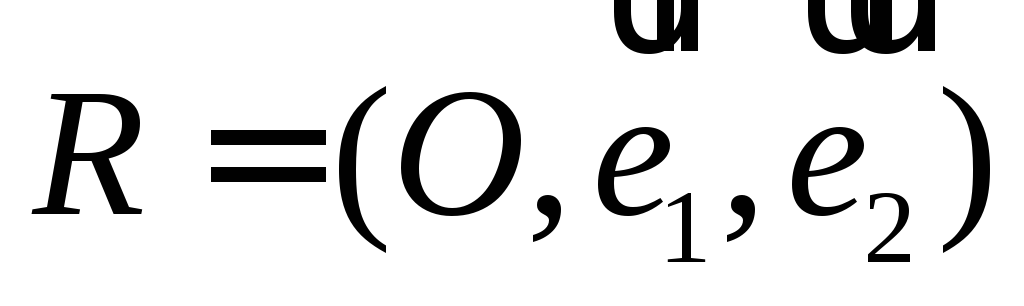О п р е д е л е н и е. Простым отношением трех точек прямой, заданных в указанном порядке, называется число, такое, что(обознач.).

У п р а ж н е н и е. На прямой выбраны точки так, что. Определить.

Пусть и, то есть. Переходя к коррдинатам векторов, получим:. Отсюда получаем возможность выразить координаты точки:.

В частности, если середина, тои получаем– координаты середины отрезка равны полусуммам соответствующих координат концов отрезка.

3. Вычисление расстояния между точками по координатам относительно прямоугольной системы координат .

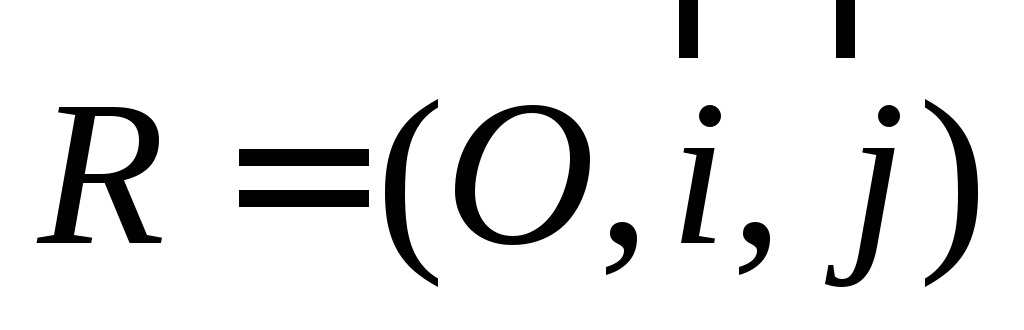Расстояние между точками иможно найти как длину вектора. Поскольку базис ортонормированный, то получаем

–расстояние между точками равно корню квадратному из суммы квадратов разностей соответствующих координат точек.

§2. Формулы преобразования координат

При изменении системы координат будут меняться координаты точек. Как будет происходить это изменение?

Перейдем от репера к реперу, где известны координаты точкиотносительно репераи координаты векторовив базисе:,,

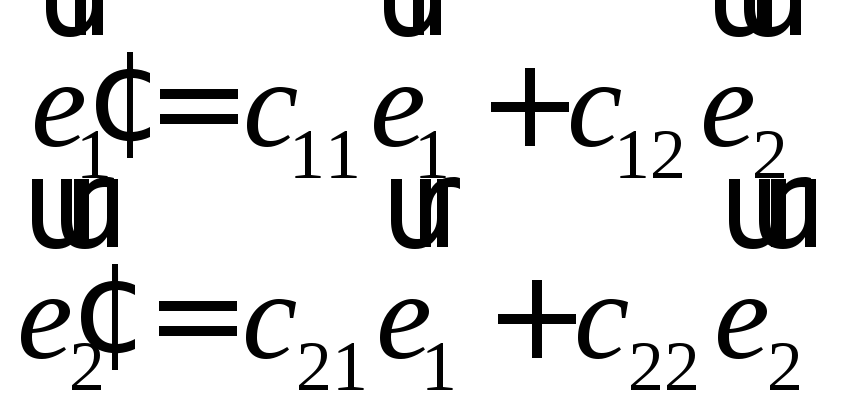здесь 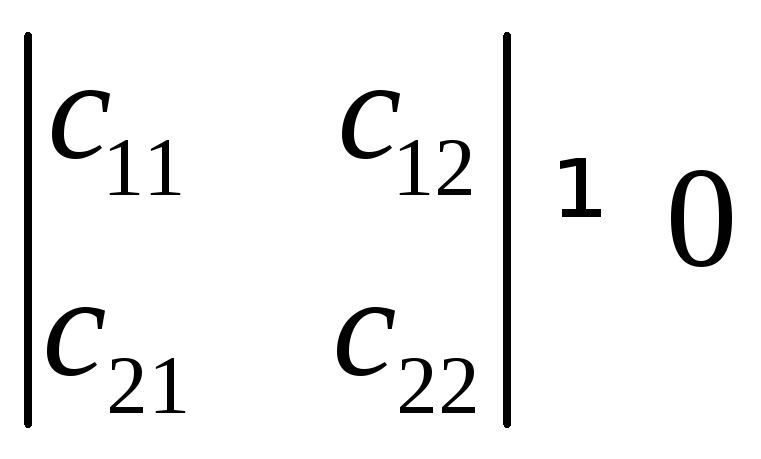, так как векторыиобразуют базис.

Для произвольной точки плоскости имеем координатыотносительно репера– старые координаты, и координатыотносительно репера- новые координаты. Выразим старые координаты точки через её новые координаты. Имеем

. (1)

(– радиус вектор точкив репере).

(– радиус-вектор точкив репере).

Учитывая это и разложение векторов ипо векторам базиса, из (1) получимформулы преобразования координат при замене аффинного репера:

(*).

Если при замене репера меняется только начало системы координат, то есть, тои формулы (*) принимают вид:

–формулы преобразования координат при переносе начала системы координат.

Произвольную замену репера можно осуществлять в два этапа: перенос начала системы координат и замена координатных векторов.

Особо рассмотрим преобразование прямоугольной системы координат.

Пусть реперы иориентированы одинаково. Отложив векторыиот точки, найдем координаты этих векторов в базисе.

Имеем ,.

Формулы (*) примут вид

(**).

Из них, в частности, получим формулы преобразования координат при повороте осей прямоугольной системы координат на угол :

Проведя аналогичные рассуждения в случае противоположно ориентированных реперов и, получим формулы

(***).

Формулы (**) и (***) можно записать в общем виде

, где .