V. Итоги урока.

В о п р о с ы у ч а щ и м с я:

– Назовите основные этапы решения текстовой задачи алгебраическим методом.

– Какие способы схематичной записи условия задачи вы знаете?

– В чём особенности решения задач на концентрацию?

– В чём особенности решения задач на движение, если в тексте идёт речь о движении по реке?

Домашнее задание: № 626, № 628, № 627 (дорешать уравнение), № 629 (дорешать уравнение).

У р о к 3 (60) Решение задач на совместную работу и задач повышенной сложности

Цели: продолжить формирование умения решать текстовые задачи с помощью дробных рациональных уравнений; формировать умение решать задачи на совместную работу и задачи повышенной сложности.

Ход урока

I. Организационный момент.

II. Самостоятельная работа.

В а р и а н т 1

Теплоход, собственная скорость которого 18 км/ч, прошёл 50 км по течению реки и 8 км против течения, затратив на весь путь 3 ч. Какова скорость течения реки?

В а р и а н т 2

Катер прошёл 40 км по течению реки и 6 км против течения, затратив на весь путь 3 ч. Какова собственная скорость катера, если скорость течения 2 км/ч?

III. Формирование умений и навыков.

Все задачи, решаемые на этом уроке, можно разбить на т р и группы:

1) Задачи на конкретную работу.

2) Задачи на абстрактную работу.

3) Задачи повышенной трудности.

В задачах на работу фигурируют величины: производительность (р), время (t) и работа (А), связанные формулой A = p · t. Причём в задачах на конкретную работу мы за А принимаем конкретное число (количество выточенных деталей, количество напечатанных страниц и т. п.), а в задачах на абстрактную работу принимаем значение А, равное 1 (заполнен водой бассейн, вспахано поле и т. д.).

Необходимо разъяснить учащимся, что это не искусственный приём. Каждый участник выполняет часть работы: и т. д.

1. Две мастерские должны были пошить по 96 курток. Первая мастерская шила в день на 4 куртки больше, чем вторая, и потому выполнила заказ на 2 дня раньше. Сколько курток шила в день каждая мастерская?

Р е ш е н и е

А н а л и з:

	р, шт./день	t, день	А, шт.
1-я мастерская	х + 4		96
2-я мастерская	х		96

По условию большена 2 дня.

Пусть 2-я мастерская шьёт в день х курток, тогда 1-я мастерская в день шьёт (х + 4) куртки. Первая мастерская выполнит заказ за дня, а вторая – задня. Зная, что первая мастерская шила на 2 дня меньше, составим уравнение:

–= 2; ОДЗ: х ≠ 0, х ≠ –4.

96(х + 4) – 96х = 2х(х + 4);

384 – 2х² – 8х = 0;

х² + 4х – 192 = 0;

D₁ = 2² + 192 = 196, D₁ > 0, 2 корня.

x₁ = –2 + = –2 + 14 = 12;

x₂ = –2 – = –2 – 14 = –16 – не удовлетворяет условию задачи. Значит, вторая мастерская в день шила 12 курток, а первая 16.

О т в е т: 16 курток, 12 курток.

2. № 632.

Р е ш е н и е

А н а л и з:

	р	t	А
I, II	р1+р2	6	1
I	х		1
II	–х	1 :	1

По условию задачи больше 1 :на 5 часов.

Пусть х – производительность первого крана, тогда – производительность второго крана. На разгрузку баржи первый кран затратилчасов, второй 1 :. Зная, что первому крану потребовалось на 5 часов больше, составим уравнение:

–= 5;

= 5;

= 5; ОДЗ: х ≠ 0, х ≠ .

1 – 6х – 6х = 5х(1 – 6х);

1 – 12х – 5х + 30х² = 0;

30х² – 17х + 1 = 0;

D = (–17)² – 4 · 30 = 289 – 120 = 169, D > 0, 2 корня.

x₁ = ;

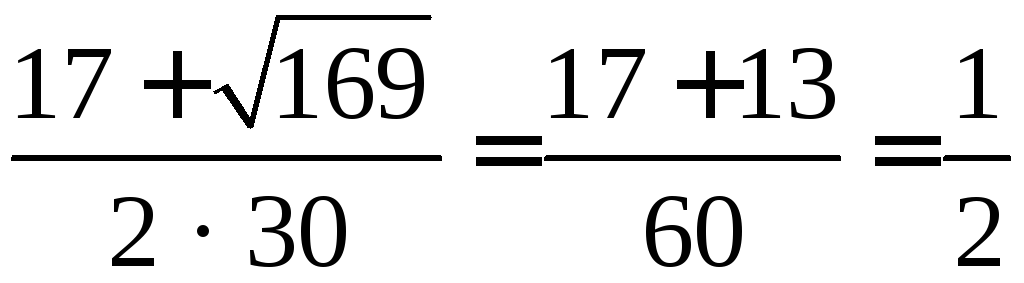x₂ = .

x₁ = не удовлетворяет условию задачи, так как первый кран в этом случае разгрузит баржу за 2 часа.

Имеем: первый кран разгрузит баржу за 15 часов, а второй – за 10 часов.

О т в е т: 15 часов, 10 часов.

3. Слесарь может выполнить заказ за то же время, что и два ученика, работая вместе. За сколько часов может выполнить заказ слесарь и каждый из учеников, если слесарь может выполнить его на 2 часа скорее, чем один первый ученик, и на 8 часов скорее, чем один второй?

4. Если останется на уроке время и для сильных в учебе учеников, можно предложить для решения задачу повышенной трудности.

№ 634*.

Р е ш е н и е

А н а л и з:

V1=х(км/ч)

П С

V2=х+ 5 (км/ч)

Пусть х км/ч – скорость велосипедиста от посёлка до станции. Обозначим этот путь за 1. Тогда от посёлка до станции велосипедист ехал , а от станции до посёлкачасов, значит, всего в пути он былчасов, а весь путь составил 2. Зная, что средняя скорость на всем пути следования составляла 12 км/ч, получим уравнение:

12 · 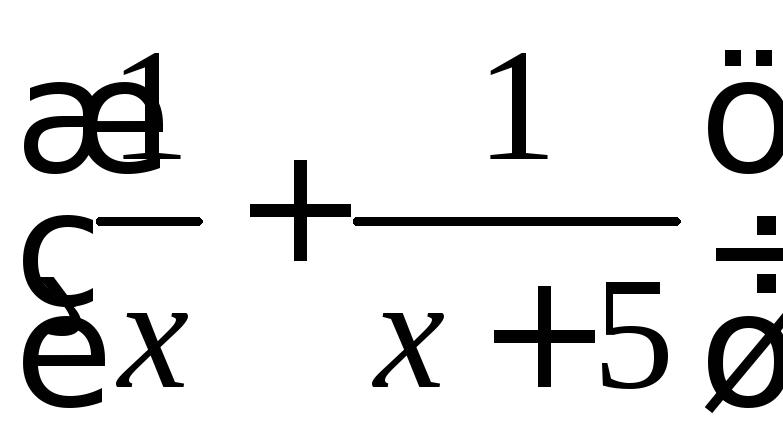= 2;

= 1; ОДЗ: х ≠ 0; х ≠ –5.

6(х + 5) + 6х = х(х + 5);

6х + 30 + 6х – х² – 5х = 0;

–х² + 7х + 30 = 0;

х² – 7х – 30 = 0.

По теореме, обратно теореме Виета, х₁ = 10; х₂ = –3 – не удовлетворяет условию задачи.

О т в е т: 10 км.