Точилкина Ольга / LABA3

На практике управления и прогнозирования деятельности крупных систем особое место занимает задача определения весов частных критериев в критерии оптимальности социально-экономического объекта. Рассмотрим эту проблему в предположении о линейном характере зависимостей в модели планирования производственно-хозяйственной деятельности объекта.

Итак, пусть на практике в неявной форме фирмой решается следующая задача среднесрочного планирования:

AX = B (1)

X  0,

где Х – вектор плана на следующий период, В – вектор ограничений ресурсов, А – матрица затрат ресурсов. Здесь, в отличие от обычной задачи линейного программирования, вектор целевой функции w задается не в явном виде, а как линейная комбинация векторов с_k, каждый из которых задает форму целевой функции в зависимости от того, какую цель преследует предприятие. Например, если предприятию необходимо максимизировать выручку, вектор будет одного вида, а при необходимости максимизировать прибыль – другого (поскольку в целевую функцию добавятся со знаком «минус» издержки). Такой вектор обзовем частным критерием оптимальности. Когда руководство предприятия решает, какая цель для него в данный момент важнее, оно ранжирует частные критерии по степени важности, и в конечном итоге целевая функция приобретает вид, не свойственный ни одному из частных критериев по отдельности. Это достигается путем умножения частных критериев оптимальности на некий вес, выражающий степень его важности количественно, и последующего суммирования получившихся «взвешенных» критериев. Эту сумму обзовем критерием оптимальности (во избежание путаницы, хотя, по сути дела, она представляет собой целевую функцию). Веса образуют вектор . Принято представлять его в нормированном виде, т.е. .

Для восстановления весов _k можно воспользоваться условиями Куна-Таккера. Это необходимые и достаточные условия достижения максимума целевой функции системы 1 в точке X₀. Для задачи эти условия имеют вид:

, где

I(X⁰) - множество активных ограничений «по строкам», т.е. тех ограничений, которые обращаются в равенство при подстановке в них конкретных значений оптимального плана. Это значит, что при данном оптимальном плане i-й ресурс полностью используется, следовательно, он является «узким местом» в производстве, и при изменении количества этого ресурса оптимальное значение целевой функции обязательно изменится (в то время как изменение количества ресурса из «неактивного» ограничения не влечет за собой изменение оптимального значения целевой функции). Эти словеса можно пояснить графически (см. рис. 1)

J(X⁰) - множество активных ограничений «по столбцам», т.е. это номера нулевых элементов вектора оптимального плана. Заметим, что если j-й элемент вектора оптимального плана равен нулю, то это значит, что данный продукт предприятие в данном периоде не выпускает, следовательно, ресурсы на его производство не тратит.

- градиент функции точке X⁰, то есть по сути дела столбец коэффициентов целевой функции.

y_i - множитель Лагранжа или двойственная оценка соответствующего ограничения. Двойственная оценка показывает, на сколько единиц изменится целевая функция при изменении правой части i-го ограничения на единицу. Двойственная оценка может принимать как положительные, так и отрицательные значения (она не будет обнуляться в силу того, что в данной системе используются только активные ограничения). В первом случае при увеличении i–го ресурса целевая функция возрастает, во втором случае уменьшается. Оба случая проиллюстрированы на рис. 2 (а – двойственная оценка положительна, б – двойственная оценка отрицательна). С экономической точки зрения первый случай может быть пояснен примером. Пусть целевая функция задает выручку при условии выпуска предприятием 4 видов продукции. Матрица затрат трактуется традиционно. Тогда при увеличении запаса ресурса из множества активных ограничений целевая функция возрастет. Пусть теперь целевая функция – не выручка, а прибыль. Пусть имеется активное ограничение, описывающее каким-то образом (неважно, каким) максимальную численность рабочих на предприятии. При увеличении этой максимальной численности увеличится общий фонд заработной платы, следовательно, возрастут издержки. Значит, «минусовая» часть целевой функции возрастет, а само ее значение уменьшится (разумеется, при прочих равных условиях), что соответствует отрицательной двойственной оценке.

v_j - неотрицательное число, связанное с соответствующими активными ограничениями «по столбцам» подсистемы. Эти числа вводятся для того чтобы превратить неравенство в равенство (разумеется, при условии, что IJ. В противном случае данное неравенство уже является равенством в силу активности ограничения). Неравенство представляет собой не что иное, как j-е ограничение двойственной задачи. Превратив все неравенства в равенства, мы сможем решить полученную задачу симплекс-методом, например, в ППП «BLP-88».

Таким образом, X⁰ является оптимальным планом системы 1 в том и только в том случае, если удастся подобрать произвольные числа y_i, и неотрицательные v_j, такие, что выполняется указанное выше векторное равенство. Преобразуя его, получаем следующую систему уравнений:

(2)

Общее решение системы (2) дает множество возможных весов _k и если оно состоит более чем из одного элемента, то все допустимые наборы весов  входящие в него, могут использоваться для прогнозирования поведения социально-экономического объекта. Если же множество  пусто, это значит, что использованы не все частные критерии или сама схема неправильно описывает систему предпочтений лица принимающего решения от имени объекта.

Этап 1.

На основе исходной информации об условиях функционирования объекта в течение одного периода времени осуществляем математическую формализацию задачи восстановления критерия оптимальности.

Исходные данные. 3-й период.

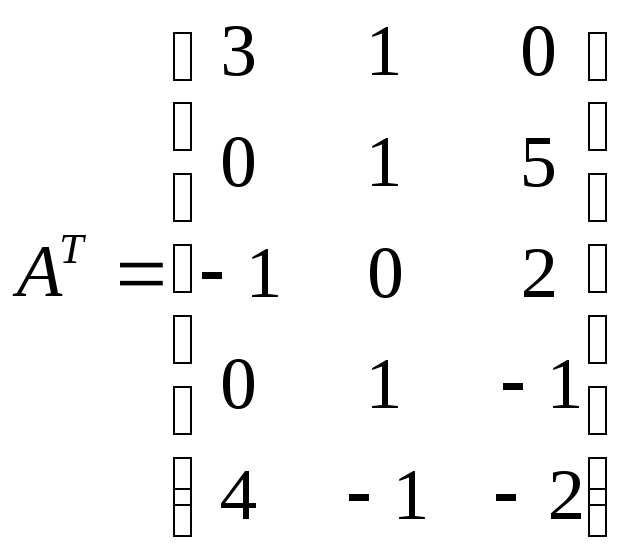
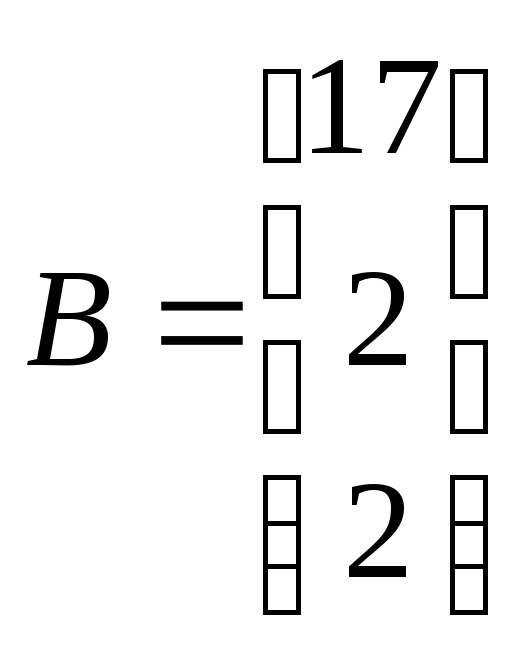
Рассматриваются 2 частных линейных критерия оптимальности, которым соответствуют вектора коэффициентов:

В этих условиях был выбран план:

Множество активных ограничений «по строкам»: I={1,2}

Множество активных ограничений «по столбцам»: J={3,4}

Запишем систему (2):

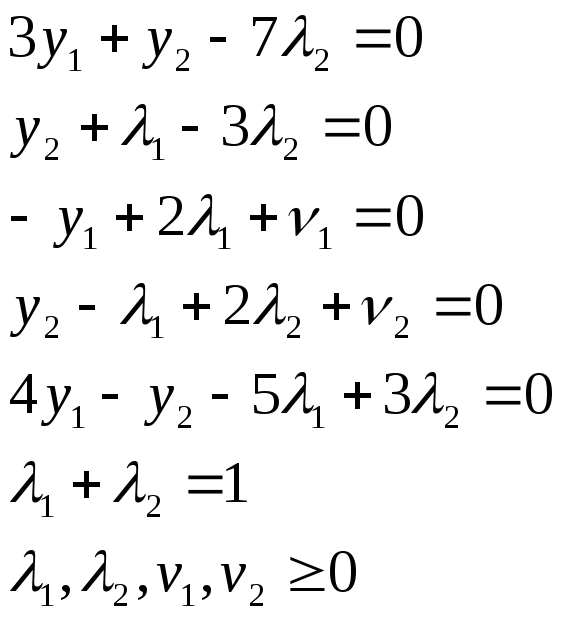
Для того, чтобы найти решение этой системы с помощью пакета BLP преобразуем эту систему следующим образом. Т.к. у может принимать любой знак (обоснование сего факта см. выше), а ВLP предполагает, что на все переменные накладывается ограничение неотрицательности, то будем задавать у с помощью следующего выражения: . Кроме того, введем дополнительные фиктивные переменные q_1..5, которые неотрицательны. Задавшись целью минимизировать их сумму (точнее, обратить ее в 0) и прибавив q_i к левой части i–го ограничения, получим стандартную задачу линейного программирования. От таких преобразований решение задачи ЛП будет таким же, как и решение системы уравнений (т.к. q_i = 0 при любых i), поэтому наши действия вполне правомерны.

Решим эту систему с помощью пакета решения задач линейного программирования BLP. Результаты в Приложении №1.

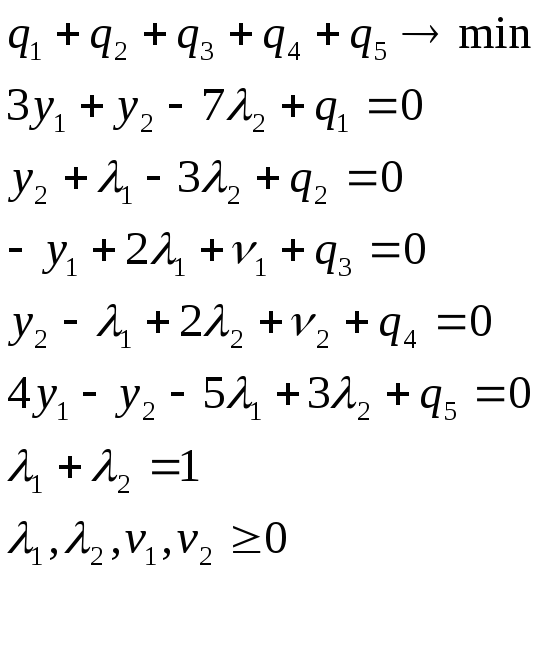
Вектор  имеет вид :

Система имеет единственное решение (т.к. все оценочные коэффициенты при небазисных переменных строго положительные).

Этап 2.

Восстановим критерий оптимальности фирмы, если существует ряд наблюдений за несколько периодов времени. Для этого решим систему (2) совместно для каждого периода:

Исходные данные. 1-й период.

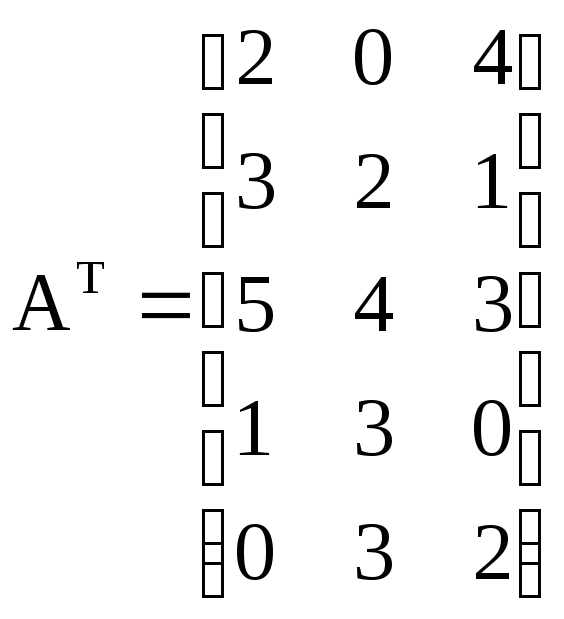
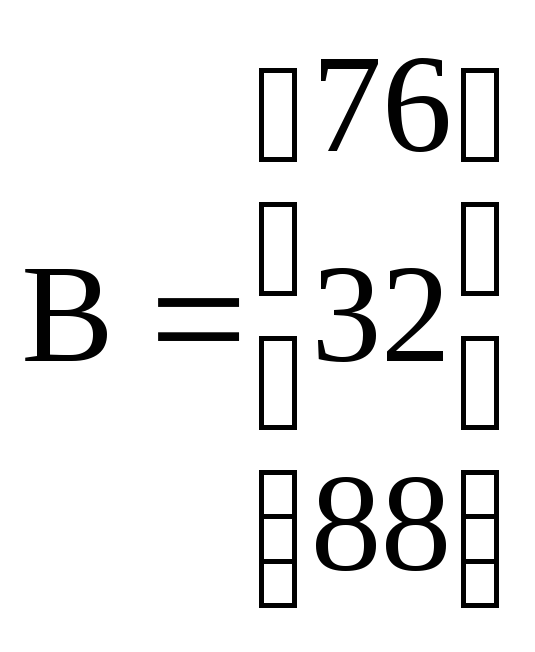
Рассматриваются 2 частных линейных критерия оптимальности, которым соответствуют вектора коэффициентов:

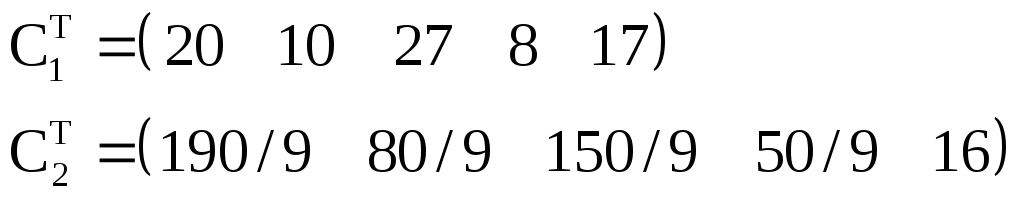
В этих условиях был выбран план:

Множество активных ограничений : I={2,3}

Множество активных ограничений : J={2,4,5}

Запишем систему (2):

Исходные данные. 2-й период.

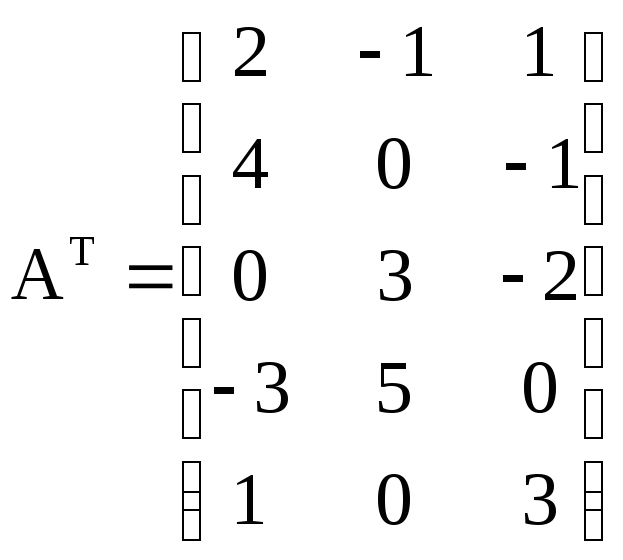
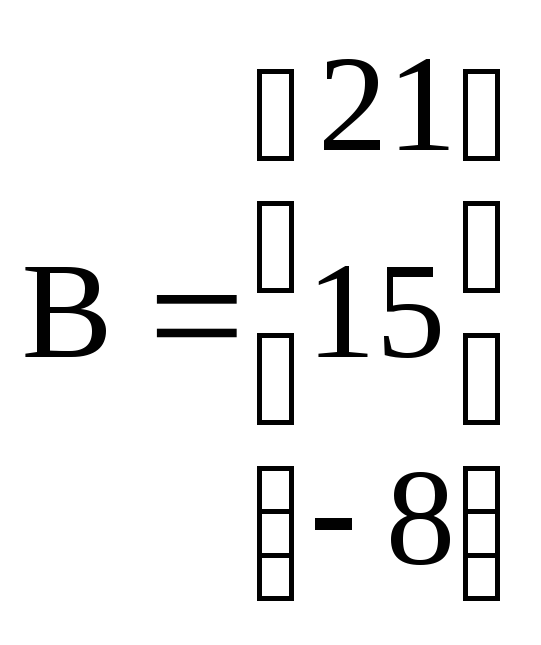
Рассматриваются 2 частных линейных критерия оптимальности, которым соответствуют вектора коэффициентов:

В этих условиях был выбран план:

Множество активных ограничений : I={1,3}

Множество активных ограничений : J={1,4}

Запишем систему (2):

Система для 3-его периода была составлена выше.

Для составления совместной системы воспользуемся следующей предпосылкой: будем минимизировать расстояние от оптимального решения всей системы до оптимальных решений каждой подсистемы в отдельности. Это расстояние можно измерять как сумму модулей отклонений по весам: .

Тогда вектор как оптимальное решение всей системы определяется из решения следующей задачи:

Тогда искомая система примет следующий вид:

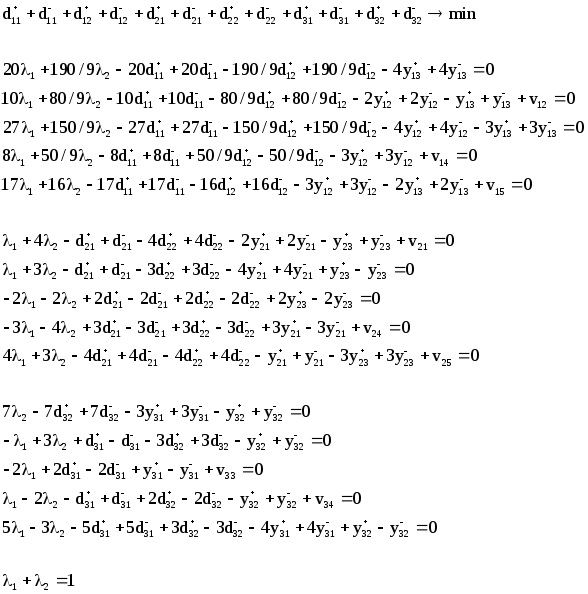
Решая данную систему в пакете BLP получаем единственное оптимальное решение (см. Приложение №2).

Этап 3.

Используя выявленную на этапе 2 структуру предпочтений производственно-хозяйственного объекта, и предполагая условия его функционирования в течение последующего, 4-го периода времени аналогичным 3-му, осуществим прогноз деятельности фирмы. Найдем общее решение системы (1).

Исходные данные. 4-й период.

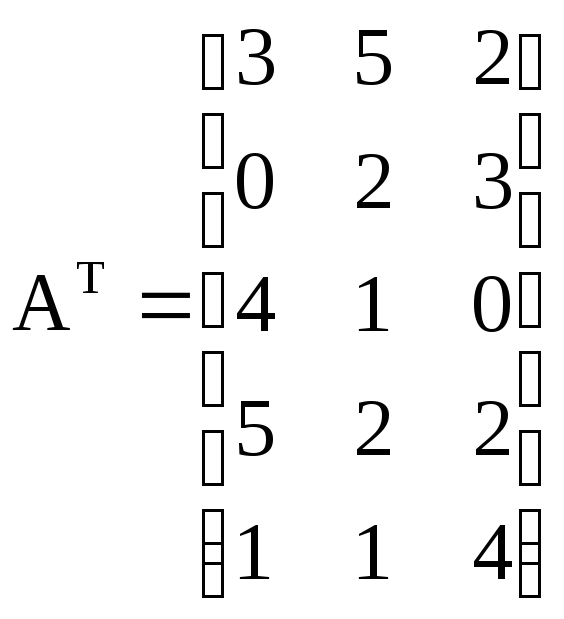
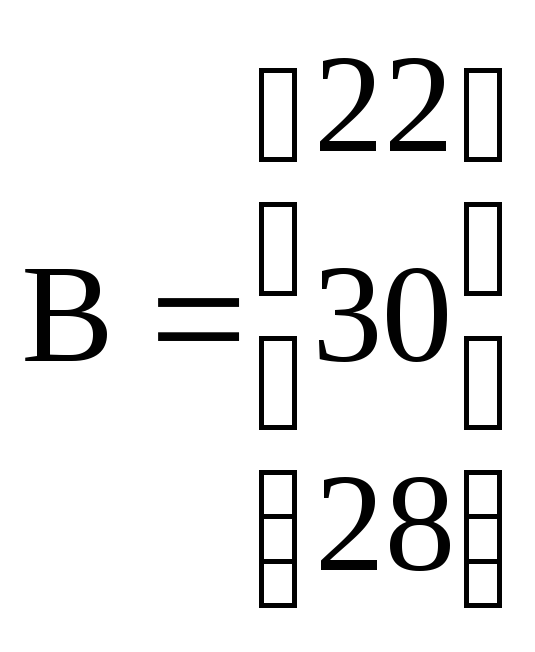
Рассматриваются 2 частных линейных критерия оптимальности, которым соответствуют вектора коэффициентов:

Запись системы (1) :

Решим эту задачу с помощью BLP. Результаты см. в Приложении №3

Найденный оптимальный план - единственный:

Этап 4.

Проверим, насколько устойчиво определены веса частных критериев. Для этого определим веса по данным 4-го периода, а затем сравним результаты с вектором , полученным на 2 этапе.

Исходные данные. 4-й период.

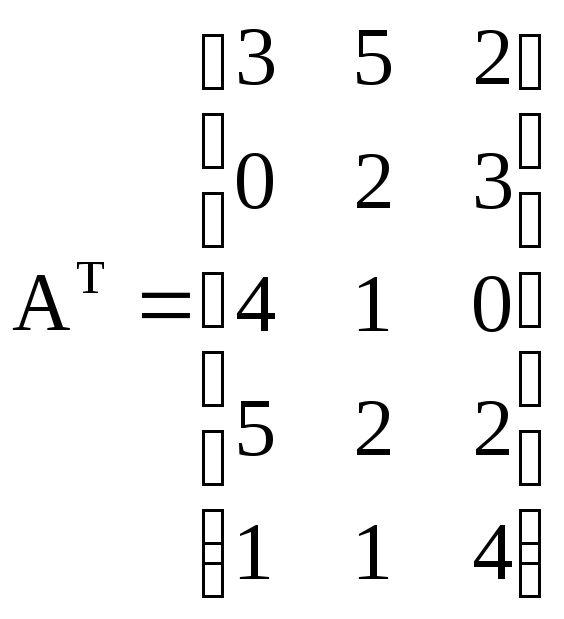
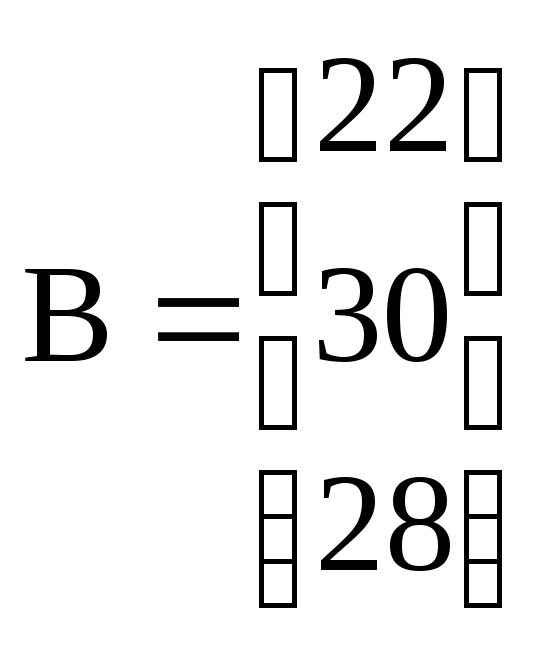
Рассматриваются 2 частных линейных критерия оптимальности, которым соответствуют вектора коэффициентов:

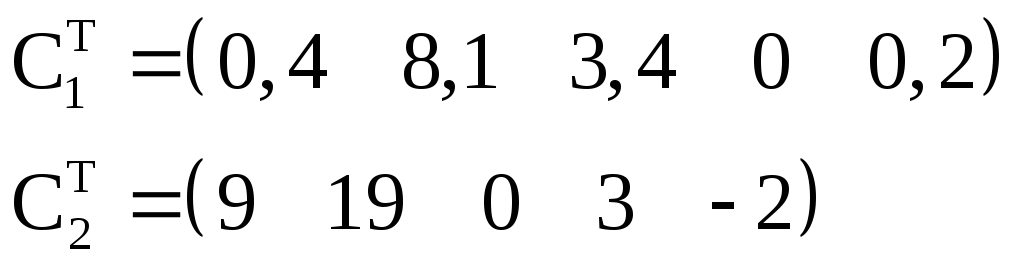
В этих условиях был выбран план:

Множество активных ограничений : I={}

Множество активных ограничений : J={2}

Т.к. I не удается определить в явном виде, для его нахождения воспользуемся следующим условием: необходимо найти грани многогранника ограничений, которые удалены от точки х₀ на расстояние меньшее =0,5. Это расстояние можно найти по формуле:

.

В результате расчетов получаем:

Следовательно, 3-я и 2-я грани многогранника ограничений удалены от точки x₀ на расстояние меньшее =0,5. Тогда выбираем их в качестве активных ограничений, т.е. множество активных ограничений следующее: I={2,3}

Запишем систему (2):

Решим эту задачу с помощью BLP. Результаты см. в Приложении №4