1. Проверка ряда на стационарность

REM: см. Приложение1

1. Определение тренда и проверка гипотезы о правильности выбора тренда

В результате построения линейной трендовой модели получили следующие результаты расчетов.

Вид модели	R2,%	S	F
4,55+2,02*t	99,48	1,31	5321

Значимость параметров модели

Параметр	S	tрасч	t(0,05;29)
4,55	0,5	9,3	2,05
2,02	0,03	73	2,05

Проверка гипотезы о правильности выбора вида тренда заключается в том, что отклонения от тренда будут носить случайный характер.

Критерий серий (основанный на медиане выборки)

Рассчитаем отклонения от тренда ₁,₂, … ,₃₀, отсортировав, найдем медианное значение. Рассмотрим исходный ряд отклонений и сравним полученные значения с медианным_медпо следующему правилу

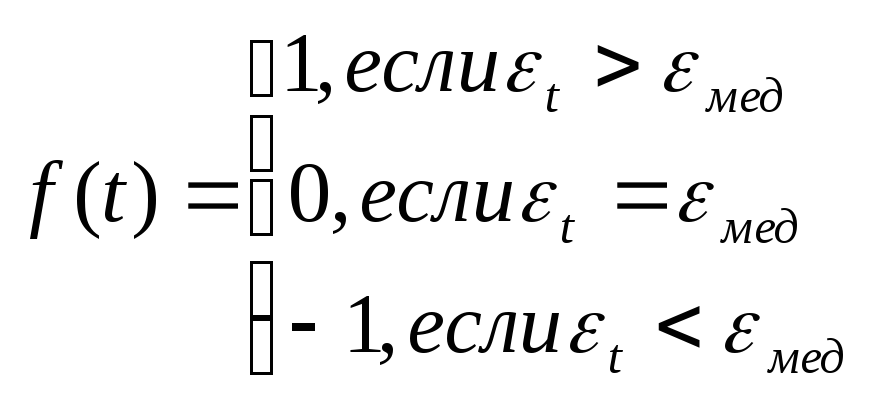
Последовательность идущих подряд 1 или –1 называется серией. Если отклонения от тренда случайные, то чередование серий должно быть также случайным. Для аналитической оценки случайности отклонений используют следующий метод: подсчитывают длину самой длинной серии К_мах(30) и общее число серий(30). Выборка признается случайной если выполняются следующие неравенства (для 5% уровня значимости):

В результате расчетов получили, что медиана _мед= 0,15,

K_max(30) = 4 < 8,175

(30) = 20 >10,223.

Таким образом, отклонение уровней временного ряда от тренда случайно, и уравнение тренда составлено правильно.

2. Проверка гипотезы о стационарности случайного компонента

Основным условием стационарности случайного процесса является зависимость автокорреляционной функции только от разности аргументов

t_i – t_j = . На практике ориентируются на   n / 4, в нашем случае  = 7.

Для проверки гипотезы о том, что значение автокорреляционной функции зависит не от выбора начала отсчета наблюдений, а только от величины сдвига , найдем для случайного компонента _t (t = 1, …, 30) значения автокорреляционной функции . Затем, исключив последнее наблюдение найдем новую автокорреляционную функцию, и так далее, исключаяk (k = 0, 1, …, K) наблюдений, получим  = 7 групп, содержащих по K + 1 коэффициентов автокорреляции, так как рассматриваемый ряд наблюдений содержит 30 значений, то возьмем К=10, большее количество брать не целесообразно, т.к. ряд не будет коротким и полученные коэффициенты не будут адекватными реальной ситуации.

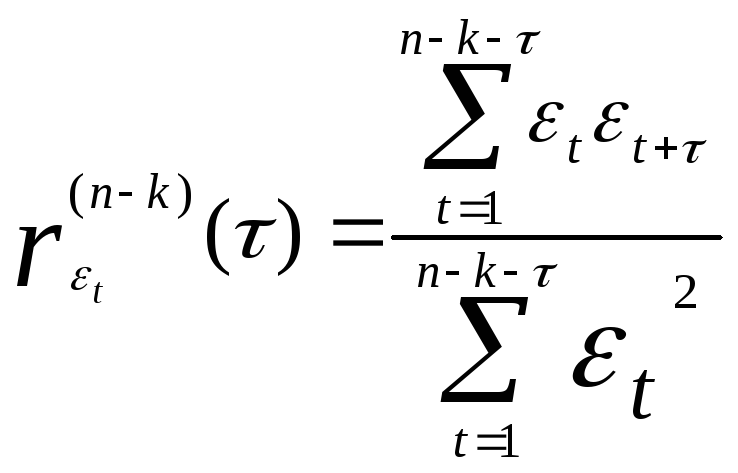
Для стационарного в широком смысле случайного процесса коэффициенты автокорреляции, входящие в одну и ту же группу должны быть однородными.

Для проверки на однородность для каждого из вычисляют величинуz-критерия 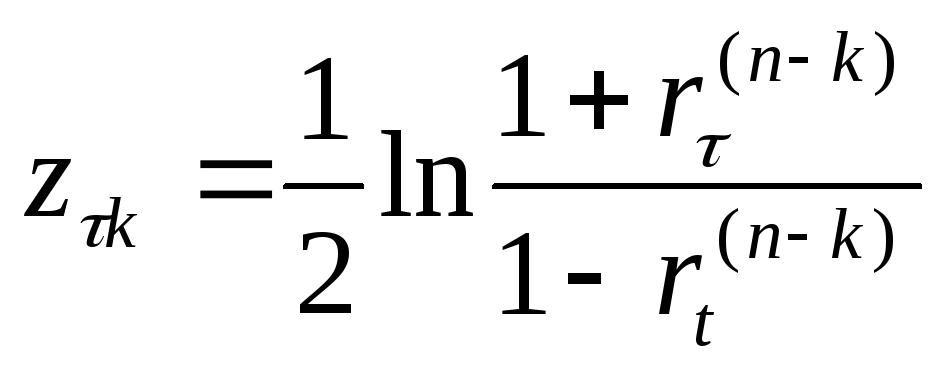, затем рассчитывают для каждой группы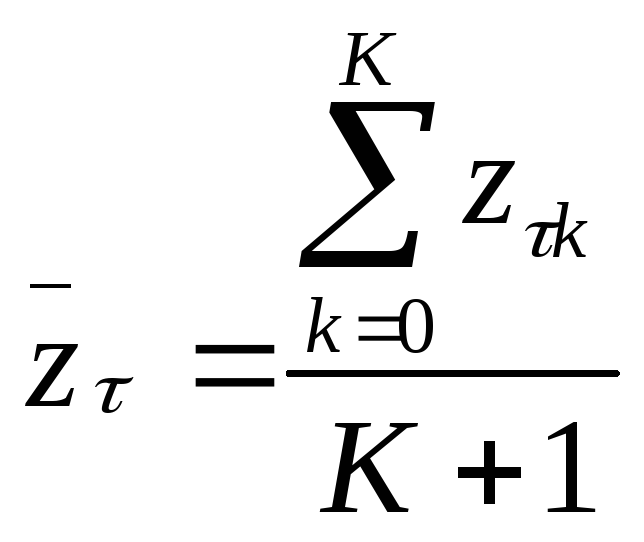. Далее для каждой группы рассчитывается значение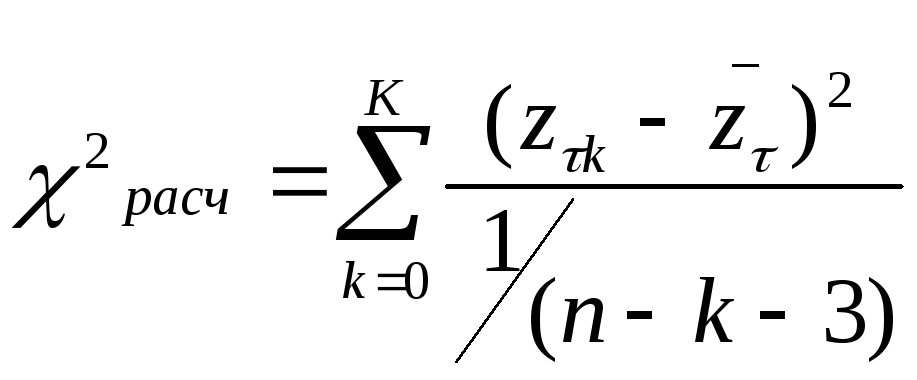, которое сравнивается табличным² (K).

Если ²_расч < ² (K), то гипотеза об однородности -й группы не отвергается. Если гипотеза об однородности не отвергается для всех групп, то можно принять, что автокорреляционная функция зависит не от начала отсчета, а только от разности t_i – t_j = , т.е. случайный компонент представляет собой стационарный в широком смысле случайный процесс.

Приведем результаты расчетов ²_расч .

	 = 1	 = 2	 = 3	 = 4	 = 5	 = 6	 = 7	2(0.05, 10)
2расч	0.714	0.039	0.08	0.054	0.541	0.269	0.575	18.3

Таким образом, можно предположить, что отклонения от линейного тренда являются стационарным в широком смысле случайным процессом.

Д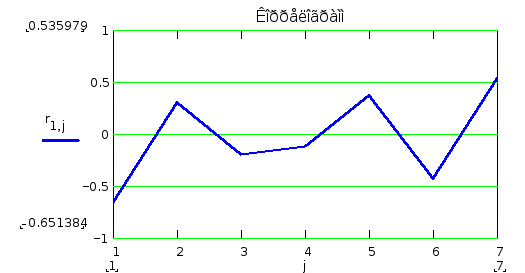ля наглядности построим коррелограмм, который в будущем может использоваться для выбора глубины авторегрессионной модели, тем самым можно увидеть как изменяется связь с прошлым.

Из анализа коррелограмма можно сделать о наличие некой циклической связи прошлых значений с настоящими.

2. Определение наличия автокорреляции в исходном ряду с

помощью критерия Дарбина-Уотсона.

REM: см. Приложение1

, где d_t = y_t - y_t^p. Из данной формулы с помощью преобразований можно получить, что DW[0;4]. Причем при DW = 0 – положительная автокорреляция, DW = 2 – нет автокорреляции, DW = 4 – отрицательная автокорреляция.

Полученное значение сравнивается с табличными верхним d_h и нижним d_l значениями, выбираемыми при уровне значимости , числе факторов в модели  и числе членов временного ряда n.

Могут иметь место следующие случаи:

DW < d_l – положительная автокорреляция;

d_h < DW < 4 - d_h – отсутствие автокорреляции;

DW > 4 – d_l – отрицательная автокорреляция;

d_l < DW < d_h или 4 - d_h < DW < 4 – d_l – нет статистических оснований принять или отвергнуть гипотезу об отсутствии автокорреляции.

В результате расчетов получили, что DW = 3.265; при  = 0.05,  = 1,

n = 30 - d_l = 1.35 , d_h = 1.39. Тогда 4 – d_l = 2.65, 4 – d_h = 2.61.

В рассматриваемом случае DW > 4 – d_l – отрицательная автокорреляция, поэтому можно переходить к построению авторегрессионной модели.